RadfordMathematics.com

Online Mathematics Book

Domain & Range of a Function

Given a function, \(f(x)\), there may be some values of \(x\) for which the function isn't well defined.
For instance, if we were asked to calculate the value of the function \(f(x) = \frac{2}{3x+6}\) when \(x = -2\) we would have some trouble.
Indeed, if we replace \(x\) by \(-2\) in the expression for \(f(x)\) we obtain: \[\begin{aligned} f(-2) & = \frac{2}{3\times (-2) + 6} \\ & = \frac{2}{-6+6} \\ f(-2) & = \frac{2}{0} \end{aligned} \] Since it is impossible to divide by zero, it is impossible to calculate the value of \(f(x)\) when \(x = -2\).
This highlights the importance of defining the domain of a function.

Example 2

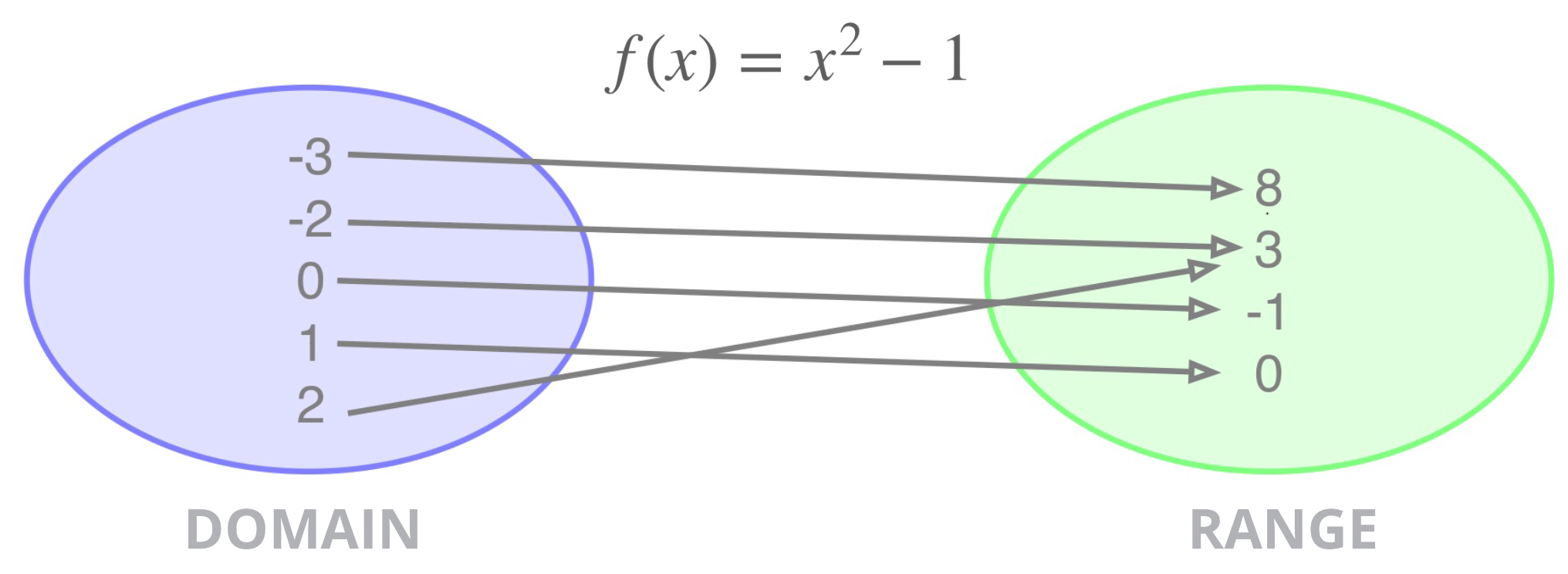
Consider the function \(f(x)=x^2-1\) for the following values of \(x\): \[-3,-2, 0, 1, 2\] \[\begin{aligned} f(-3) &= (-3)^2 - 1 \\ & = 9 - 1 \\ f(-3) &= 8 \end{aligned}\]

Calculating all of the other values of \(x\) this way we find:

  • For the input value \(x = -2\), the output value is: \[\begin{aligned} f(-2) &= (-2)^2 - 1 \\ & = 4 - 1 \\ f(-2) & = 3 \end{aligned}\] So \(-2\) maps onto \(3\)
  • For the input value \(x = 0\), the output value is: \[\begin{aligned} f(0) &= 0^2 - 1 \\ & = 0 - 1 \\ f(0) & = -1 \end{aligned}\] So \(0\) maps onto \(-1\)

  • For the input value \(x = 1\), the output value is: \[\begin{aligned} f(1) &= 1^2 - 1 \\ & = 1 - 1 \\ f(1) & = 0 \end{aligned}\] So \(1\) maps onto \(0\)
  • For the input value \(x = 2\), the output value is: \[\begin{aligned} f(2) &= 2^2 - 1 \\ & = 4 - 1 \\ f(2) & = 3 \end{aligned}\] So \(2\) maps onto \(3\)

Can be illustrated in a mapping diagram, as shown here:

Definition - Domain of a Function

Given a function, its domain is the set, or interval, of numbers for which the function is well defined and can be calculated.
For the function we saw in the introduction, \(f(x) = \frac{2}{3x+6}\), the domain would be all real numbers other than \(-2\).
We write this: \[\text{Domain} = \left \{ x \in \mathbb{R} | x \neq -2 \right \}\]

How to Find the Domain

To find a function's domain we should ask ourselves:

Are there any values of \(x\) at which this function can't be calculated (isn't well defined)?

To answer this question we must always remember:

  • Denominators cannot equal \(0\).

  • Expressions inside square roots (radicands) cannot be negative.
Once this question is answered then we can take the values of \(x\), at which the function isn't well defined, away from the set of real numbers \(\mathbb{R}\) to define the domain.

Must Know Examples

Example 1

Find the domain of the function defined as: \[f(x) = \frac{3}{2x-4}\]

Example 2

Find the domain of the function defined as: \[f(x) = 2\sqrt{x+3}\]

Example 3

Find the domain of the function defined as: \[f(x) = \frac{3}{x^2-4}\]

Example 4

Find the domain of the function defined as: \[f(x) = \frac{3}{\sqrt{2x+8}}\]

Tutorial

In the following tutorial we review the method for findng the formula for the \(n^{\text{th}}\) term of a linear sequence. Watch it now.

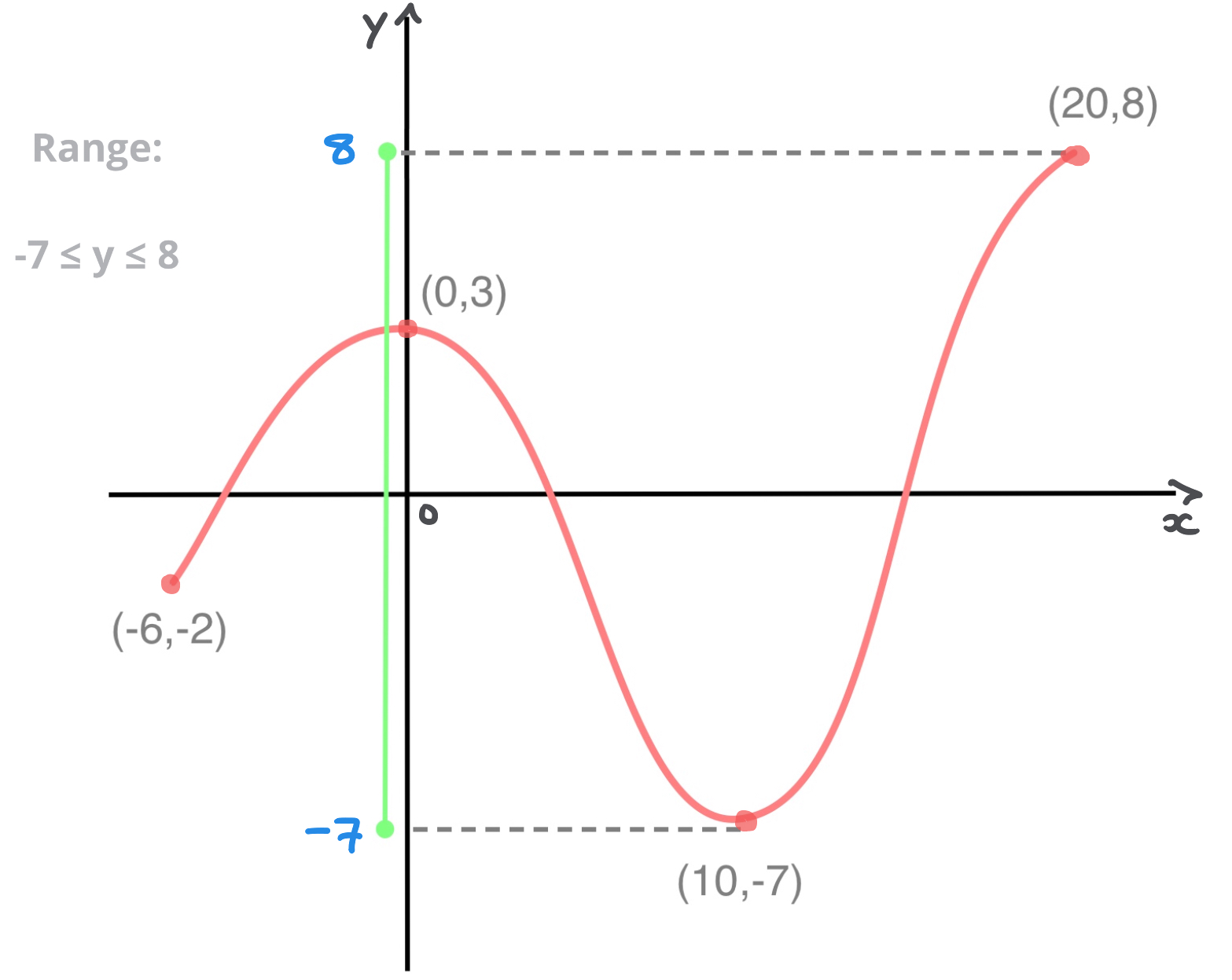
Reading Domain & Range from Graphs

Given a function \(f(x)\) and its curve \(y=f(x)\), we can read both the domain and range as follows:

  • The domain is the interval of \(x\) values seen when we project the curve on to the \(x\)-axis.
  • The range is the interval of \(y\) values seen when we project the curve on to the \(y\)-axis.
Each of these are illustrated in the example below.

Example

The following graph shows the curve of some function \(f(x)\):

Graph of \(y=f(x)\).

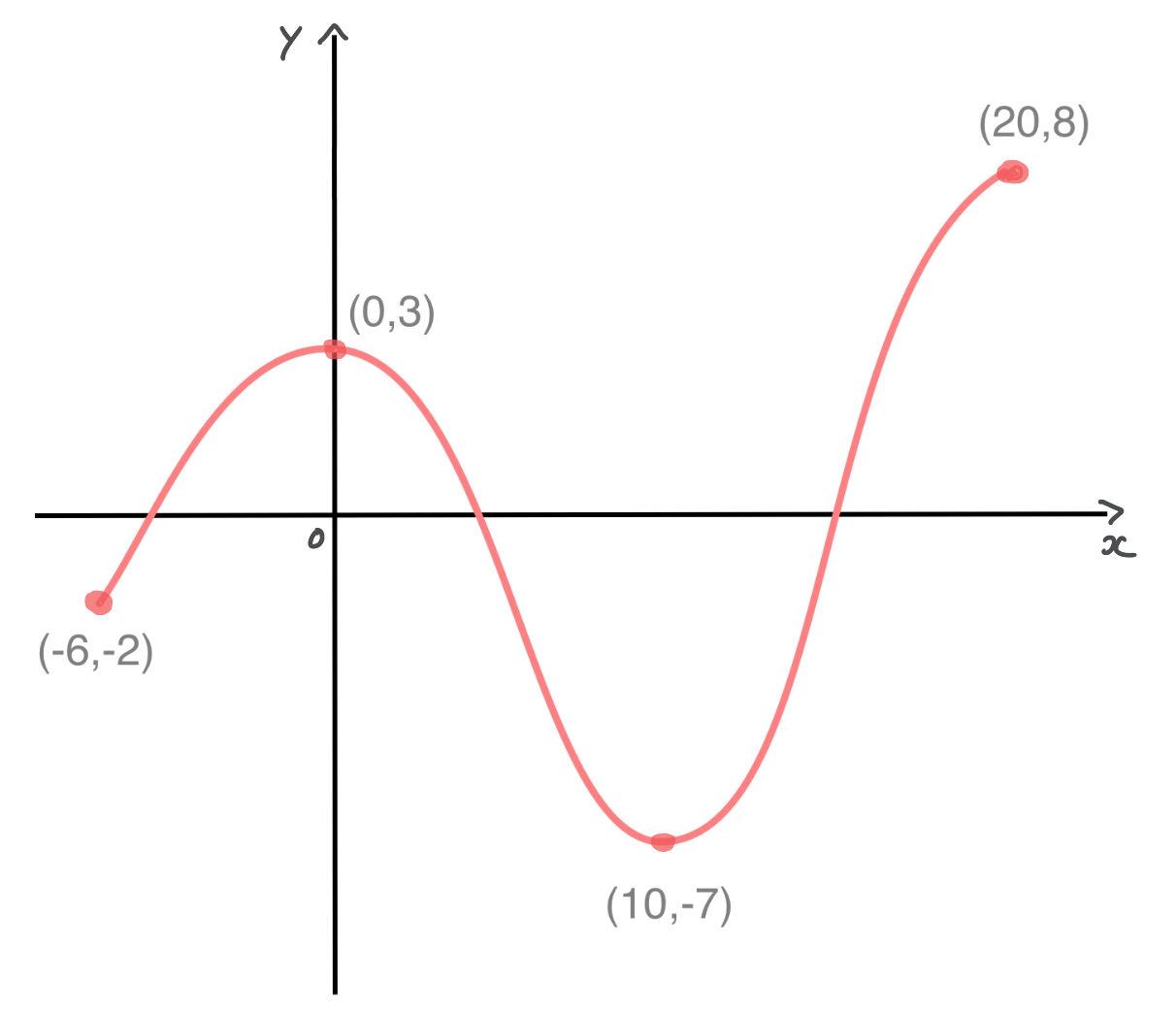
Using the graph, state:

  1. the domain
  2. the range.

Solution

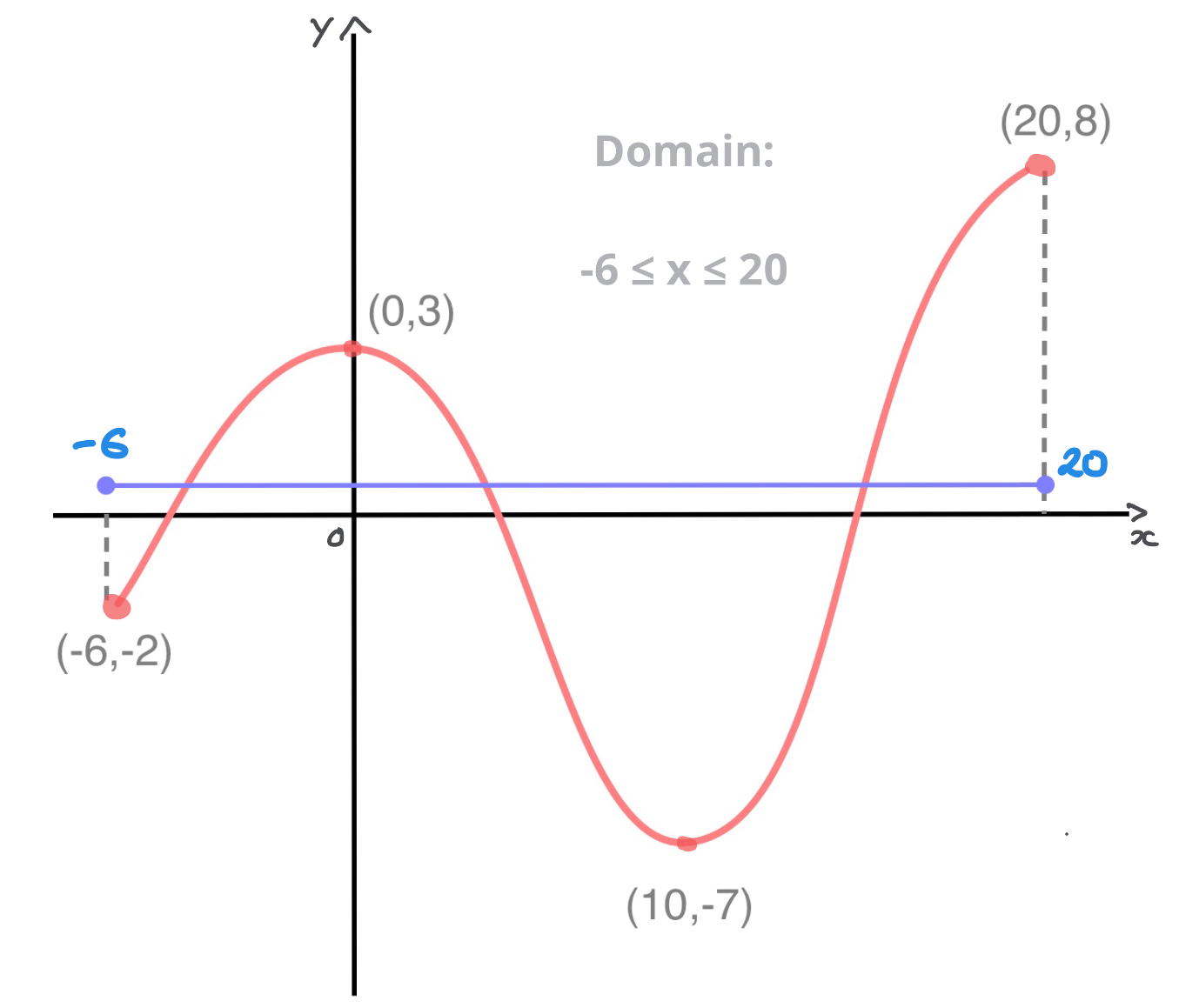
  1. To find the domain, we look at the interval of \(x\) values seen by projecting the curve onto the \(x\)-axis; this is done here in blue:
    We can see that the curve projects onto the interval: \[-6\leq x \leq 20\] More formally, we can now state that the domain is: \[\text{Domain} = \left \{ x \in \mathbb{R}| -6\leq x \leq 20 \right \}\]
  2. To find the range, we look at the interval of \(y\) values seen by projecting the curve onto the \(y\)-axis; this is done here in green:

Exercise

Find the domain of each of the following functions:

  1. \(f(x) = \frac{3}{2x-4}\)

  2. \(f(x) = \sqrt{x+5}\)

  3. \(f(x) = \sqrt{3x-9}\)

  4. \(f(x) = \frac{7}{9-x}\)

  5. \(f(x) = \frac{x}{x^2-4}\)

  6. \(f(x) = \frac{2x}{x^2+4}\)

Answers Without Working