RadfordMathematics.com

Standard Form - Part 1

(How to write a number in standard form)

The idea behind standard form is to write both very large and very small numbers in a convenient form. Here are a couple of examples of numbers written in standard form:

  • the distance from the Earth to the Sun is: \(149\ 600 \ 000 \ 000 \) m. In standard form this is written \(1.49 \times 10^{11}\) m.
  • The size of a Molecule of Oxygen is: \(0.000000000152\) m. In standard form this is written \(1.52 \times 10^{-10}\) m.
Writing numbers this way makes it much easier to see how big/small they are (as all we really have to focus on is how big/small the power of 10 is). Standard form also makes it much easier for us to compare two large (or small) numbers.

Tutorial 1: Writing Numbers in Standard Form

In this tutorial we learn how to write numbers in standard form. We do so by writing the three numbers:

  • \(273\ 000\ 000\)
  • \(0.0000273\)
  • \(4\ 050\)
in standard form.

Standard Form

When we write a number in standard form, we must write it in yje following way: \[a \times 10^k\] where the following two conditions must be met:

  • \(1 \leq a < 10\), the number \(a\) must be greater than, or equal to, \(1\) and must be less than \(10\).
  • \(k\in \mathbb{Z}\), in other words the power on \(10\) must be an integer: \(\mathbb{Z} = \left \{ \dots , -3, \ -2, \ -1, \ 0, \ 1, \ 2, \ 3, \ \dots \right \}\)

Exercise 1

Write each of the following numbers in standard form:

  1. \(3,240,000 \)
  2. \(0.0000123\)
  3. \(137,000\)
  4. \(0.0074\)
  5. \(607,000,000,000\)
  1. \(0.000000103\)
  2. \(9 \)
  3. \(0.67\)
  4. \(43,000\)
  5. \(0.00089\)
Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

Solution Without Working

We find the following results:

  1. \(3,240,000 = 3.24 \times 10^6\)
  2. \(0.0000123 = 1.23 \times 10^{-5}\)
  3. \(137,000 = 1.37 \times 10^5\)
  4. \(0.0074 = 7.4 \times 10^{-3}\)
  5. \(607,000,000,000 = 6.07 \times 1O^{11}\)
  6. \(0.000000103 = 1.03 \times 10^{-7}\)
  7. \(9 = 9\times 10^0 \)
  8. \(0.67 = 6.7\times 10^{-1}\)
  9. \(43,000 = 4.3\times 10^4\)
  10. \(0.00089 = 8.9 \times 10^{-4}\)

Rounding & Standard Form

When writing numbers in standard form, we usually round numbers to two or three significant figures. For instance, consider the number: \[2 \ 347 \ 128\] Without any rounding, writing this in standard form, leads to: \[2.347128\times 10^6\] This notation isn't practical. Instead, when writing numbers in standard form, we usually round to 2 or 3 significant figures, so that \(2.347128\times 10^6\) becomes:

  • \(2.3\times 10^6\) to two significant figures (2 sf)
  • \(2.35\times 10^6\) to three significant figures (3 sf)

Exercise 2

Writing all of your answers to three significant figures, write each of the following in standard form:

  1. \(278,120,001\)
  2. \(0.0004352617\)
  3. \(31,906,321,003\)
  4. \(0.000000789654\)
  5. \(301,888 \)
  1. \(0.010345\)
  2. \(978,909,456,001,745\)
  3. \(0.0050216\)
  4. \(8,927\)
  5. \(0.435269\)
Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 2

Solution Without Working

We find the following results:

  1. \(278,120,001 = 2.78 \times 10^6\)
  2. \(0.0004352617 = 4.35 \times 10^{-4}\)
  3. \(31,906,321,003 = 3.19\times 10^9\)
  4. \(0.000000789654 = 7.90 \times 10^{-7}\)
  5. \(301,888 =3.02 \times 10^5\)
  6. \(0.010345 = 1.03\times 10^{-2}\)
  7. \(978,909,456,001,745 = 9.79 \times 10^{14}\)
  8. \(0.0050216 = 5.02\times 10^{-3}\)
  9. \(8,927 = 8.93\times 10^3 \)
  10. \(0.435269 = 4.35\times 10^{-1}\)

Standard Form & Calculators

Although some calculators can present results in standard form, many use a slightly different notation to the one we have see here.

Calculators replace the number \(10\) by the letter \(E\)

Examples

Here are some examples of what a calculator can display and the number, in standard form, they are referring to.

Example 1

With your calculator, try calculating: \[987,654,321 \times 123,456,789\] You're likely to find: \[1.21933\text{E}17\] This means: \[1.21933\times 10^{17}\]

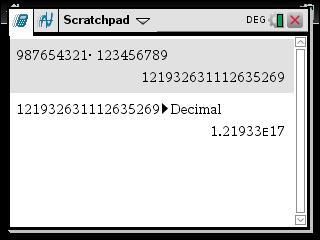
Notice that we had to convert the number in decimal form, via:

Menu > Number > Convert to Decimal
to see it written in standard form \(1.21933\text{E}17\)

Example 2

With your calculator, try calculating: \[5 \div 1234567890\] You're likely to see a result looking like: \[4.05\text{E}-9\] This means: \[4.05\times 10^{-9}\]

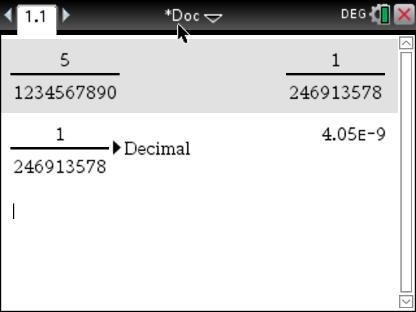
Notice that we had to convert the number in decimal form, via:

Menu > Number > Convert to Decimal
to see it written in standard form \(4.05\text{E}-9\)


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe to Our Channel

Subscribe Now and view all of our playlists & tutorials.