RadfordMathematics.com

Mid-Point of a Line Segment

We now learn how to calculate the coordinates of the mid-point of a line segment. The method and formula are clearly explained and illustrated with tutorials, worked examples as well as exercises with their answer keys.

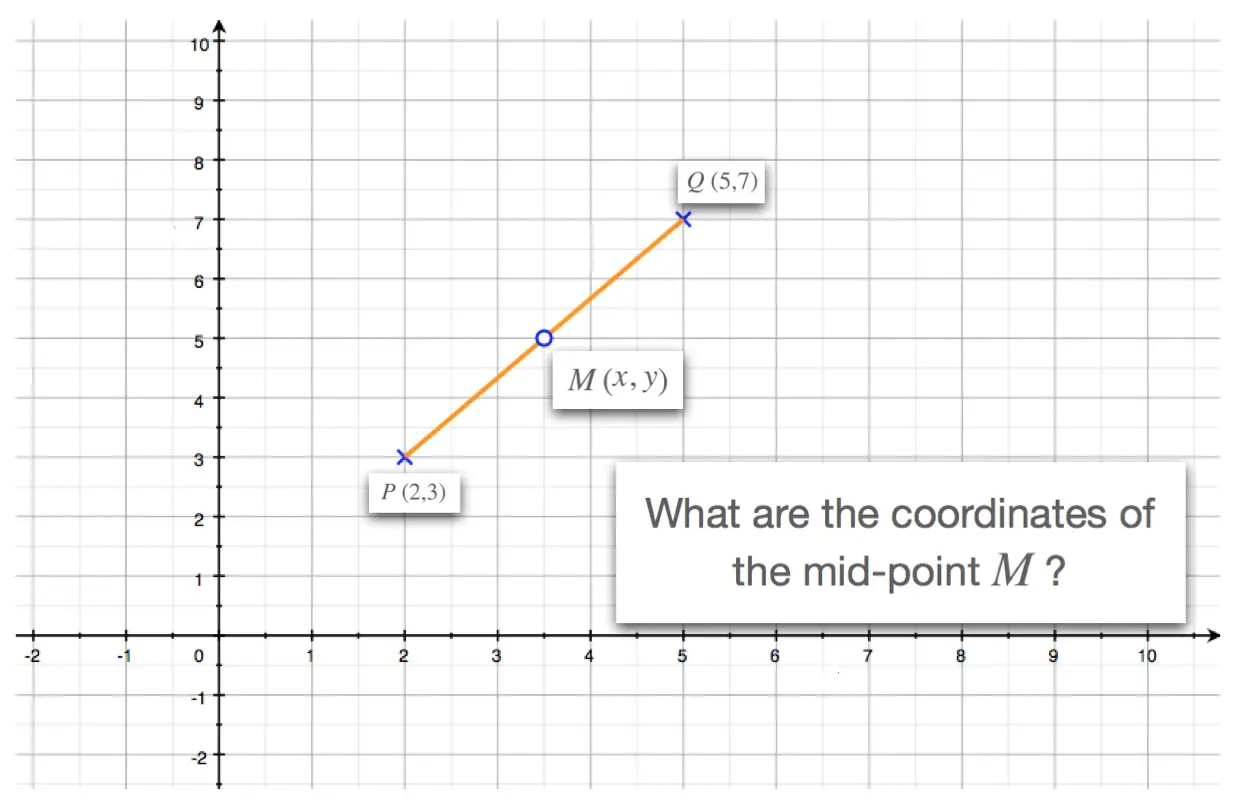For instance, we could be given the line segment \(PQ\), shown here and asked for the coordinates of its mid-point that we'll call \(M\).
With a bit of inspection we'd find that \(M\) has coordinates \(M\begin{pmatrix}3.5,5\end{pmatrix}\). But what if we weren't given a diagram? Or what if the end-points' coordinates weren't nice round numbers?
Then we'd need a formula to find the mid-point and that is what we learn here.

Tutorial 1: Formula for the Mid-Point of a Line Segment

In the following tutorial we learn/explain the formula and watch a worked example, showing how to use it.

Formula: Mid-Point of a Line Segment

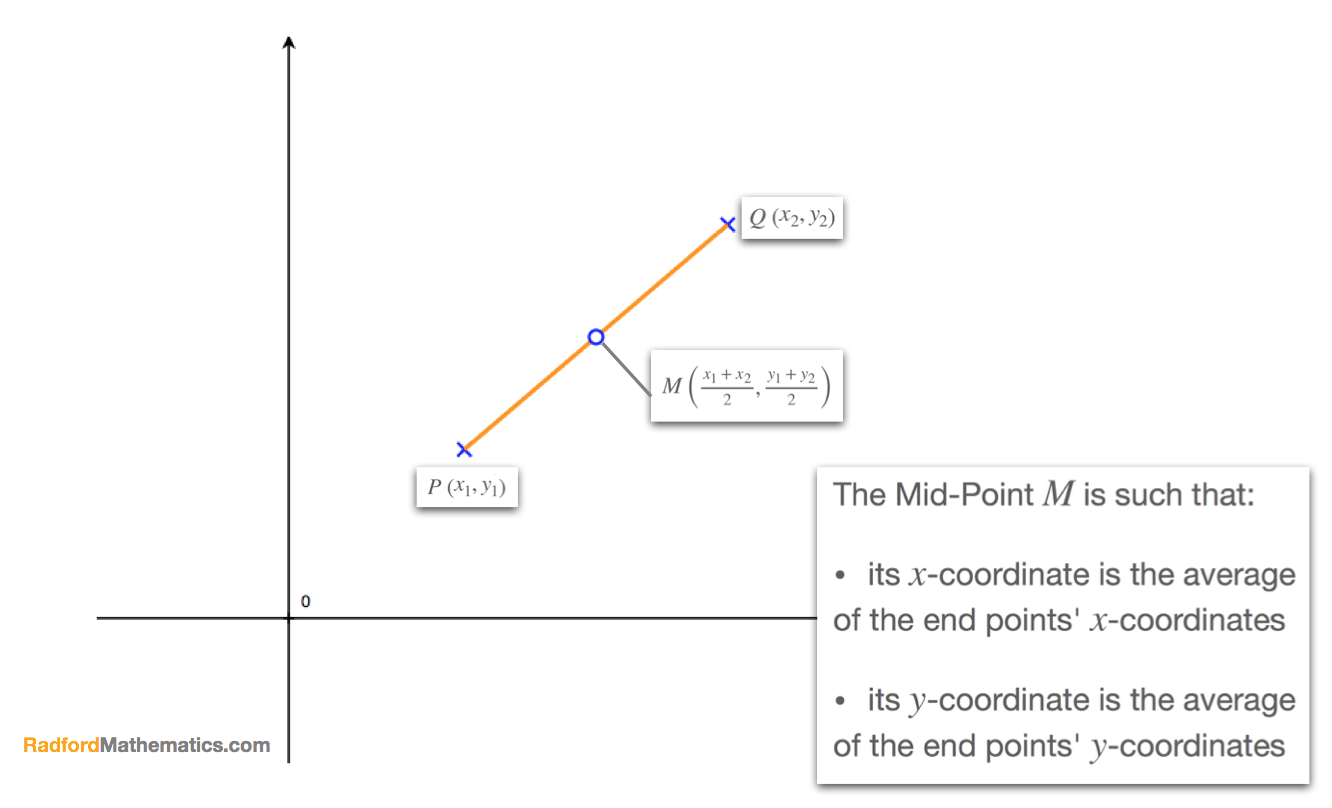
Given a line segment with end-points: \[P\begin{pmatrix}x_1,y_1\end{pmatrix} \quad \text{and} \quad Q\begin{pmatrix}x_2,y_2\end{pmatrix}\] its mid-point \(M\) has coordinates: \[M\begin{pmatrix}\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\end{pmatrix}\] Put "simply", the mid-point is such that:

  • its \(x\)-coordinate is the average of the end points' \(x\)-coordinates
  • its \(y\)-coordinate is the average of the end points' \(y\)-coordinates

This formula is further illustrated in the diagram shown here for the line segment with end-points \(P\begin{pmatrix}x_1,y_1\end{pmatrix}\) and \(Q\begin{pmatrix}x_2,y_2\end{pmatrix}\).

Exercise 1

Calculate the coordinates of each of the following line segments:

  1. \(PQ\) with end-points \(P\begin{pmatrix}-2,-3\end{pmatrix}\) and \(Q\begin{pmatrix}4,7\end{pmatrix}\).
  2. \(AB\) with end-points \(A\begin{pmatrix}-5,8\end{pmatrix}\) and \(B\begin{pmatrix}3,-4\end{pmatrix}\).
  3. \(ST\) with end-points \(S\begin{pmatrix}0,0\end{pmatrix}\) and \(T\begin{pmatrix}4,6\end{pmatrix}\).
  4. \(AB\) with end-points \(A\begin{pmatrix}-1,-4\end{pmatrix}\) and \(B\begin{pmatrix}4,2\end{pmatrix}\).
  5. \(UV\) with end-points \(U\begin{pmatrix}2,1\end{pmatrix}\) and \(V\begin{pmatrix}9,6\end{pmatrix}\).
  6. \(AB\) with end-points \(A\begin{pmatrix}-5,8\end{pmatrix}\) and \(B\begin{pmatrix}4,-5\end{pmatrix}\).

Note: this exercise can be downloaded as a worksheet to practice with: worksheet

Answers Without Working

  1. We find \(M\begin{pmatrix}1,\ 2 \end{pmatrix}\)
  2. We find \(M\begin{pmatrix}-1,\ 2 \end{pmatrix}\)
  3. We find \(M\begin{pmatrix}2,\ 3 \end{pmatrix}\)
  4. We find \(M\begin{pmatrix} \frac{3}{2},\ -1 \end{pmatrix}\), which can also be written \(M\begin{pmatrix} 1.5,\ -1 \end{pmatrix}\)
  5. We find \(M\begin{pmatrix} \frac{11}{2},\ \frac{7}{2} \end{pmatrix}\), which can also be written \(M\begin{pmatrix} 5.5,\ 3.5 \end{pmatrix}\)
  6. We find \(M\begin{pmatrix} -\frac{1}{2},\ \frac{3}{2} \end{pmatrix}\), which can also be written \(M\begin{pmatrix} -0.5,\ 1.5 \end{pmatrix}\)

Exam-Style Question

We now learn how to solve a well-known exam-type question. We'll definitely want to know how to solve this as it is frequent in exams.

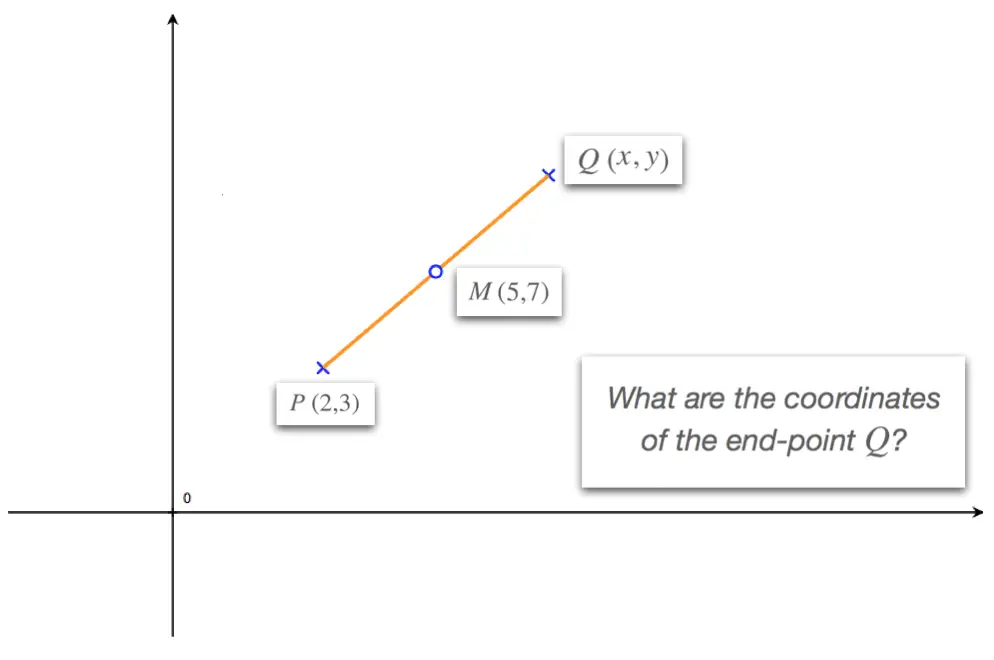The scenario that we're faced with is summarized in three bullet points:

  • We know the coordinates of one of the segment's end-points
  • We know the coordinates of the segment's mid-point
  • We need to find the coordinates of the segment's other end-points.
This scenario is illustrated in the diagram we see here. We're given the coordinates of the end-point \(P\) as well as the coordinates of the mid-point \(M\) and we need to find the coordinates of the end-point \(Q\).

We learn two ways for solving this type of problem. Each of these is explained in the two tutorials, below (each tutorial shows one of the methods).

Tutorial 2

In this tutorial we learn a method for finding the unknown end-point, which is the more intuitive of the two methods we'll learn.

Tutorial 3

In this tutorial we learn how to find the unknown end-point by rearranging the mid-point formula, we saw above, remember that was the coordinates of the mid-point \(M\) are: \[M\begin{pmatrix} \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} \end{pmatrix}\] Exam questions are sometimes written in such a way to "push" us towards moving this method, so it's definitely worth knowing.

Exercise 2

Using either of the methods, shown above, answer each of the following:

  1. A line segment \(AB\) has an end-point \(A\begin{pmatrix}-2,-3\end{pmatrix}\) and its mid-point has coordinates \(M\begin{pmatrix}1,5\end{pmatrix}\).
    Find the coordinates of the segment's other end-point \(B\).
  2. A line segment \(PQ\) has an end-point \(P\begin{pmatrix}3,5\end{pmatrix}\) and its mid-point has coordinates \(M\begin{pmatrix}-1,2\end{pmatrix}\).
    Find the coordinates of the segment's other end-point \(Q\).
  3. A line segment \(ST\) has an end-point \(S\begin{pmatrix}-2,-4\end{pmatrix}\) and its mid-point has coordinates \(M\begin{pmatrix}2,-3\end{pmatrix}\).
    Find the coordinates of the segment's other end-point \(T\).
  4. A line segment \(PQ\) has an end-point \(P\begin{pmatrix}-3,4\end{pmatrix}\) and its mid-point has coordinates \(M\begin{pmatrix}2,-1\end{pmatrix}\).
    Find the coordinates of the segment's other end-point \(Q\).
  5. A line segment \(AB\) has an end-point \(A\begin{pmatrix}1,-3\end{pmatrix}\) and its mid-point has coordinates \(M\begin{pmatrix}5,2\end{pmatrix}\).
    Find the coordinates of the segment's other end-point \(B\).

Note: this exercise can be downloaded as a worksheet to practice with: worksheet

Answers Without Working

  1. We find \(B\begin{pmatrix}4,13\end{pmatrix}\).
  2. We find \(Q\begin{pmatrix}-5,-1\end{pmatrix}\).
  3. We find \(T\begin{pmatrix}6,-2\end{pmatrix}\).
  4. We find \(Q\begin{pmatrix}7,-6\end{pmatrix}\).
  5. We find \(B\begin{pmatrix}9,7\end{pmatrix}\).


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe to Our Channel

Subscribe Now and view all of our playlists & tutorials.