RadfordMathematics.com

How to Find a Line's Equation

(given two points through which it passes)

We'll often need to find the equation of a line given two points it passes through.

For instance, we may be asked to find the equation of the line passing through the points:

\(\begin{pmatrix}1,-2\end{pmatrix}\) and \(\begin{pmatrix}4,4\end{pmatrix}\).

Remember that the equation of a line is written: \[y = mx+c\] Where:

  • \(m\) is the gradient (also called slope) it equals the amount the line goes-up (or down if \(m<0\)) for each unit-step in the positive \(x\) direction.
  • \(c\) is the \(y\)-intercept. Its value equals to the \(y\)-coordinate of the point at which the line crosses/cuts the \(y\)-axis.

To learn how to find a line's equation, the method is explained in a step-by-step tutorial. The method is then written for us and a detailed example given.
Finally, we work our way through a practice exercise for which each solution is explained in a video tutorial.

Tutorial 1

Method 1: finding the equation of a line

Given two points with coordinates:

\(\begin{pmatrix} x_1,y_1\end{pmatrix}\) and \(\begin{pmatrix} x_2,y_2\end{pmatrix}\)
we find its line equation in two steps:
  • Step 1: calculate the gradient \(m\) using the gradient formula: \[m = \frac{y_2-y_1}{x_2-x_1}\]
  • Step 2: find the \(y\)-intercept \(c\).
    Do this substituting the coordinates of either of the two points we have, \(\begin{pmatrix} x_1,y_1\end{pmatrix}\) or \(\begin{pmatrix} x_2,y_2\end{pmatrix}\), into the line equation \(y=mx+c\) and solving for \(c\).

Example

Find the equation of the line passing through the two points:

\(\begin{pmatrix} - 1, -5 \end{pmatrix}\) and \(\begin{pmatrix}4,5 \end{pmatrix}\).

Solution

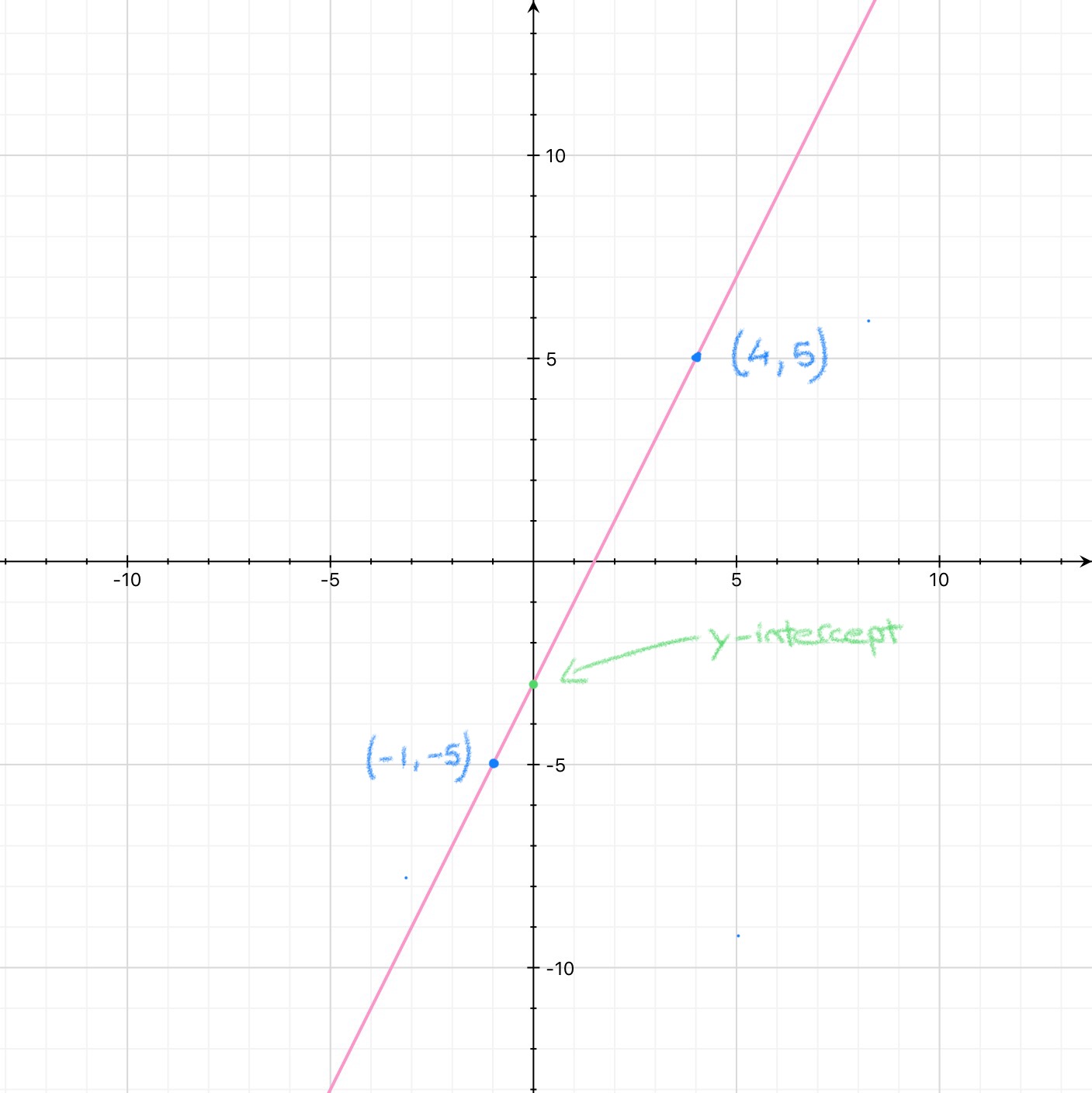
Looking at the line passing through the two points \(\begin{pmatrix} - 1, -5 \end{pmatrix}\) and \(\begin{pmatrix}4,5 \end{pmatrix}\), we can see that the line is going upwards, as we go from left to right, this tells us that the gradient we're looking for should be positive!

We can also see that the \(y\)-intercept seems to equal to \(3\).

We now use our two-step method to find this line's equation:

  • Step 1: find the gradient, using the gradient formula: \[m = \frac{y_2 - y_1}{x_2 - x_1}\]



    If we call point \(1\) the point \(\begin{pmatrix}-1,-5\end{pmatrix}\), then \(x_1 = -1\) and \(y_1 = -5\) and calling point \(2\) the point \(\begin{pmatrix} 4,5\end{pmatrix}\) so that \(x_2 = 4\) and \(y_2 = 5\), then the formula becomes: \[\begin{aligned} m & = \frac{y_2 - y_1}{x_2 - x_1} \\ & = \frac{5 - (-5)}{4 - (-1)} \\ & = \frac{5+5}{4+1} \\ & = \frac{10}{5} \\ m & = 2 \end{aligned}\] Since the gradient is \(m=2\), at this stage we can state that the equation must look something like: \[y = 2x+c\] All we need to find now is the \(y\)-intercept \(c\).
  • Step 2: find the \(y\)-intercept \(c\).
    To do this we choose either of the two points, \(\begin{pmatrix} - 1, -5 \end{pmatrix}\) or \(\begin{pmatrix}4,5 \end{pmatrix}\) (it doesn't matter which one) and plug its coordinates into the line equation \(y=mx+c\).
    Let's say we choose the point \(\begin{pmatrix}4,5 \end{pmatrix}\) then we replace \(x\) by \(4\) and \(y\) by \(5\) in the line equation \(y=2x+c\).

    That's: \[5 = 2\times 4 + c\] We now rearrange this equation to find \(c\): \[\begin{aligned} & 5 = 2\times 4 + c \\ & 5 = 8 + c \\ & 5 - 8 = c \\ & - 3 = c \\ & c = -3 \end{aligned}\] Now that we know the value of \(c\), we can state the line equation: \[y = 2x - 3\]

Exercise

  1. Consider the two points \(\begin{pmatrix}2,-4\end{pmatrix}\) and \(\begin{pmatrix}7,6\end{pmatrix}\).
    1. Draw the line passing through these two points.
    2. Find the gradient of the line passing through these two points.
    3. Find the \(y\)-intercept of the line and state the line's equation.

  2. Consider the two points \(\begin{pmatrix}-1, 5\end{pmatrix}\) and \(\begin{pmatrix}3, 1\end{pmatrix}\).
    1. Draw the line passing through these two points.
    2. Find the gradient of the line passing through these two points.
    3. Find the \(y\)-intercept of the line and state the line's equation.

  3. Consider the two points \(\begin{pmatrix}-1, -4\end{pmatrix}\) and \(\begin{pmatrix}2, 5\end{pmatrix}\).
    1. Draw the line passing through these two points.
    2. Find the gradient of the line passing through these two points.
    3. Find the \(y\)-intercept of the line and state the line's equation.

  4. Find the equation of the line passing through the two points \(\begin{pmatrix}-2,6\end{pmatrix}\) and \(\begin{pmatrix} 3,1\end{pmatrix}\).

  5. Find he equation of the line passing through the two points \(\begin{pmatrix}-3,-5\end{pmatrix}\) and \(\begin{pmatrix} 1, 7 \end{pmatrix}\).

Answers Without Working

    2. The gradient is \(m=2\).
    3. The \(y\)-intercept is \(c = -8\) and the line's equation is: \[y = 2x - 8\]

    2. The gradient is \(m = -1\).
    3. The \(y\)-intercept is \(c = 4\) and the line's equation is: \[y = -x+4\]

    2. The gradient is \( m = 3\).
    3. The \(y\)-intercept is \(c = -1\) and the line's equation is: \[ y = 3x - 1\]

  4. The line's equation is \(y = -x+4\)
  5. The line's equation is \(y = 3x+4\)

Tutorial 2

Method 2: finding the equation of a line

Given two points with coordinates:

\(\begin{pmatrix} x_1,y_1\end{pmatrix}\) and \(\begin{pmatrix} x_2,y_2\end{pmatrix}\)
we find its line equation in two steps:
  • Step 1: calculate the gradient \(m\) using the gradient formula: \[m = \frac{y_2-y_1}{x_2-x_1}\]
  • Step 2: find the \(y\)-interept.
    Do this by making \(y\) the subject in either: \[y - y_1 = m\begin{pmatrix}x - x_1 \end{pmatrix}\] or \[y - y_2 = m\begin{pmatrix}x - x_2 \end{pmatrix}\] which ever one you choose does not matter.

Exercise 2

  1. Consider the points \(\begin{pmatrix}0,12\end{pmatrix}\) and \(\begin{pmatrix}5,-3\end{pmatrix}\).
    1. Plot these two points on an \(xy\) grid and draw the line passing through these two points.
    2. Find the equation of the line passing through these two points.

  2. Consider the points \(\begin{pmatrix}-8,-4\end{pmatrix}\) and \(\begin{pmatrix}-2,8\end{pmatrix}\).
    1. Plot these two points on an \(xy\) grid and draw the line passing through these two points.
    2. Find the equation of the line passing through these two points.

  3. Consider the points \(\begin{pmatrix}-1,-1\end{pmatrix}\) and \(\begin{pmatrix}1,5\end{pmatrix}\).
    1. Plot these two points on an \(xy\) grid and draw the line passing through these two points.
    2. Find the equation of the line passing through these two points.

  4. Consider the points \(\begin{pmatrix}-6,1\end{pmatrix}\) and \(\begin{pmatrix}2,5\end{pmatrix}\).
    1. Plot these two points on an \(xy\) grid and draw the line passing through these two points.
    2. Find the equation of the line passing through these two points.

Answers Without Working

    2. This line's equation is \(y = -3x+12\)

    2. This line's equation is \(y = 2x+12\)

    2. This line's equation is \(y = 3x+2\)

    2. This line's equation is \(y = \frac{x}{2}+4\), which can also be written \(y = 0.5x + 4\).

    2. This line's equation is \(y = 4x\)