RadfordMathematics.com

Factoring Polynomials

(Writing Polynomials in Factored Form, in \(\mathbb{R}\))

We now learn how to factor polynomials, that is how to write polynomial functions in factored form. We learn how to do this within the set of real numbers, \(\mathbb{R}\).

So by the end of this section we’ll understand why the polynomial defined as: \[f(x) = 2x^3 - 4x^2 - 10x + 12\] Can be written, in factored form, as: \[f(x) = 2(x - 1)(x + 2)(x - 3)\] Note: if you‘re working within the set of complex numbers, \(\mathbb{C}\), then once you are done reading this section move-on to the Fundamental Theorem of Algebra (FTA).

The following graph shows the curve: \[y = 2x^3 - 4x^2 - 10x + 12\]

Important Property

A polynomial function, \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\), of degree \(n\), it can have up to \(n\) zeros (roots) in \(\mathbb{R}\).

So for instance:

  • A quadratic \(f(x) = ax^2 + bx + c\) can have up to two real zeros.
  • A cubic \(f(x) = ax^3 + bx^2 + cx + d\) can have up to three real zeros.
  • A quartic \(f(x) = ax^4+ bx^3 + cx^2 + dx + e\) can have up to four real zeros.

Root Factoring Polynomials

If a polynomial, \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\), has \(n\) real zeros (real roots) \(c_1\), \(c_2\), ... \(c_n\) then it can be written, in factored form, as the product of \(n\) linear factors: \[f(x)=a_n.\begin{pmatrix}x - c_1 \end{pmatrix}.\begin{pmatrix}x - c_2 \end{pmatrix} \dots \begin{pmatrix}x - c_n \end{pmatrix}\] If it has less than \(n\) zeros, say \(m\) zeros \(c_1\), \(c_2\), ... \(c_m\), \(m < n \), then in factored form it can be written as a product of \(m\) linear factores and a quotient polynomial \(Q(x)\): \[f(x)=\begin{pmatrix}x - c_1 \end{pmatrix}.\begin{pmatrix}x - c_2 \end{pmatrix} \dots \begin{pmatrix}x - c_m \end{pmatrix}.Q(x)\] where \(Q(x)\), the quotient polynomial, can be found by dividing \(f(x)\) by the product of all the linear factors: \[Q(x) = \frac{f(x)}{\begin{pmatrix}x - c_1 \end{pmatrix}.\begin{pmatrix}x - c_2 \end{pmatrix} \dots \begin{pmatrix}x - c_m \end{pmatrix}}\]

What this means (and enables us to do)

Given a polynomial, to write it in factored form we need to find its zeros, also called roots.

Once we have the zeros, the factor theorem allows us to state that each of the zeros of \(f(x)\), those are numbers \(c_1\), \(c_2\), ... such that \(f(c_1)=0\), \(f(c_2) = 0\), ... , allows us to define a linear factor of \(f(x)\): \[\begin{pmatrix}x-c_1\end{pmatrix}, \ \begin{pmatrix}x-c_1\end{pmatrix}, \ \dots \] So for example, if the cubic polynomial: \[f(x) = 2x^3 - 4x^2 - 10x + 12\] has three zeros: \(-2\), \(1\) and \(3\), it can be written in factored form as: \[f(x) = 2.\begin{pmatrix}x+2\end{pmatrix}\begin{pmatrix}x-1\end{pmatrix}\begin{pmatrix}x-3\end{pmatrix}\] where the \(2\) at the front is the polynomial's leading coefficient.

Using a Polynomial's Graph to Factor it

To factor a polynomial \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1 + a_0\) we can use our calculator to plot the curve: \[y = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1 + a_0\] The zeros are then all of the values of \(x\) at which the curve cuts the \(x\)-axis, which we can find with the "zero" function on the calculator.

Example 1

The curve we see here is the curve of the cubic polynomial: \[f(x) = 2x^3 - 6x^2 - 2x + 6\] We can see that it cuts the \(x\)-axis at: \[\left \{ -1, \ 2, \ 3 \right \}\] those are all the zeros of this cubic polynomial, \[f(x) = 2 \begin{pmatrix}x + 1 \end{pmatrix}.\begin{pmatrix}x - 1 \end{pmatrix}.\begin{pmatrix}x - 1 \end{pmatrix}\]


\[y = 2x^3 - 6x^2 - 2x + 6\]

Example 2

\[y = 2x^3 - 6x^2+8\]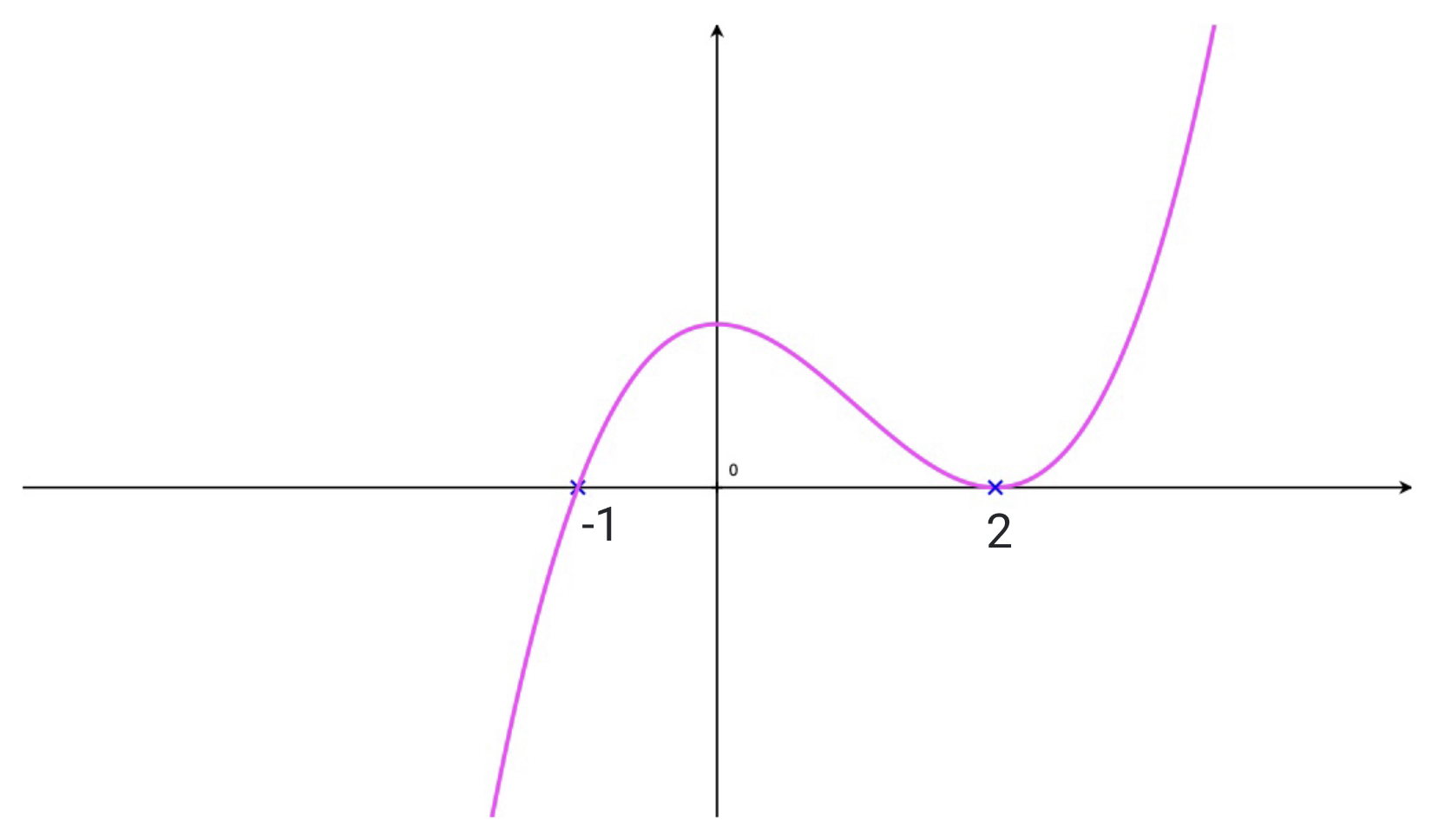
The curve we see here is the curve of the cubic polynomial: \[f(x) = 2x^3 - 6x^2+8\] We can see that it cuts the \(x\)-axis at: \[x = -1\] and that it touches the \(x\)-axis at: \[x = 2\] When a polynomial touches the \(x\)-axis like it does here at \(x = 2\) we say it has multiplicty. those are all the zeros of this cubic polynomial, \[f(x) = 2 \begin{pmatrix}x + 1 \end{pmatrix}.\begin{pmatrix}x - 2 \end{pmatrix}^2\]

Example 3

The curve we see here is the curve of the cubic polynomial: \[f(x) = 3x^3 - 3x^2 + 12x- 12\] We can see that it only cuts the \(x\)-axis once at: \[x = 1\] this is this polynomial's only zero and so in factored form it is written: \[f(x) = 3\begin{pmatrix}x - 1 \end{pmatrix}.\begin{pmatrix}x^2 + 4 \end{pmatrix}\] Notice that the quotient polynomial is of degree 2, indeed \(Q(x = x^2 + 4\).

\[y = 3x^3 - 3x^2 + 12x- 12\]

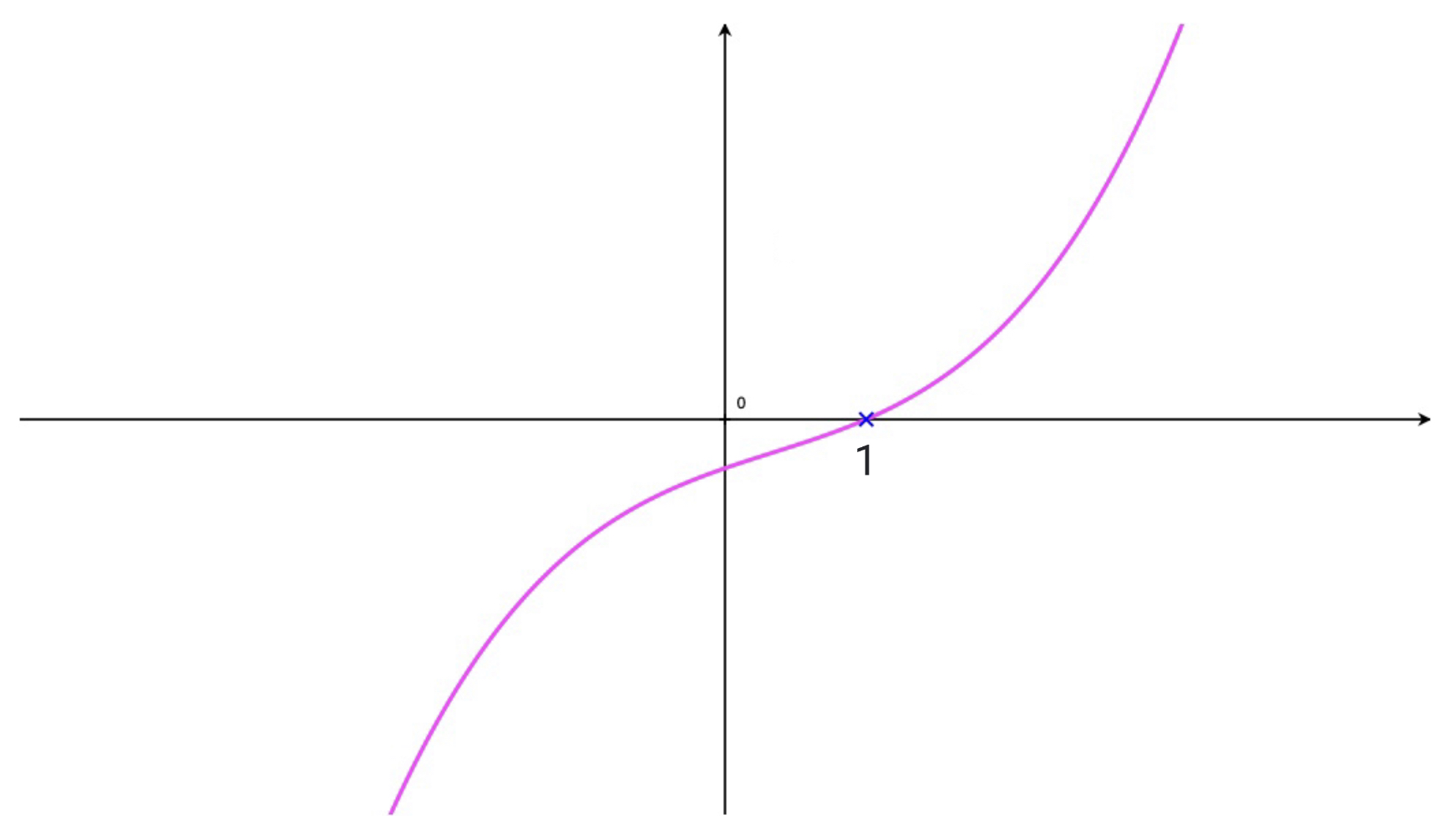
Multiplicity of Roots (of Zeros)

In Example 3, above, we said that the zero at \(x = 2\) had multiplicity. In fact, we say that it has a multiplicity of 2.

Tutorial: Remainder Theorem for Polynomials

In this tutorial, we learn the remainder theorem for polynomials. We start by stating the theorem, we then illustrate how it can be used alongside Horner's Method for evaluating polynomials, to quickly find the remainder when dividing the polynomial

Factor Theorem for Polynomials

Given a polynomial function, \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\), and a number \(c\) (real or complex) the factor theorem states that \(f(c) = 0\) if and only if \(x-c\) is a factor of \(f(x)\).

Using the remainder theorem t

What this means (and enables us to do)

The factor theorem provides us with a method for factoring polynomials. Indeed, if we know that a number \(c\) is a zero of a polynomial \(f(x)\), that is if: \[f(c) = 0\] then the factor theorem tells us that \(\begin{pmatrix}x - c \end{pmatrix}\) is factor of \(f(x)\). This means that there must be a quotient function, \(Q(x)\), such that: \[f(x) = \begin{pmatrix}x - c \end{pmatrix}.Q(x)\] The quotient function, \(Q(x)\), can be found using synthetic division of polynomials.

In turn, since the quotient function \(Q(x)\) is also a polynomial function we can look for its zeros and factor it further.

Important Note: a polynomial of degree \(n\) can have upto \(n\) zeros and therefore upto \(n\) factors of the type \(x-c\).

Exercise 1

List all of the possible rational zeros for each of the following polynomials:

  1. \(f(x) = x^3 - 7x^2 + 7x + 15\)
  2. \(f(x) = x^4 - 4x^3 - 13x^2 + 4x + 12\)
  3. \(f(x) = x^5 - 3x^4 + 7x^2 + 10\)
  4. \(f(x) = 2x^3 - 6x^2 + 5x - 8\)
  5. \(f(x) = 6x^3 - 11x^2 - 7x + 10\)
  6. \(f(x) = 3x^6 - 4x^5 + 2x^4 - 3x + 12\)
  7. \(f(x) = -2x^3 + 9x^2 +6x - 5\)
  8. \(f(x) = 4x^4 - 20x^3 - 60x^2 + 20x + 56\)

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

Solution Without Working

  1. For \(f(x) = x^3 - 7x^2 + 7x + 15\), the possible rational roots are: \[\left \{ \pm 1, \ \pm 3, \ \pm 5, \ \pm 15 \right \}\]
  2. For \(f(x) = x^4 - 4x^3 - 13x^2 + 4x + 12\), the possible rational roots are: \[\left \{ \pm 1, \ , \ \pm 2, \ \pm 3, \ \pm 4, \ \pm 6, \ \pm 12 \right \}\]
  3. For \(f(x) = x^5 - 3x^4 + 7x^2 + 10\), the possible rational roots are: \[\left \{ \pm 1, \ \pm 2, \ \pm 5, \ \pm 10 \right \}\]
  4. For \(f(x) = 2x^3 - 6x^2 + 5x - 8\), the possible rational roots are: \[\left \{ \pm \frac{1}{2}, \ \pm 1, \ \pm 2, \ \pm 4, \ \pm 8 \right \}\]
  5. For \(f(x) = 6x^3 - 11x^2 - 7x + 10\), the possible rational roots are: \[\left \{ \pm \frac{1}{6}, \ \pm \frac{1}{3}, \ \pm \frac{1}{2}, \ \pm \frac{2}{3}, \ \pm \frac{5}{6}, \ \pm 1, \ \pm \frac{5}{3}, \ \pm 2, \ \pm \frac{5}{2}, \ \pm \frac{10}{3}, \ \pm 5, \ \pm 10 \right \}\]
  6. For \(f(x) = 3x^6 - 4x^5 + 2x^4 - 3x + 12\), the possible rational roots are: \[\left \{ \pm \frac{1}{3}, \ \pm \frac{2}{3}, \ \pm 1, \ \pm \frac{4}{3}, \ \pm 2, \ \pm 5, \ \pm 10 \right \}\]
  7. For \(f(x) = -2x^3 + 9x^2 +6x - 5\), the possible rational roots are: \[\left \{ \pm \frac{1}{2}, \ \pm 1, \ \pm \frac{5}{2}, \ \pm 5 \right \}\]
  8. For \(f(x) = 4x^4 - 20x^3 - 60x^2 + 20x + 56\), the possible rational roots are: \[\left \{ \pm \frac{1}{4} , \ \pm \frac{1}{2}, \ \pm 1, \ \pm 2, \ \pm 4, \ \pm 8, \ \pm 14, \ \pm 28, \ \pm 56 \right \}\]

Exercise 2

Using the factor theorem answer each of the following:

  1. Show that \(\begin{pmatrix}x+1 \end{pmatrix}\) is a factor of \(f(x) = 2x^4 - x^3 - 2x^2 - 4x - 5\).
  2. Is \(\begin{pmatrix}x - 2 \end{pmatrix}\) a factor of \(f(x) = 3x^3 - 5x^2 + 4x - 12\)? Justify your answer.
  3. Is \(\begin{pmatrix}x + 3 \end{pmatrix}\) a factor of \(f(x) = -x^3 + x^2 + 11x - 1\)? Justify your answer.
  4. Show that \(\begin{pmatrix}x - \frac{1}{2}\end{pmatrix}\) is a factor of \(f(x) = 4x^5 - 2x^4 - 8x^3 + 16x^2 - 12x + 3\).
  5. Given \(\begin{pmatrix}x-2\end{pmatrix}\) is a factor of \(f(x) = x^3 - 5x^2 + px - 10\), find the value of \(p\).

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 2

Solution Without Working

  1. For \(f(x) = x^3 - 2x^2 - 5x + 6\), we find the following zeros: \[\left \{ -2, \ 1, \ 3 \right \}\]
  2. For \(f(x) = 5x^3 + 8x^2 - 79x + 30\), we find the zeros: \[\left \{ -5, \ \frac{2}{5}, \ 3 \right \}\]
  3. For \(f(x) = 3x^3 + x^2 - 12x - 4\), we find the following roots (zeros): \[\left \{ -2, \ - \frac{1}{3}, \ 2 \right \}\]
  4. For \(f(x) = x^4 - x^3 - 19x^2 - 11x + 30\), we find the roots: \[\left \{ -3, \ -2, \ - 1, \ 5 \right \}\]
  5. For \(f(x) = 2x^4 - x^3 - 9x^2 + 4x + 4 \), we find the roots: \[\left \{ -\frac{1}{2}, \ -2, \ 1, \ 2 \right \}\]
  6. We find \(f(x) = 6x^4 - 5x^3 - 14x^2 - x + 2\) has the following roots: \[\left \{ -1, \ -\frac{1}{2}, \ \frac{1}{3}, \ 2 \right \}\]
  7. We find \(f(x) = 2x^5 - 5x^4 - 24x^3 + 41x^2 + 34x - 24\) has the following roots: \[\left \{ -3, \ -1, \ \frac{1}{2}, \ 2, \ 4 \right \}\]
  8. We find the polynomial \(f(x) = 10x^5-19x^4-14x^3+23x^2+4x - 4\) has the following zeros: \[\left \{ -1, \ -\frac{1}{2}, \ \frac{2}{5}, \ 1, \ 2 \right \}\]


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe to Our Channel

Subscribe Now and view all of our playlists & tutorials.