Sum and Product of Roots of Polynomials
Here we learn the formula for the sum of the roots of a polynomial as well as the formula for the product of the roots of a polynomial.
Given a polynomial function \(f(x)\), with real or complex coefficients: \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0\] we know, thanks to the Fundamental Theorem of Algebra (FTA), that \(f(x)\) has \(n\) roots \(x_1, \ x_2, \ \dots , \ x_n\) in \(\mathbb{C}\); such that: \[f(x_1)= f(x_2)= \ \dots \ = f(x_n)=0\]
It turns out that the sum and the product of these roots are connected to the polynomial's coefficients, leading to the two formula we state below.
Sum of Roots
The sum of the roots, \(x_1 + x_2 + \dots + x_n\), will always equal to the results stated here:

Product of Roots
The product of the roots, \(x_1 \times x_2 \times \dots \times x_n\), on the other hand will always be given by:

Example 1 : Cubic Polynomial
Consider the cubic polynomial: \[f(x)=2x^3 - 8x^2 + 2x +12 \] Verify that the formula (stated above) are true.
Solution
Like all cubics, this polynomial is of degree \(3\) so \(n=3\) and the coefficients are: \[a_3 = 2, \ a_2 = -8, \ a_1 = 2, \ a_0 = 12\] so the formula for the sum and product of the roots become: \[\text{Sum of Roots} = \frac{-a_{2}}{a_3} \quad \text{and} \quad \text{Product of Roots} = \begin{pmatrix}-1\end{pmatrix}^n.\frac{a_0}{a_3}\]
Sum of the Roots
\[\begin{aligned} \text{Sum of Roots} & = \frac{-(-8)}{2} \\ & = \frac{8}{2} \\ \text{Sum of Roots} & = 4 \end{aligned}\]
Product of the Roots
\[\begin{aligned} \text{Product of Roots} & = \frac{(-1)^3\times 12}{2} \\ & = \frac{-12}{2} \\ \text{Product of Roots} & = -6 \end{aligned}\]
Checking it Works
By plotting the curve \(y = 2x^3 - 8x^2 + 2x +12\) and looking at the x-coordinates of the point(s) of intersection with the x-axis, we can quickly state that this function's roots are: \[-1, \ 2, \ \text{and} \ 3\] Consequently we have: \[\text{Sum of the Roots}=-1+2+3 = 4\] and \[\text{Product of the Roots}=-1 \times 2 \times 3 = -6\]
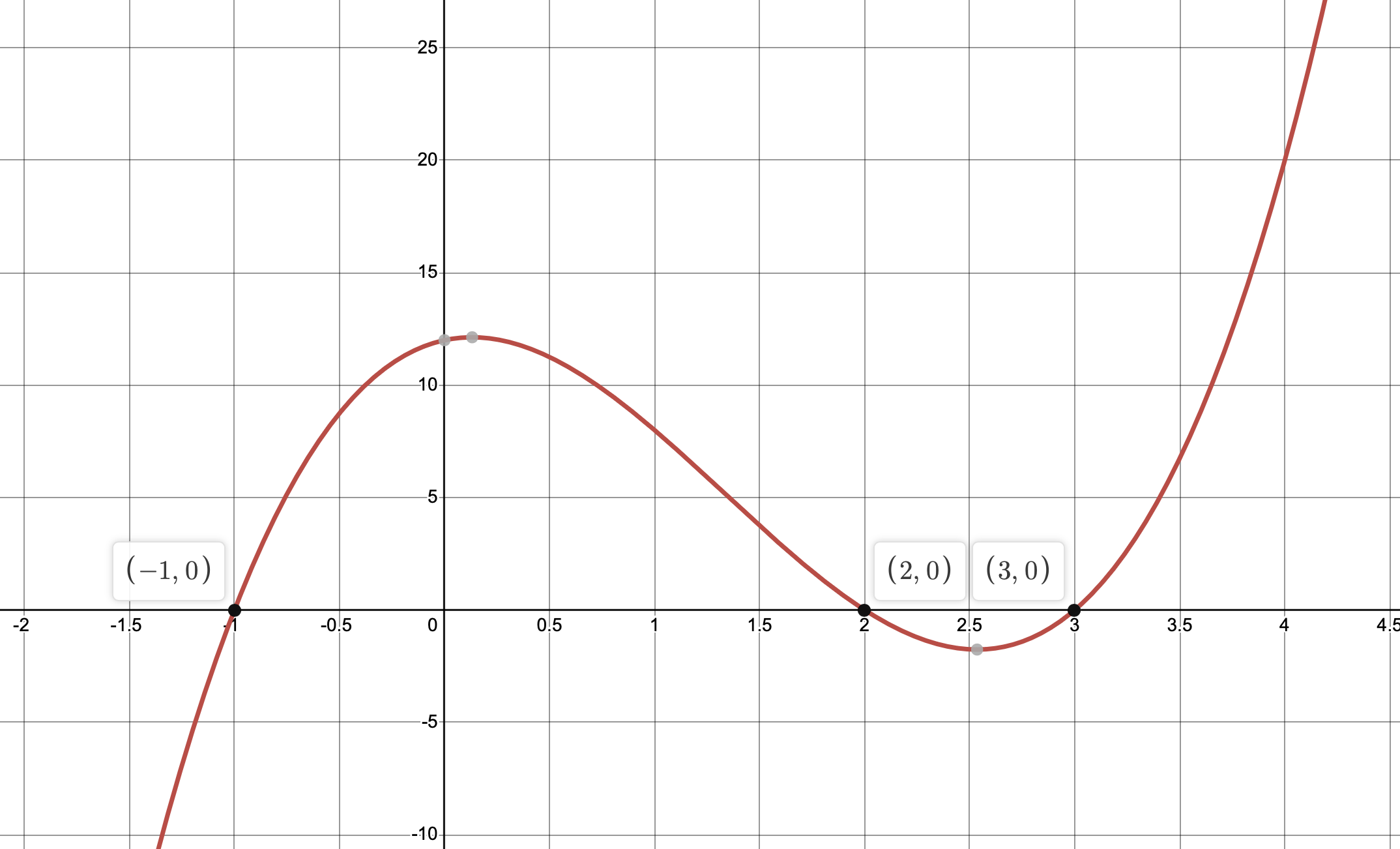
Example 2 : a "Must-Know" with Quadratics
The quadratic equation \(3x^2+5x-4=0\) has roots \(p\) and \(q\). Without solving the equation find the value of:
- \(\begin{pmatrix}p+6\end{pmatrix}\begin{pmatrix}q+6\end{pmatrix}\)
- \(p^2+q^2\)
Solution
Before we answer the questions, we notice that (since this is a quadratic) we're dealing with a polynomial of degree \(2\) and its coefficients are: \[a_2 = 3, \ a_1 = 5, \ a_0 = -4\] The formula for the sum and the product of the roots therefore lead to:
Sum of the Roots
\[\begin{aligned} \text{Sum of Roots} & = \frac{-a_1}{a_2} \\ \text{Sum of Roots} & = \frac{-5}{3} \end{aligned}\] Since the roots are \(p\) and \(q\), we can write: \[p+q = \frac{-5}{3}\]Product of the Roots
\[\begin{aligned} \text{Product of Roots} & = \frac{(-1)^2a_0}{a_2} \\ & = \frac{(-1)^2\times (-4)}{3} \\ & = \frac{1\times (-4)}{3} \\ \text{Product of Roots} & = \frac{-4}{3} \end{aligned}\] So we can write: \[pq = \frac{-4}{3}\]- The trick here is to notice that the expansion of \(\begin{pmatrix}p+6\end{pmatrix}\begin{pmatrix}q+6\end{pmatrix}\) leads to an expression that can be written in terms of the sum of the roots as well as the product of the roots \(p\) and \(q\). Indeed: \[\begin{aligned} \begin{pmatrix}p+6\end{pmatrix}\begin{pmatrix}q+6\end{pmatrix} & = pq+6p+6q+36 \\ & = pq + 6\begin{pmatrix}p+q\end{pmatrix} + 36 \end{aligned}\] and so using the fact that \(p+q = \frac{-5}{3}\) and \(pq = \frac{-4}{3}\) we obtain: \[\begin{aligned} \begin{pmatrix}p+6\end{pmatrix}\begin{pmatrix}q+6\end{pmatrix} & = pq + 6\begin{pmatrix}p+q\end{pmatrix} + 36 \\ & = \frac{-4}{3} + 6 \times \begin{pmatrix} \frac{-5}{3}\end{pmatrix} + 36 \\ & = \frac{-4}{3} -\frac{6\times 5}{3} + 36 \\ & = \frac{-4}{3} - \frac{30}{3} + \frac{108}{3} \\ & = \frac{-4-30+108}{3} \\ \begin{pmatrix}p+6\end{pmatrix}\begin{pmatrix}q+6\end{pmatrix} & = \frac{74}{3} \end{aligned}\]
-
 The key result to make a note of for this question is the fact that \(p^2+q^2\) can be written as a combination of the sum and product of \(p\) and \(q\) using:
\[p^2+q^2 = \begin{pmatrix} p+q \end{pmatrix}^2-2pq\]
Indeed using this we can write:
\[\begin{aligned}
p^2+q^2 & = \begin{pmatrix} p+q \end{pmatrix}^2-2pq \\
& = \begin{pmatrix} \frac{-5}{3} \end{pmatrix}^2 - 2\times \begin{pmatrix} \frac{-4}{3} \end{pmatrix} \\
& = \frac{(5)^2}{3^2} - 2 \times \begin{pmatrix}\frac{-4}{3} \end{pmatrix} \\
& = \frac{25}{9} - \frac{-8}{3} \\
& = \frac{25}{9} + \frac{8}{3} \\
& = \frac{25}{9} + \frac{24}{9} \\
p^2+q^2 & = \frac{49}{9}
\end{aligned}\]
The key result to make a note of for this question is the fact that \(p^2+q^2\) can be written as a combination of the sum and product of \(p\) and \(q\) using:
\[p^2+q^2 = \begin{pmatrix} p+q \end{pmatrix}^2-2pq\]
Indeed using this we can write:
\[\begin{aligned}
p^2+q^2 & = \begin{pmatrix} p+q \end{pmatrix}^2-2pq \\
& = \begin{pmatrix} \frac{-5}{3} \end{pmatrix}^2 - 2\times \begin{pmatrix} \frac{-4}{3} \end{pmatrix} \\
& = \frac{(5)^2}{3^2} - 2 \times \begin{pmatrix}\frac{-4}{3} \end{pmatrix} \\
& = \frac{25}{9} - \frac{-8}{3} \\
& = \frac{25}{9} + \frac{8}{3} \\
& = \frac{25}{9} + \frac{24}{9} \\
p^2+q^2 & = \frac{49}{9}
\end{aligned}\]
Example 3 : Polynomial with Unknown Coefficients
Given the polynomial \(p(x)=ax^4-15x^3+21x^2+9x+b\) has roots \(-1\), \(2\), \(2-i\) and \(2+i\), find \(a\) and \(b\)
Solution
Since we need to find 2 unknowns: we'll need to use 2 distinct equations. Furthermore since we're given all of this polynomial's roots we can use the sum and product of the roots formula. Given \(p(x)=ax^4-15x^3+21x^2+9x+b\) is a polynomial of ddegree \(4\), the leading coefficient is \(a_4=a\) and we can state: \[a_4 = a, \ a_3 = -15, \ a_2 = 21, \ a_1 = 9, \ a_0 = b\]
Sum of the Roots
\[\begin{aligned} \text{Sum of Roots} & = \frac{-a_3}{a_4}\\ & = \frac{-(-15)}{a} \\ \text{Sum of Roots} & = \frac{15}{a} \end{aligned}\] And, using the roots we're given in the question, we know that: \[\begin{aligned} \text{Sum of Roots} & = -1+2+\begin{pmatrix}2+i\end{pmatrix}+ \begin{pmatrix}2-i \end{pmatrix} \\ \text{Sum of Roots} & = 5 \end{aligned}\] Equating these two results we obtain: \[5 = \frac{15}{a}\] Rearranging this we can find the value of \(a\): \[\begin{aligned} 5 & = \frac{15}{a} \quad \text{(multiply both sides by \(a\))} \\ 5a & = 15 \quad \text{(divide both sides by \(5\))} \\ a & = \frac{15}{5} \\ a & =3 \end{aligned}\] So \(a=3\).Product of the Roots
\[\begin{aligned} \text{Product of Roots} & = \frac{(-1)^4 \times a_0}{a_4} \\ & = \frac{1 \times b}{a} \quad \text{(using the fact that \(a=3\)}\\ \text{Product of Roots} & = \frac{b}{3} \end{aligned}\] And, using the roots we're given in the question, we see that: \[\begin{aligned} \text{Product of Roots} &= -1\times 2 \times \begin{pmatrix}2+i\end{pmatrix} \times \begin{pmatrix}2-i \end{pmatrix} \\ \text{Product of Roots} & = -10 \end{aligned}\] Equating these two results we obtain: \[\frac{b}{3} = -10\] Using this we can quckly find \(b\): \[\begin{aligned} \frac{b}{3} & = -10 \quad \text{(multiply both sides by \(3\))}\\ b & = 3 \times (-10) \\ b & = -30 \end{aligned}\] So, \(b=-30\).Example 4 : IB AA HL Mathematics
The equation \(x^3-kx^2+3k = 0\), where \(k>0 \) has roots \(\alpha\), \(\beta\) and \(\alpha + \beta\).
Given \(\alpha \beta = -\frac{k^2}{4}\), find \(k\).
Solution
We're dealing with a cubic polynomial, so the degree is \(3\), and the coefficients are: \[a_3 = 1, \ a_2 = -k, \ a_1 = 0, \ a_0 = -3k\] It's worth pointing out that the information, given in the question, is the product of two of the three roots: \[\alpha \beta = -\frac{k^2}{4}\] This gives us the product \(\alpha \beta \) in terms of \(k\), which suggests we could find \(k\) in two steps:
- Step 1: write the third root \(\alpha + \beta \) in terms of \(k\) and solve it.
- Step 2: use the fact that the product of the roots, \(\alpha \beta \begin{pmatrix}\alpha + \beta \end{pmatrix}\) is equal to \(\frac{(-1)^3a_0}{a_3}\) to write an equation for \(k\)
For step 1 we consider the sum of the roots.
Sum of the Roots
\[\begin{aligned} \text{Sum of Roots} & = \alpha + \beta + \alpha + \beta \\ \text{Sum of Roots} & = 2\begin{pmatrix}\alpha + \beta \end{pmatrix} \quad \text{(E1)} \end{aligned}\] and we also know that: \[\begin{aligned} \text{Sum of Roots} & = \frac{-a_2}{a_3} \\ & = \frac{-(-k)}{1} \\ & = \frac{k}{1} \\ \text{Sum of Roots} & = k \quad \text{(E2)} \end{aligned}\] Equating (E1) and (E2), we obtain: \[2\begin{pmatrix}\alpha + \beta \end{pmatrix} = k\] And we can divide both sides by \(2\) to find an expression for the root \(\alpha + \beta\) in terms of \(k\): \[\begin{pmatrix}\alpha + \beta \end{pmatrix} = \frac{k}{2} \quad \text{(E3)}\]Product of the Roots
\[ \text{Product of the Roots} = \alpha \beta \begin{pmatrix} \alpha + \beta \end{pmatrix} \] Now using the fact that we are told (in the question) that \(\alpha \beta = -\frac{k^2}{4}\) and the result found in (E3), we can write the product of the roots in terms of \(k\) as: \[\begin{aligned} \text{Product of the Roots} & = \underbrace{\frac{-k^2}{4}}_{\alpha \beta} \times \underbrace{\frac{k}{2}}_{\alpha + \beta}\\ & = \frac{-k^3}{8} \quad \text{(E4)} \end{aligned}\] And the product of the roots can also be written in terms of the, given, polynomial's coefficients: \[\begin{aligned} \text{Product of Roots}& = \frac{(-1)^3a_0}{a_3} \\ & = \frac{(-1)^3 \times (3k)}{1} \\ & = \frac{-1\times (3k)}{1} \\ & = \frac{-3k}{1} \\ \text{Product of Roots} & = -3k \quad \text{(E5)} \end{aligned}\] Equating (E4) and (E5) we obtain an equation for \(k\): \[\frac{-k^3}{8} = -3k \] Now we solve: \[\begin{aligned} & \frac{-k^3}{8} = -3k \quad \text{(multiply both sides by \(-8\))} \\ & k^3 = 24k \quad \text{(subtract \(24k\) from boths sides)} \\ & k^3 - 24 k = 0 \quad \text{(write in factored form)} \\ & k\begin{pmatrix}k^2 - 24 \end{pmatrix} = 0 \end{aligned}\] For this product to equal zero, we must either have:- \(k=0\), which won't do since we're told \(k>0\) in the question, or
- \(k^2 - 24 = 0\), which leads to: \[\begin{aligned} & k^2 - 24 = 0 \\ & k^2 = 24 \\ & k = \pm \sqrt{24} \\ & k = \pm 2\sqrt{6} \end{aligned}\] This leads to two values for \(k\), \(-2\sqrt{6}\) and \(2\sqrt{6}\) but since we know that \(k>0\) only the second option will do.
Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.