Quadratic Functions & Parabola
Quadratic functions, are all of the form: \[f(x) = ax^2+bx+c\] where \(a\), \(b\) and \(c\) are known as the quadratic's coefficients and are all real numbers, with \(a\neq 0\).
Each quadratic function has a graphical representation, on the \(xy\) grid, known as a parabola whose equation is: \[y=ax^2+bx+c\]
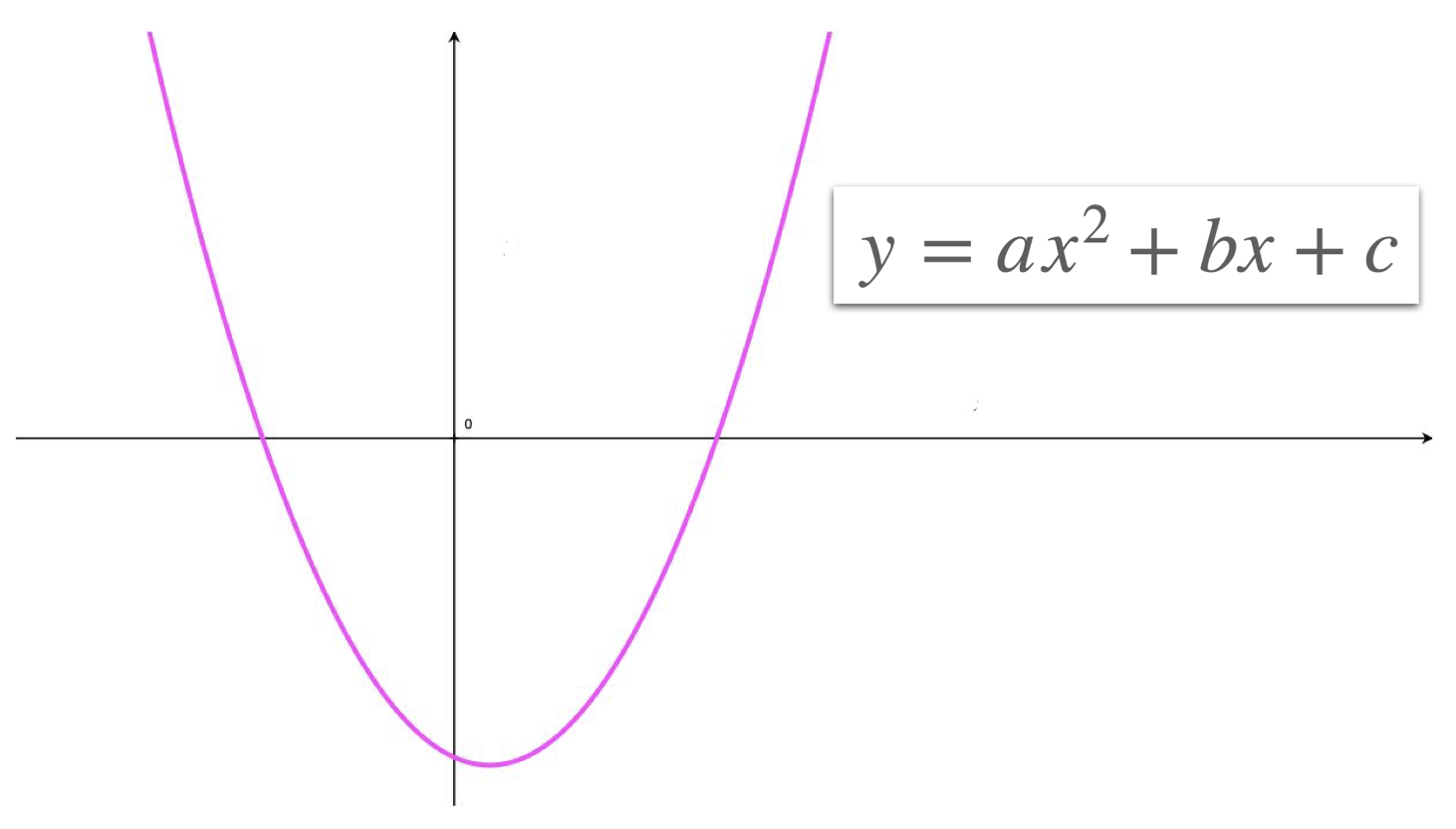
Characteristics of a Parabola
All parabola, \(y=ax^2+bx+c\)
- They are either concave-up \(\cup \) or concave-down \(\cap \).
- They all have a y-intercept; a point at which the parabola crosses the y-axis.
- They all have a vertical axis of symmetry whose equation is \(x=\frac{-b}{2a}\).
- They all have a vertex : a minimum or a maximum point.
- crosses the x-axis in 2 points
- touches the x-axis at 1 point
- doesn't cross nor touch the x-axis at all.

CONCAVE-UP or CONCAVE-DOWN
Role of \(a\)
Given a parabola \(y=ax^2+bx+c\), depending on the sign of \(a\), the \(x^2\) coefficient, it will either be concave-up or concave-down:
- \(a>0\): the parabola will be concave-up : \(\cup \)
- \(a<0\): the parabola will be concave-down : \(\cap \)

We illustrate each of these two cases here:
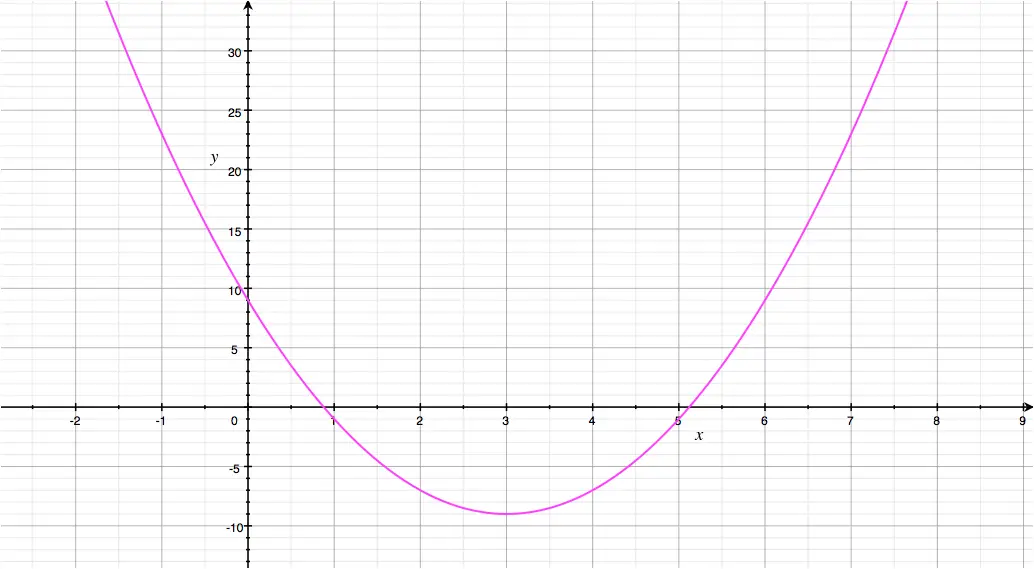
The \(x^2\) coefficient is \(2\), which is positive.
This corresponds to the \(a>0\) scenario stated above.
The parabola is shown here:
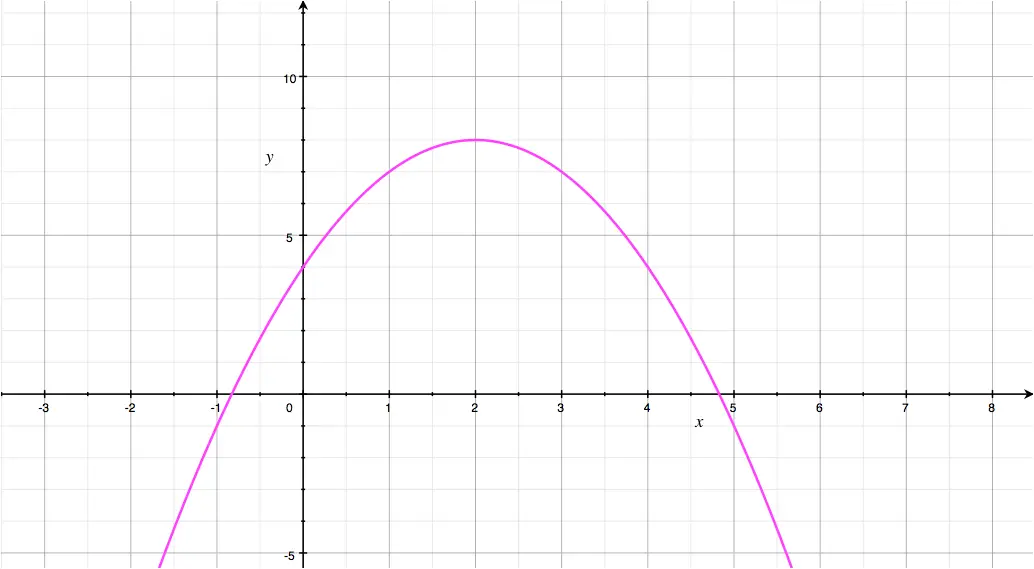
The \(x^2\) coefficient is \(-1\), which is negative.
This corresponds to the \(a< 0\) scenario stated above.
The parabola is shown here:
Y-INTERCEPT
\(y\)-intercept: Role of \(c\)
Given a parabola \(y=ax^2+bx+c\), the point at which it cuts the \(y\)-axis is known as the \(y\)-intercept.
The \(y\)-intercept will always have coordinates: \[\begin{pmatrix}0,c\end{pmatrix}\] where \(c\) is the only term in the parabola's equation without an \(x\).

Example
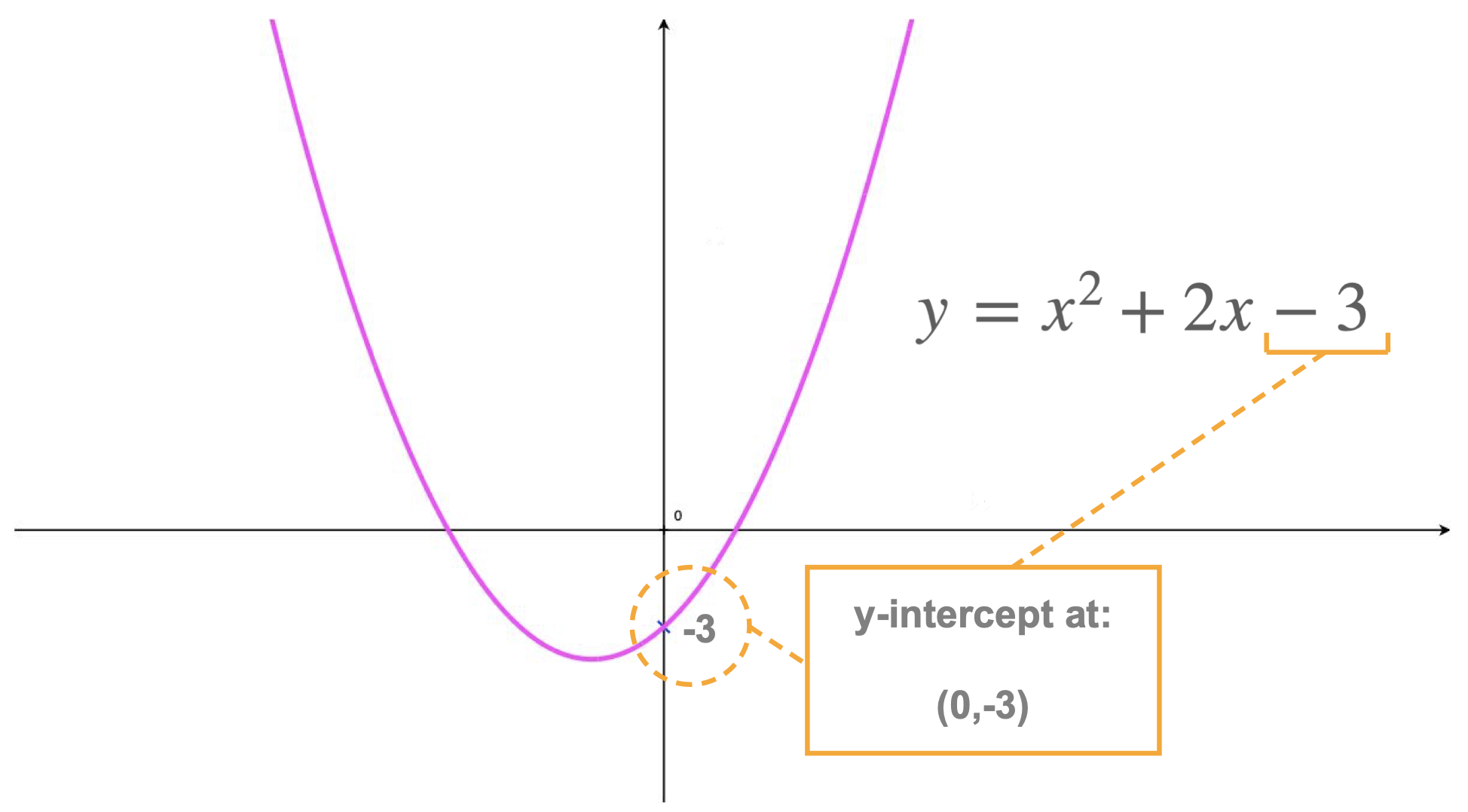
Given the parabola defined by: \[y = x^2+2x-3\] State its y-intercept.
Solution
At the y-intercept \(x=0\) so replacing \(x\) by \(0\) in the parabola's equation: \[\begin{aligned} y & = 0^2 + 2\times 0 - 3\\ & = 0 + 0 - 3 \\ y &= -3 \end{aligned}\] So the y-intercept is the point with coordinates \(\begin{pmatrix}0,-3\end{pmatrix}\).
Note: you don't need to show the working when you replace \(x\) by \(0\) and can state the answer directly.
The y-intercept can be seen on this parabola's graph:
Axis of Symmetry
All parabola have a vertical axis of symmetry, that is a vertical line across of which the parabola is the mirror image of itself.
Given a parabola \(y=ax^2 + bx + c\), the equation of its axis of symmetry can always be found using the formula: \[x = \frac{-b}{2a}\]

Tutorial : How To Find The Axis of Symmetry
In this video we learn how to use the formula \(x = \frac{-b}{2a}\) to find a parabola's axis of symmetry.
Example
Given the parabola defined by: \[y = x^2 - 6x+5\] State the equation of its axis of symmetry.
Solution
Comparing \(y=x^2-6x+5\) to the generic \(y=ax^2+bx+c\), we see that \(a = 1\), \(b=-6\) and \(c=5\). Using these values and the formula for the axis of symmetry we find: \[\begin{aligned} x & = \frac{-b}{2a} \\ & = \frac{-(-6)}{2\times 1} \\ & = \frac{6}{2} \\ x & = 3 \end{aligned}\] This parabola's vertical axis of symmetry has equation: \[x = 3\] This is illustrated in the graph we see here, where the axis of symmetry is the dotted line.

VERTEX OF A PARABOLA
Given a quadratic function \(f(x) = ax^2+bx+c\), depending on the sign of the \(x^2\) coefficient, \(a\), its parabola has either a minimum or a maximum point:
- if \(a>0\): it has a minimum point
- if \(a<0\): it has a maximum point
Finding the Vertex
To find the vertex we calculate its \(x\)-coordinate, \(h\), with the formula given below.
We then calculate its \(y\)-coordinate, \(k\), by plugging in the
- Step 1: calculate the \(x\)-coordinate of the vertex, \(h\), using the formula: \[h = \frac{-b}{2a}\]
- Step 2: calculate the \(y\)-coordinate of the vertex, \(k\), by replacing \(x\) inside \(y=ax^2+bx+c\) by the value we found for \(h\), in step 1.
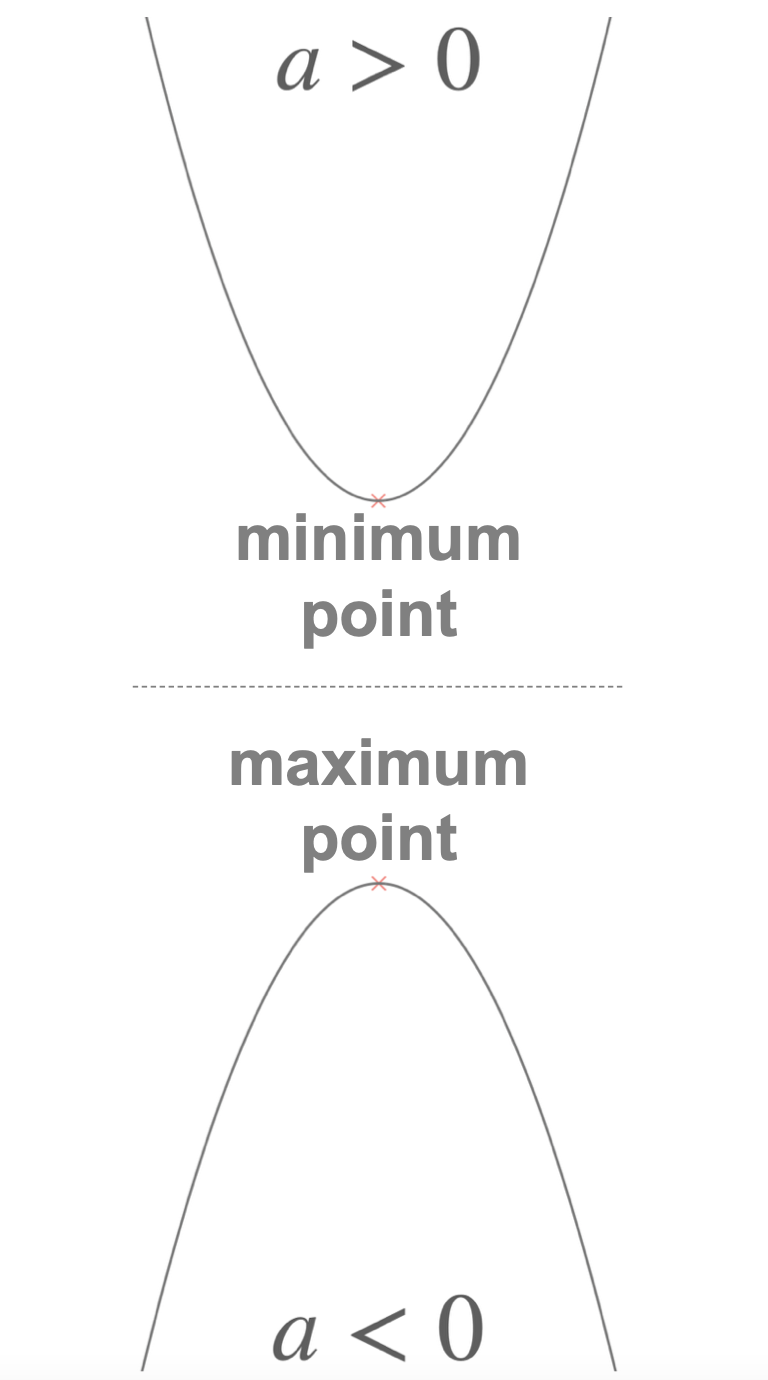
Remember: the vertex is the parabola's maximum or minimum point. We often refer to its coordinates with the letters \(h\) and \(k\) and say that it has coordinates: \(\begin{pmatrix}h,k\end{pmatrix}\).
The 2-step method for finding the coordinates of a parabola's vertex are best explained in the tutorial below.
Tutorial : Coordinates of the Vertex
In the following tutorial we learn how to find the coordinates of a parabola's vertex, in other words the coordinates of its maximum, or minimum, point.
Example
Consider quadratic function whose parabola is described by: \[y = 2x^2 - 4x - 6\]
- State whether this parabola's vertex is a maximum, or a minimum.
- Find the coordinates of this parabola's vertex.
Solution
- The \(x^2\) coefficient is \(2\). Since \(2>0\) this parabola's vertex is a minimum point.
-
To find the coordinates of the vertex, we follow the two steps we read further-up:
- Step 1: we calculate the \(x\)-coordinate, \(h\), of the vertex using the formula: \[h = \frac{-b}{2a}\] Looking at \(y=2x^2 - 4x-6\), we see that: \[a = 2, \ b = -4, \ c = -6\] So the formula for the \(x\)-coordinate becomes: \[\begin{aligned} h & = \frac{-b}{2a}\\ & = \frac{-(-4)}{2\times 2} \\ & = \frac{4}{4} \\ h & = 1 \end{aligned}\] So the \(x\)-coordinate of the vertex is \(h=1\).
-
Step 2: we calculate the \(y\)-coordinate of the vertex by replacing \(x\) by \(1\) inside \(y=2x^2-4x-6\) and calculating the value of \(y\).
That's: \[\begin{aligned} y & = 2\times 1^2-4\times 1-6 \\ & = 2\times 1 - 4 - 6 \\ & = 2 - 4 - 6 \\ & = -2 - 6 \\ y & = -8 \end{aligned}\] So the \(y\)-coordinate of the vertex is \(k=-8\).

X-INTERCEPTS & The DISCRIMINANT \(\Delta \)
X-Intercepts and Role of the Discriminant \(\Delta\)
Given a quadratic function \(f(x) = ax^2+bx+c\) and its parabola \(y=ax^2+bx+c\), its x-intercepts are the points at which the curve crosses the x-axis.
The values of x at which it cuts the x-axis are the solution(s) to the equation: \[0=ax^2+bx+c\] and the discriminant, written \(\Delta\), tells us how many solutions that equation has and, consequently, the number of times the curve cuts, or crosses, the x axis.
The discriminant is calculated with the formula: \[\Delta = b^2 - 4ac\] Then, depending on the sign (positive, zero, or negative) of \(\Delta\) the curve will cuts the x-axis 2 times, 1 time, or not at all.
Remember: the values of x at which the parabola cuts the x-axis are found by solving the equation \(0=ax^2+bx+c\).
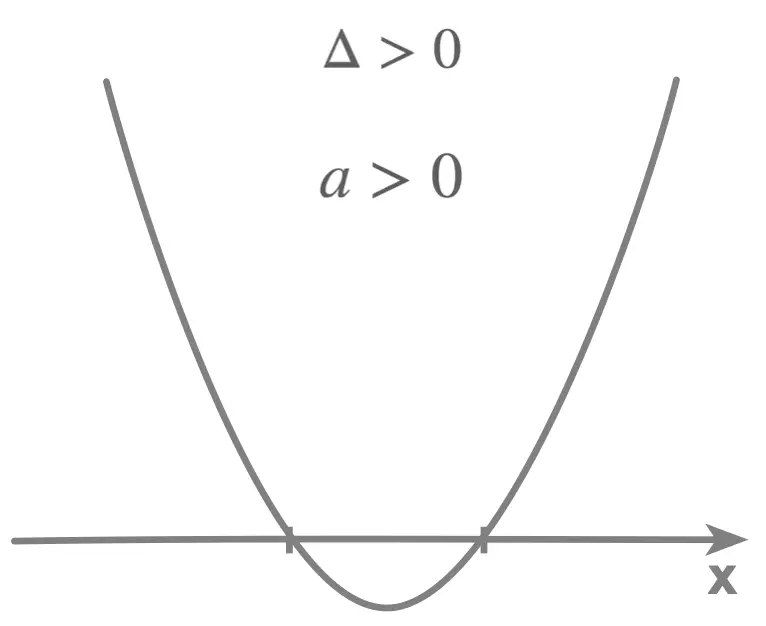
Posistive Discriminant : \(\Delta > 0\)

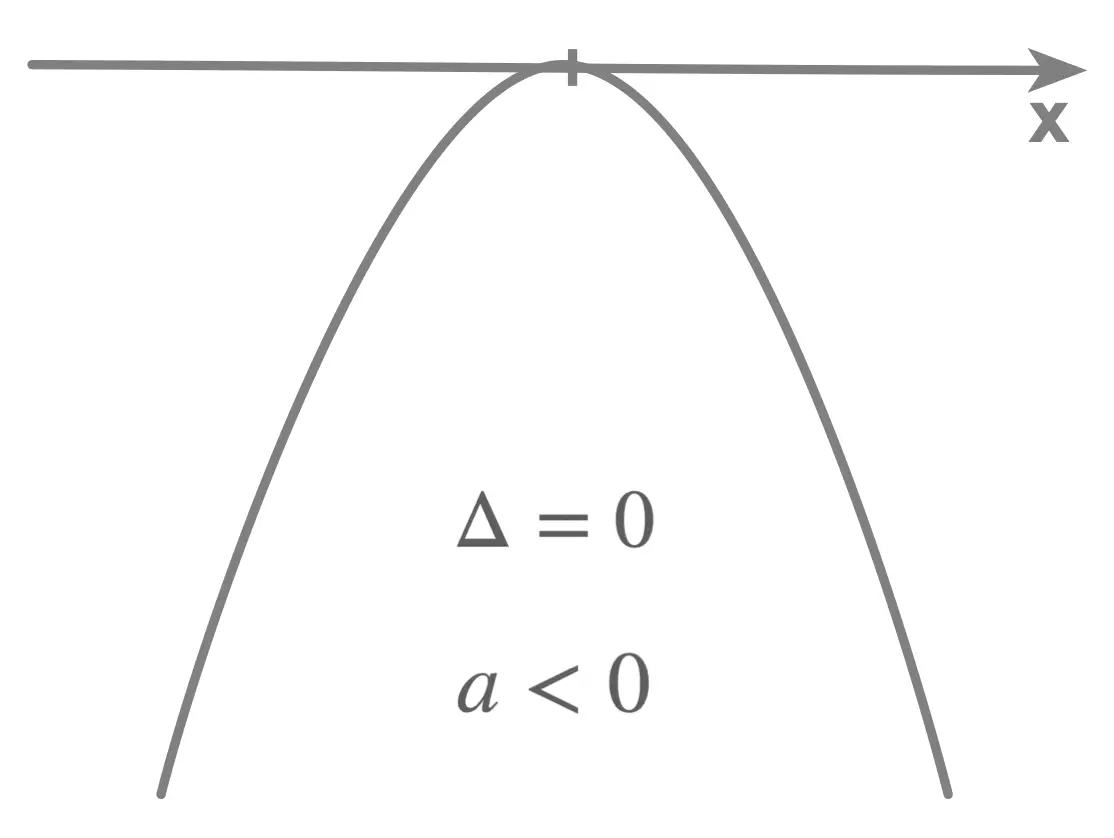
Zero Discriminant : \(\Delta = 0\)

Negative Discriminant : \(\Delta < 0\)


3 Cases
- \(\Delta > 0\): the parabola cuts the x axis in 2 points, we say the parabola has 2 x intercepts, or 2 zeros, given by: \[x = \frac{-b \pm \sqrt{\Delta}}{2a}\]
- \(\Delta = 0\): the parabola touches the x axis in 1 point, we say the parabola has 1 x intercept, or 1 zero, given by: \[x = \frac{-b}{2a}\]
- \(\Delta < 0\): the parabola doesn't cross or touch the x axis at all; it is either completely above the x axis, or completely below it.
Example 1 : \(\Delta >0\)
Find the \(x\)-intercept(s) for the parabola: \[y=3x^2 - 3x - 6\]
Solution
The parabola \(y = 3x^2 - 3x-6\) cuts the \(x\)-axis when \[3x^2-3x-6 = 0\] We solve this equation in two steps
- Step 1: calculate the discriminant \(\Delta \): \[\begin{aligned} \Delta & = b^2 - 4ac\\ & = (-3)^2-4\times 3\times (-6)\\ & = 9 - 12 \times (-6) \\ & = 9 - (-72)\\ & = 9 + 72 \\ \Delta & = 81 \end{aligned}\]
-
Step 2: we now solve the equation, according to the sign of \(\Delta\).
Since \(\Delta >0\) the equation has two solutions, given by the formula: \[x = \frac{-b\pm \sqrt{\Delta}}{2a}\] replacing \(\Delta\), \(a\) and \(b\) by their respective values leads to: \[\begin{aligned}x &= \frac{-b\pm \sqrt{\Delta}}{2a} \\ & = \frac{-(-3) \pm \sqrt{81}}{2\times 3} \\ & = \frac{3 \pm 9}{6} \\ x & = \frac{1 \pm 3}{2} \\ \end{aligned}\] So the equation \(3x^2 - 3x-6 = 0\) has two solutions:\[\begin{aligned} x & = \frac{1 - 3}{2} \\ & = \frac{-2}{2} \\ x & = -1 \end{aligned}\]\[\begin{aligned} x & = \frac{1 + 3}{2} \\ & = \frac{4}{2} \\ x & = 2 \end{aligned}\]
This means that the parabola cuts the \(x\)-axis twice, at:
\[x = \begin{pmatrix}-1,0\end{pmatrix} \quad \text{and} \quad x = \begin{pmatrix}2,0\end{pmatrix} \]
These two points are known as the parabola's \(x\)-intercepts.
Looking at the parabola \(y = 3x^2 - 3x-6\) on an \(xy\)-grid we can confirm these results:

Example 2 : \(\Delta = 0\)
Find the x-intercepts for the parabola: \[y=-x^2 - 8x - 16\]
The parabola \(y = -x^2-8x-16\) cuts the \(x\)-axis when: \[-x^2-8x-16 = 0\] We solve this equation in two-steps:
- Step 1: calculate the discriminant \(\Delta \): \[\begin{aligned} \Delta & = b^2 - 4ac\\ & = (-8)^2-4\times (-1)\times (-16\) \\ & = 64 - (-4)\times (-16)\\ & = 64 - 64 \\ \Delta & = 0 \end{aligned}\]
-
Step 2: we now solve the equation, according to the sign of \(\Delta\).
Since \(\Delta = 0\) the equation has one solution, given by the formula: \[x = \frac{-b}{2a}\] replacing \(a\) and \(b\) by their respective values leads to: \[\begin{aligned} x & = \frac{-b}{2a} \\ & = \frac{-(-8)}{2\times (-1)} \\ & = \frac{8}{-2} \\ x & = -4 \end{aligned}\] The solution to this equation is \(x = -4\).
Looking at the parabola \(y = -x^2-8x-16\) on an \(xy\)-grid we can confirm this result:

Example 3 : \(\Delta < 0\)
Find the x-intercepts for the parabola: \[y = 2x^2-4x+5\]
The parabola \(y = 2x^2-4x+5\) cuts the \(x\)-axis when: \[2x^2-4x+5 = 0\] We solve this equation in two-steps:
- Step 1: calculate the discriminant \(\Delta \): \[\begin{aligned} \Delta & = b^2 - 4ac\\ & = (-4)^2 - 4\times 2\times 5 \\ & = 16 - 8 \times 5 \\ & = 16 - 40 \\ \Delta & = -24 \end{aligned}\]
-
Step 2: we now solve the equation, according to the sign of \(\Delta\).
Since \(\Delta < 0\) the equation has no real solution

Scan this QR-Code with your phone/tablet and view this page on your preferred device.
Subscribe Now and view all of our playlists & tutorials.