Linear Sequences
Difference Method
Linear sequences of numbers are characterized by the fact that to get from one term to the next we always add the same amount.
The amount we add is known as the difference, frequently called the common difference.
For example, the sequences:
\[3,7,11,15,19,23, \dots \]
For the first, we always add \(3\) and for the second we always add \(-2\).
Here we illustrate this further for the first linear sequence:
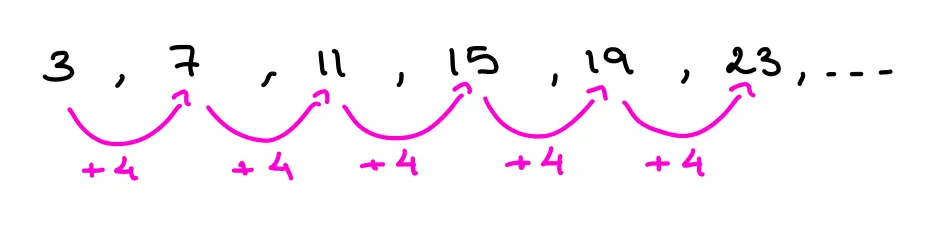
We can see quite clearly that we're always adding the same amount to get from one term to the next, this means it is a linear sequence.
Formula for the \(n^{\text{th}}\) term
If a sequence is linear then its formula can be written:
\[u_n = an+b\]
For example, the sequence whose first few terms are:
\[3,7,11,15,19,23, \dots \]
has formula:
\[u_n = 4n - 1\]
This lets us calculate any term of the sequence directly.
For instance to calculate the \(4^{\text{th}}\) term we would replace \(n\) by \(4\) in our formula:
\[\begin{aligned} u_4 &= 4\times 4 - 1 \\
& = 16 - 1 \\
u_4 &= 15
\end{aligned}\]
We learn how to find the formula for the \(n^{\text{th}}\) term below.
Method - Finding the formula for the \(n^{\text{th}}\) term
Given the first few terms of a linear sequence, we find its formula
\[u_n = an+b\]
using the following two equations:
\[\begin{cases}
a = \text{difference between first two terms} \\
a+b = \text{first term of the sequence}
\end{cases}\]
To illustrate this further, we look at our sequence \(3,7,11,15,19,23, \dots\).
For this sequence these equations tell us:
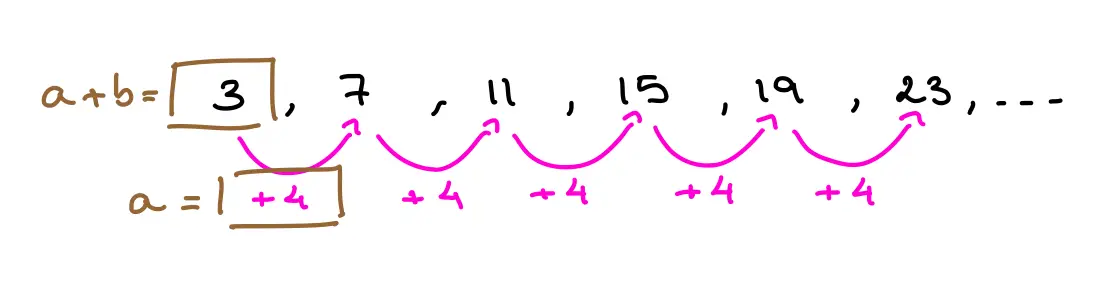
Looking at this, and the two equations we saw above, each of the equations is:
\[\begin{cases}
a = 4 \\
a+b = 3
\end{cases}\]
Using these two equations, we can find each of the coefficients \(a\) and \(b\).
The method for using this formula is illustrated in the tutorial below.
Tutorial
In the following tutorial we review the method for findng the formula for the \(n^{\text{th}}\) term of a linear sequence. Watch it now.
Exercise
Find the formula for the \(n^{\text{th}}\) term of each of the following sequences:
- The sequence whose first few terms are: \[2,6,10,14,18, \dots \]
- The sequence whose first few terms are: \[13,10,7,4,1, \dots \]
- The sequence whose first few terms are: \[-3,4,11,18,25, \dots \]
- The sequence whose first few terms are: \[3,3.5,4,4.5,5, \dots \]
- The sequence whose first few terms are: \[12, 5, -2, -9, -16, \dots \]
Answers Without Working
- \(u_n = 4n-2\)
- \(u_n = -3n + 16\)
- \(u_n = 7n - 10\)
- \(u_n = 0.5n +2.5\)
- \(u_n = -7n + 19\)