RadfordMathematics.com

Quadratic Sequences - Difference Method

Formula for the n-th term

Quadratic sequences of numbers are characterized by the fact that the difference between terms always changes by the same amount.

Consequently, the "difference between the differences between the sequence's terms is always the same". We say that the second difference is constant.

Here's what we mean, consider the sequence: \[6,11,18,27,38,51 \dots \] looking at the first and "second differences" of this sequence would look like:

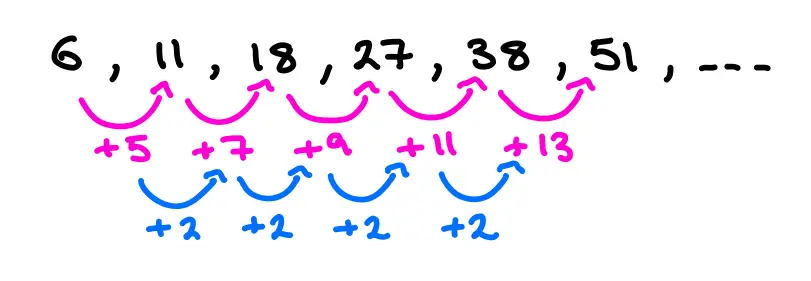
Looking at this we can see that the second difference is constant, and not equal to zero, this means it is a quadratic sequence.

Formula for the \(n^{\text{th}}\) term

If a sequence is quadratic then its formula can be written: \[u_n = an^2+bn+c\] For example, the sequence, we saw above: \(6,11,18,27,38,51 \dots \) has formula: \[u_n = n^2 + 2n + 3 \] Indeed, if we replace \(n\) by (for example) \(1\) and \(2\) we'll find the first and second terms of the sequence, that's: \[\begin{aligned} u_1 & = 1^2 + 2\times 1 + 3 \\ &= 1 + 2 +3 \\ u_1 & = 6 \end{aligned} \]

and
\[\begin{aligned} u_2 &= 2^2 + 2\times 2 + 3 \\ & = 4 + 4 + 3 \\ u_2 & = 11 \end{aligned} \] We learn how to find the formula for the \(n^{\text{th}}\) term below.

Method - Finding the formula for a Quadratic Sequence

Given the first few terms of a quadratic sequence, we find its formula \[u_n = an^2 + bn +c\] by finding the values of the coefficients \(a\), \(b\) and \(c\) using the following three equations: \[\begin{cases} 2a = 2^{\text{nd}} \ \text{difference}\\ 3a + b = u_2 - u_1 \\ a+b+c = u_1 \end{cases}\] Where:

  • \(u_2-u_1\): is the difference between the first two terms of the sequence.
  • \(u_1\): is the first term of the sequence.

Example

The following illustration shows all of the differences we're referring to in these equations, for the quadratic sequence: \(6,11,18,27,38,51 \dots \)


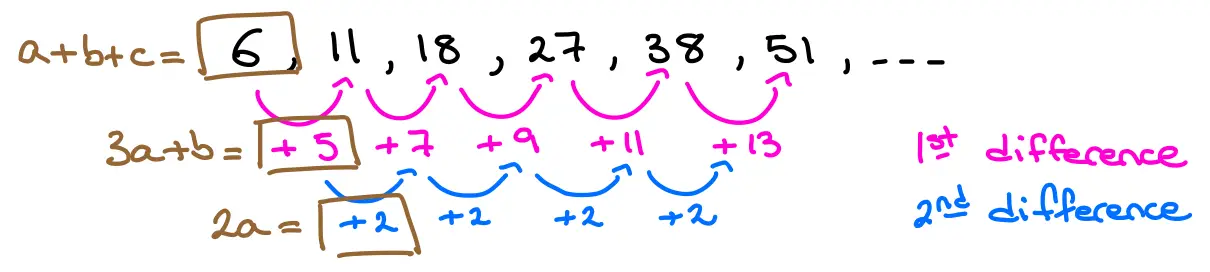
Looking at this, and the formula we saw above, each of the equations is: \[\begin{cases} 2a = 2\\ 3a + b = 5\\ a+b+c = 6 \end{cases}\] We can see that the values that we use, the ones we've boxed in the illustration, are always the first on each row.

Using each of these equations, in the order they're stated here, we can find each of the three coefficients \(a\), \(b\) and \(c\).

This is best explained in the following tutorial, watch it now.

Tutorial: Formula for the \(n^{\text{th}}\) term

In the following tutorial we learn the method for finding the formula for the n-th term of a quadratic sequence.

Exercise

Find the formula for the \(n^{\text{th}}\) term of each of the following sequences:

  1. The sequence whose first few terms are: \[-3,0,5,12,21,32, \dots \]
  2. The sequence whose first few terms are: \[-4,2,12,26,44,66,92, \dots \]
  3. The sequence whose first few terms are: \[2,6,12,20,30,42,56, \dots \]
  4. The sequence whose first few terms are: \[1,0,-3,-8,-15,-24,-35, \dots \]
  5. The sequence whose first few terms are: \[3,7,13,21,31,43,57, \dots \]

Note: this exercise can be downloaded as a worksheet to practice with: worksheet

Answers Without Working

  1. \(u_n = n^2 - 4\)
  2. \(u_n = 2n^2 - 6\)
  3. \(u_n = n^2 + n\)
  4. \(u_n = -n^2+2n\)
  5. \(u_n = n^2 + n + 1\)


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.