Arithmetic Sequences - Formula for the n-th Term

(Linear Sequences)

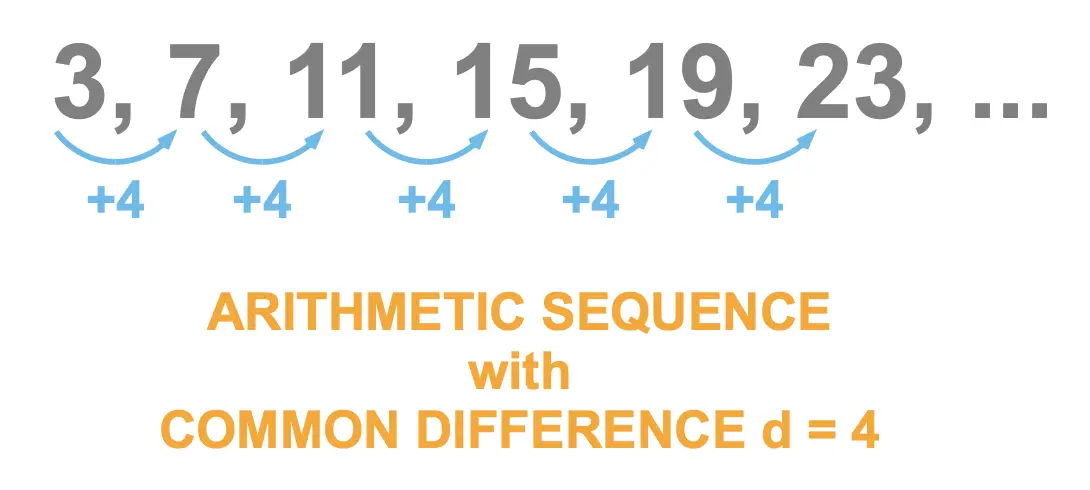In an arithmetic sequence, also known as linear sequence, we always add the same amount to get from one term to the next. The amount we add is known as the common difference and we use the letter \(d\) to refer to it.

Here are some examples of arithmetic sequences:

\(2, \ 7, \ 12, \ 17, \ 22, \ \dots \) an arithmetic sequence with common difference \(d = 5\)
\(8, \ 5, \ 2, \ -1, \ -4, \ \dots \) an arithmetic sequence with common difference \(d = -3\)
\(32, \ 30.5, \ 29, \ 27.5, \ 26, \ \dots \) an arithmetic sequence with common difference \(d = -1.5\)

Introduction to Arithmetic Sequences & Formula for n-th term

In this tutorial we introduce arithmetic sequences and learn the formula for the n-th term.

FORMULA (for the n-th term)

Given an arithmetic sequence we can calculate any of its terms using the formula: \[u_n = u_1 + \begin{pmatrix}n - 1\end{pmatrix}.d\] where:

\(u_1\): is the first term of the sequence
\(d\): is the common difference

EXAMPLE

Given the following sequence of numbers: \[3, \ 7, \ 11, \ 15, \ 19, \ \dots \]

Find its formula for the n-th term (formula for calculating any term).
Calculate the 10th term.

Solution

This is an arithmetic sequence whose common difference is \(d = 4\); indeed to get from any one term to the next we always add \(4\).

To define this arithmetic sequence's n-th term all we need is:

the first term, which is \(u_1 = 3\)
the common difference, which is \(d = 4\)

replacing both \(u_1\) and \(d\) in the formula \(u_n = u_1 + \begin{pmatrix}n - 1\end{pmatrix}.d\) leads to: \[u_n = 3 + \begin{pmatrix}n-1\end{pmatrix}.4\] Using this formula we can calculate any term of the sequence, all we have to do is replace every \(n\) we see inside the formula by the number of the term we wish to find.

For example, if we want to calculate the 10-th term then we would replace every \(n\) we see by \(10\), as shown here: \[\begin{aligned} u_{10} & = 3 + \begin{pmatrix} 10 - 1 \end{pmatrix}.4 \\ & = 3 + 9\times 4 \\ & = 3 + 36 \\ u_{10} & = 39 \end{aligned}\]

Arithmetic or Linear Sequences

The formula for the n-th term of an arithmetic sequence can also be written: \[u_n = dn+c\] where \(c\) is a constant.(in fact \(c = u_1 - d\)).

Starting from \(u_n = u_1 + \begin{pmatrix}n-1\end{pmatrix}.d\) and expanding the parentheses we can quickly see that \(c = u_1-d\). Indeed: \[\begin{aligned} u_n & = u_1 + \begin{pmatrix}n-1\end{pmatrix}.d \\ & = u_1 + dn - d \\ u_n & = dn + \underbrace{u_1 - d}_{c} \end{aligned}\]

Example

The arithmetic sequence whose formula was: \[u_n = 3 + \begin{pmatrix} n - 1 \end{pmatrix}.4\] can also be written: \[u_n = 4n - 1\]

Tutorial

In this tutorial we see how any arithmetic sequence can be written as a linear sequence.

Common Difference Formula

Given an arithmetic sequence, we can always find the common difference using: \[d = u_{n+1}-u_n\] which we can also write: \[d = u_n-u_{n-1}\]

Explanation

This formula tells us that, guven an arithmetic sequence, we can find the common difference \(d\) by subtracting any term from the next.

For example, given the arithmetic sequence: \[3,7,11,15,19,23, \dots \] we can calculate \(d\) using either of the following:

Using the first and second terms: \[ \begin{aligned} d & = u_2-u_1 \\ & = 7-3 \\ d &=4 \end{aligned}\]
Using the second and third terms: \[\begin{aligned} d & = u_3-u_2 \\ & = 11-7\\ d & =4 \end{aligned}\]
Using the third and fourth terms: \[\begin{aligned} d &= u_4-u_3 \\ & = 15-11 \\ d &=4 \end{aligned}\]

\(\vdots \)

Exercise 1

For each of the arithmetic sequences, from a to e, do each of the following:

State the value of \(u_1\).
State the value of the common difference \(d\).
Find the formula for the n-th term, written in both formats:
1. \(u_n = u_1 + \begin{pmatrix}n-1\end{pmatrix}.d\)
2. \(u_n = d.n+c\)
Calculate the term indicated in brackets.
1. \(-2, \ 1, \ 4, \ 7, \ 10, \ \dots \ \begin{bmatrix} u_7 \end{bmatrix}\)
2. \(41, \ 39, \ 37, \ 35, \ 33, \ \dots \ \begin{bmatrix} u_{21} \end{bmatrix}\)
3. \(7, \ 7.5, \ 8, \ 8.5, \ 9, \ \dots \ \begin{bmatrix} u_{53} \end{bmatrix}\)
4. \(9, \ 16, \ 23, \ 30, \ 37, \ \dots \ \begin{bmatrix} u_{100} \end{bmatrix} \)
5. \(32, \ 27, \ 22, \ 17, \ 12, \dots \ \begin{bmatrix} u_{65} \end{bmatrix}\)

1. \(u_1 = -2\)
2. \(d = 3\)
3. we find:
  1. \(u_n = -2 + \begin{pmatrix}n - 1 \end{pmatrix} \times 3\)
  2. \(u_n = 3n-5\)
4. we find \(u_7\) as follows: \[\begin{aligned} u_7 & = -2 + \begin{pmatrix}7 - 1 \end{pmatrix} \times 3 \\ & = -2 + 6 \times 3 \\ & = -2 + 18 \\ u_7 & = 16 \end{aligned}\]

1. \(u_1 = 41\)
2. \(d = -2\)
3. we find:
  1. \(u_n = 41 + \begin{pmatrix} n - 1 \end{pmatrix} \times (-2)\)
  2. \(u_n = -2n-39\)
4. we find \(u_{21}\) as follows: \[\begin{aligned} u_{21} & = 41 + \begin{pmatrix} 21 - 1 \end{pmatrix} \times (-2) \\ & = 41 + 20 \times (-2)\\ & = 41 + (-40) \\ u_{21} & = 1 \end{aligned}\]

we find:
1. \(u_1 = 7\)
2. \(d = 0.5 = \frac{1}{2}\)
3. we find:
  1. \(u_n = 7 + \begin{pmatrix}n-1\end{pmatrix} \times \frac{1}{2}\)
  2. \(u_n = \frac{n}{2} +6.5\)
4. we find \(u_{53}\) as follows: \[\begin{aligned} u_{53} & = 7 + \begin{pmatrix} 53 - 1 \end{pmatrix} \times \frac{1}{2} \\ & = 7 + 52 \times \frac{1}{2} \\ & = 7 + 26 \\ u_{53} & = 33 \end{aligned}\]

1. \(u_1 = 9\)
2. \(d = 7\)
3. we find:
  1. \(u_n = 9 + \begin{pmatrix} n - 1 \end{pmatrix} \times 7 \)
  2. \(u_n = 7n+2\)
4. we find \(u_{100}\) as follows: \[\begin{aligned} u_{100} & = 9 + \begin{pmatrix} 100 - 1 \end{pmatrix} \times 7 \\ & = 9 + 99 \times 7 \\ & = 9 + 693 \\ u_{100} & = 702 \end{aligned}\]

1. \(u_1 = 32\)
2. \(d = -5\)
3. we find:
  1. \(u_n = 32 + \begin{pmatrix}n-1 \end{pmatrix} \times (-5) \)
  2. \(u_n = -5n+37\)
4. we find \(u_{65}\) as follows: \[\begin{aligned} u_{65} & = 32 + \begin{pmatrix} 65 -1 \end{pmatrix} \times (-5) \\ & = 32 + 64 \times (-5) \\ & = 32 + (-320) \\ u_{65}& = -288 \end{aligned}\]

EXAM STYLE Questions

We now learn how to solve some typical exam style questions involving arithmetic sequences and the formula for the n-th term.

Start by watching the following tutorials.

Exam Question 1

An arithmetic sequence has first term equal to \(5\) and eigth term equal to \(54\).

Find this sequence's common difference \(d\).

The detailed solution to this question is shown in the tutorial shown here.

Exam Question 1

Exam Question 2

An arithmetic sequence has third term equal to \(4\) and seventh term equal to \(22\).

Find this sequence's first term \(u_1\) and common difference \(d\).

The detailed solution to this question is shown in the tutorial shown here.

Exam Question 2

Exercise 2

An arithmetic sequence has first term equal to \(-5\) and fifth term equal to \(7\). Find this sequence's common difference.

An arithmetic sequence has fifth term equal to \(1\) and ninth term equal to \(-7\). Find this sequence's first term and common difference.

An arithmetic progression has tenth term equal to \(8\) and second term equal to \(4\). Find its first term and its common difference.

An arithmetic sequence has first term \(u_1 = 11\) and seventh term \(u_7 = -13\). Find this sequence's common difference \(d\).

Given an arithmetic sequence has 5th term equal to \(10\) and 20th term equal to \(13\), find this sequence's first term and common difference.

Given an arithmetic progression whose first term is \(u_1 = -1\) and fifth term is \(-29\), find this sequence's common difference.

An arithmetic sequence has 6th term equal to \(19\) and 3rd term equal to \(1\). Find this seqence's first term and its common differendce.

An arithmetic sequence has 10th term equal to \(53\) and 4th term equal to \(17\). Find its first term and its common difference.

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

We find:
- common difference: \(d = 3\)
- formula for n-th term: \(u_n = -5 + \begin{pmatrix}n-1\end{pmatrix}.3\), which can also be written \(u_n = 3n-8\).

We find:
- common difference: \(d = -2\)
- first term: \(u_1 = 9\)
- formula for n-th term: \(u_n = 9 + \begin{pmatrix}n-1\end{pmatrix}.(-2)\), which can also be written \(u_n = -2n+11\).

We find:
- common difference: \(d = 0.5\)
- first term: \(u_1 = 3.5\)
- formula for n-th term: \(u_n = 3.5 + \begin{pmatrix}n-1\end{pmatrix}\times 0.5\), which can also be written \(u_n = 0.5n+3\).

We find:
- common difference: \(d = -4\)
- formula for n-th term: \(u_n = 11 + \begin{pmatrix}n-1\end{pmatrix}.(-4)\), which can also be written \(u_n = -4n+15\).

We find:
- common difference: \(d = 0.2\)
- first term: \(u_1 = 9.2\)
- formula for n-th term: \(u_n = 9.2 + \begin{pmatrix}n-1\end{pmatrix}\times 0.2\), which can also be written \(u_n = 0.2n+9\).

We find:
- common difference: \(d = -7\)
- formula for n-th term: \(u_n = -1 + \begin{pmatrix}n-1\end{pmatrix}.(-7)\), which can also be written \(u_n = -7n+6\).

We find:
- common difference: \(d = 3\)
- first term: \(u_1 = -5\)
- formula for n-th term: \(u_n = -5 + \begin{pmatrix}n-1\end{pmatrix}.3\), which can also be written \(u_n = 3n-8\).

We find:
- common difference: \(d = 6\)
- first term: \(u_1 = -1\)
- formula for n-th term: \(u_n = -1 + \begin{pmatrix}n-1\end{pmatrix}.6\), which can also be written \(u_n = 6n-7\).

Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.

RadfordMathematics.com

Online Mathematics Book

Arithmetic Sequences - Formula for the n-th Term

(Linear Sequences)

Introduction to Arithmetic Sequences & Formula for n-th term

FORMULA (for the n-th term)