RadfordMathematics.com

Geometric Sequences & Series

GEOMETRIC SEQUENCES

Formula for the n-th term

In an geometric sequence we always multiply by the same amount to get from one term to the next. The amount we multiply by is known as the common ratio and we use the letter \(r\) to refer to it.

Here are some examples of geometric sequences:

  • \(3, \ 6, \ 12, \ 24, \ 48, \ \dots \) a geometric sequence with common ratio \(r = 2\)
  • \(243, \ 81, \ 27, \ 9, \ 3, \ \dots \) a geometric sequence with common ratio \(r = \frac{1}{3}\)
  • \(2, \ -10, \ 50, \ -250, \ 1250, \ \dots \) a geometric sequence with common ratio \(r = -5\)

Tutorial: Geometric Sequences

In the following tutorial we learn the formula for calculating the sum of the first n terms of a geometric sequence and learn how to use it with a worked example.

Geometric Sequences : Formula for the n-th term

Given a geometric sequence with first term \(u_1\) and common ratio \(r\), we can calculate any term of the sequence directly using the formula shown here:

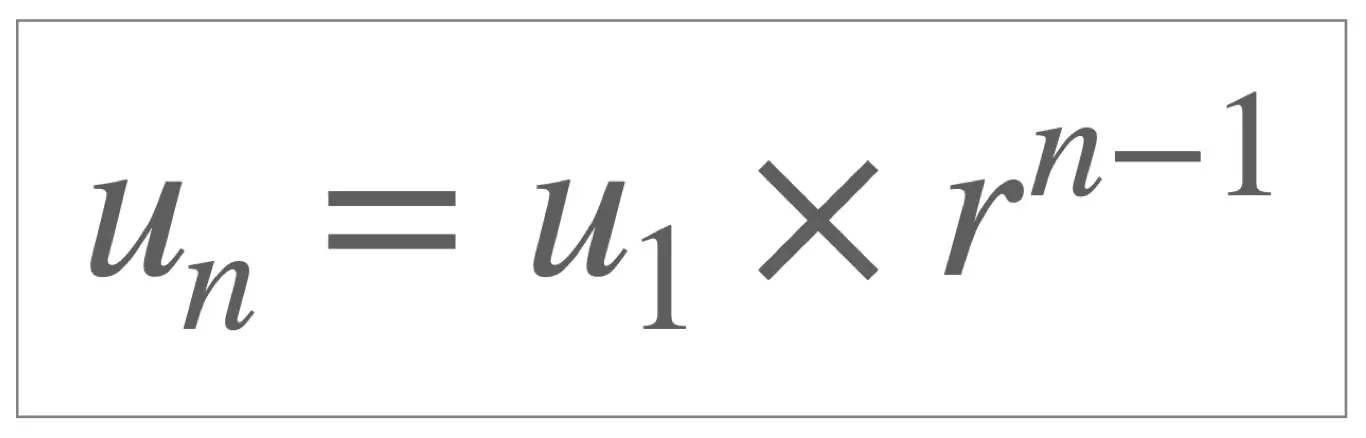
NOTE: given a geometric sequence, all we need to define the formula for n-th and therefore be able to calculate any term in the sequence is:

  • its first term \(u_1\)
  • its common ratio \(r\).

WORKED EXAMPLE 1

Given the following sequence of numbers: \[3, \ 6, \ 12, \ 24, \ 48, \ \dots \]

  1. Find its formula for the n-th term (formula for calculating any term).
  2. Calculate the 10th term.

Solution

  1. This is a geometric sequence whose common ratio is \(r = 2\); indeed to get from any one term to the next we always multiply by \(2\).

    To define this geometric sequence's n-th term all we need is:

    • the first term, which is \(u_1 = 3\)
    • the common ratio, which is \(r = 2\)
    replacing both \(u_1\) and \(r\) in the formula \(u_n = u_1.r^{n-1}\) leads to: \[u_n = 3\times 2^{n-1}\] Using this formula we can calculate any term of the sequence, all we have to do is replace every \(n\) we see inside the formula by the number of the term we wish to find.

  2. To calculate the 10-th term then we replace every \(n\) we see by \(10\), as shown here: \[\begin{aligned} u_{10} & = 3\times 2^{10-1} \\ & = 3\times 2^9 \\ & = 3\times 512 \\ u_{10} & = 1536 \end{aligned}\]

IB Students

For IB students: the formula for the n-th term of a geometric sequenice is given to you in the formula booklet.

Common Ratio Formula

Given an geometric sequence, we can find the common ratio, \(r\), by dividing any term in the sequence by its previous term.

This leads to the following recursive formula for \(r\):

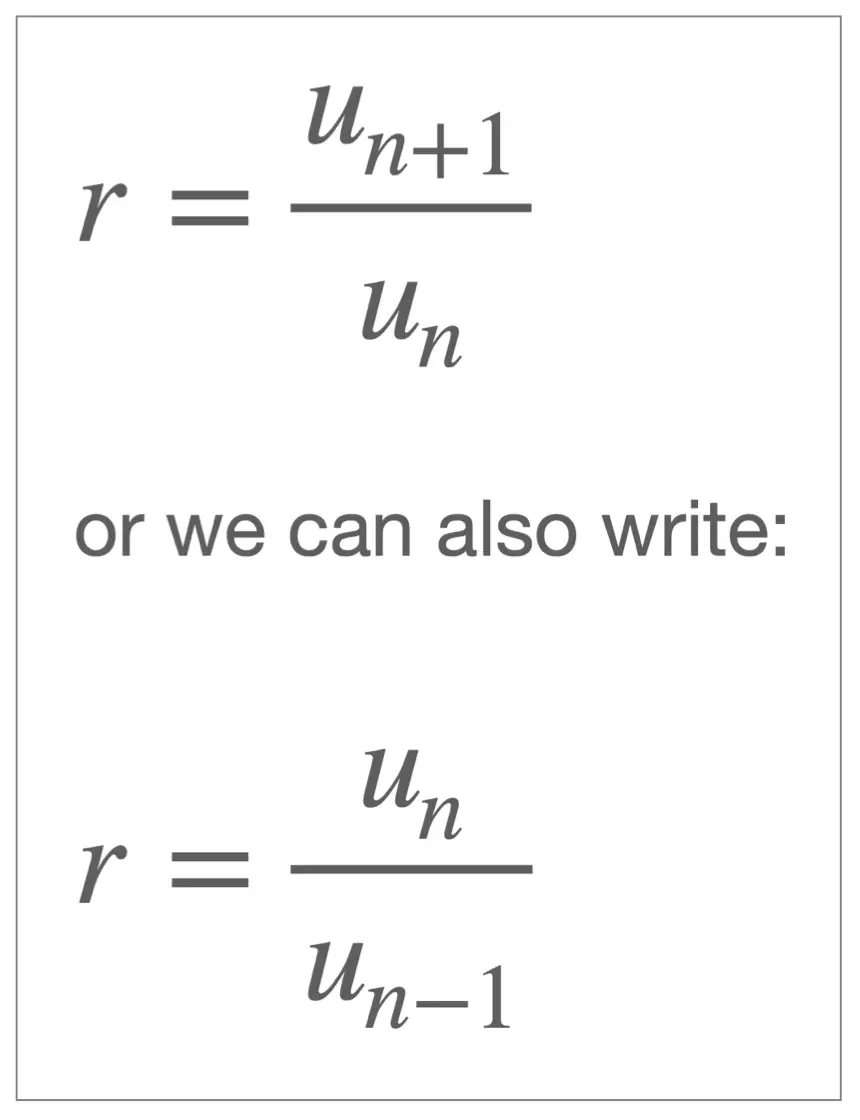
For example, given the arithmetic sequence: \[3,6,12,24,48,96, \dots \] we can calculate \(r\) using either of the following:

Using the first and second terms: \[ \begin{aligned} r & = \frac{u_2}{u_1} \\ & = \frac{6}{3} \\ r &=2 \end{aligned}\]
Using the second and third terms: \[\begin{aligned} r & = \frac{u_3}{u_2} \\ & = \frac{12}{6}\\ r & =2 \end{aligned}\]
Using the third and fourth terms: \[\begin{aligned} r &= \frac{u_4}{u_3} \\ & = \frac{24}{12} \\ r &= 2 \end{aligned}\]
More genrally we can write: \[r = \frac{u_2}{u_1} = \frac{u_3}{u_2} = \frac{u_4}{u_3} = \dots = \frac{u_n}{u_{n-1}} = \frac{u_{n+1}}{u_n}, \quad \forall n \in \mathbb{Z}^+ \]

WORKED EXAMPLE 2

The first few terms of a geometric sequence are shown here: \[6.25, \ 5, \ 4, \ 3.2, \ \dots \]

  1. Find the common ratio \(r\).
  2. State the formula for the n-th term.
  3. Rounding your answer to 3 significant figures, find \(u_{20}\).

Solution

  1. To find the common ratio we can use the formula \(r=\frac{u_{n+1}}{u_n}\). We can use any two consecutive terms but the easiest to work with seem to be \(u_3=4\) and \(u_5=5\). We can write: \[\begin{aligned} r & = \frac{u_3}{u_2} \\ & = \frac{4}{5} \\ r & = 0.8 \end{aligned}\] So the common ratio is \(r=0.8\)
  2. Using the fact that the formula for the n-th term of a geometric sequence is \(u_n = u_1\times r^{n-1}\), replacing \(u_1\) by \(6.25\) and \(r\) by \(0.8\) we get: \[u_n = 6.25 \times 0.8^{n-1}\]
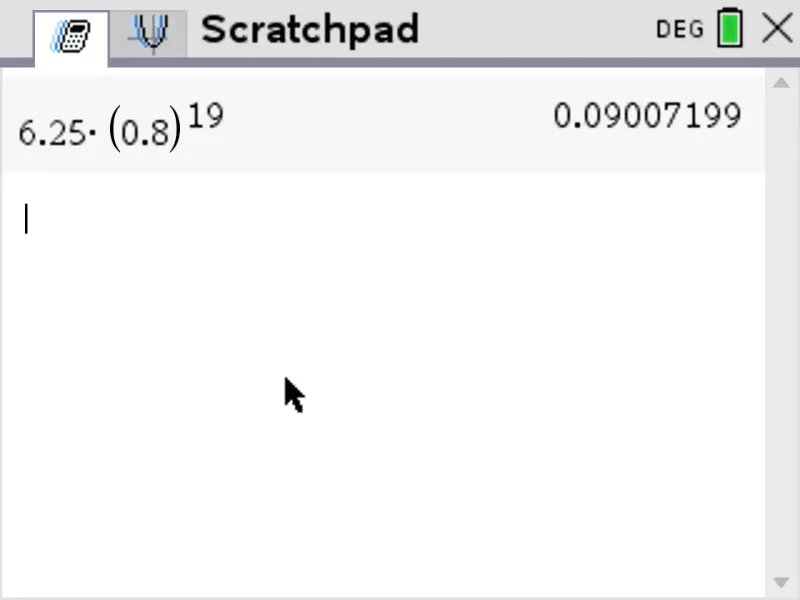  3. To calculate \(u_{20}\), the 20th term of the sequence, we replace \(n\) by \(20\) in our formula: \[\begin{aligned} u_{20} & = 6.25 \times 0.8^{20-1} \\ & = 6.25 \times 0.8^{19} \\ & = 0.090071992547413 \\ u_{20} & = 0.0901 \quad \text{(rounded to 3 significant figures)} \end{aligned}\]

The (Real) Formula for the General Term

Any 2 terms of a geometric sequence \(u_n\) and \(u_p\) the following result will always hold:

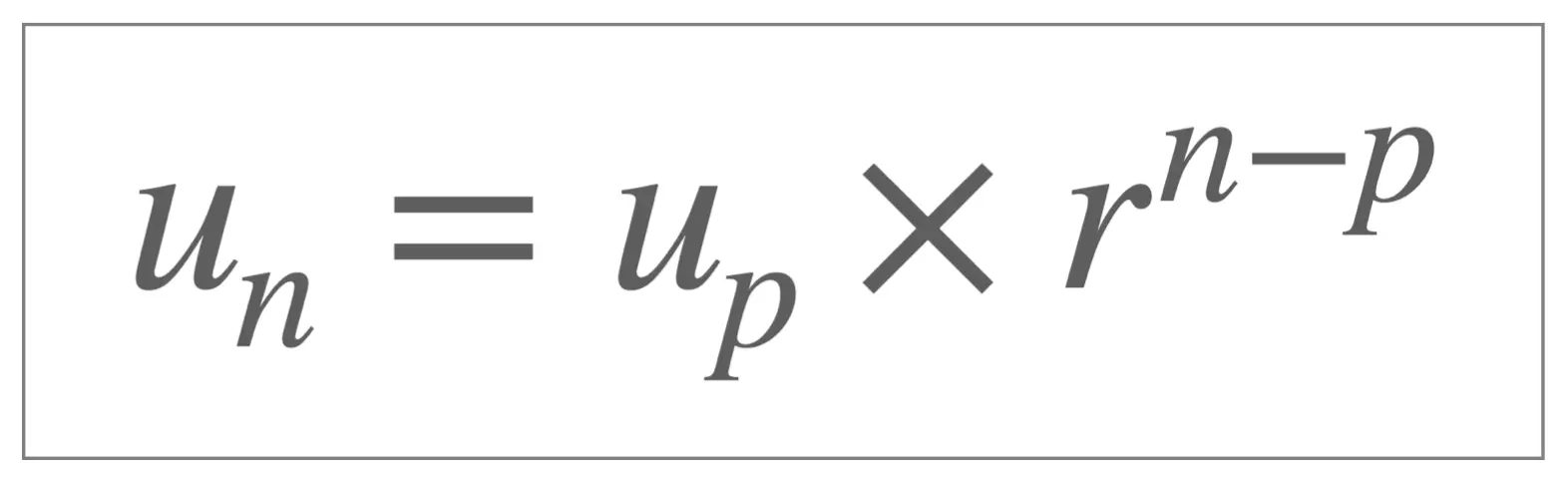
This formula allows us to calculate any term in the sequence provided we have any other term (not neccessarily \(u_1\)) and the common ratio.

Note: This formula can be particularly useful in exams and is often far more efficient than using the formula \(u_n = u_1 \times r^{n-1}\)

IB Students

Careful: this formula is not given in the formula booklet.

Worked Example 3

A geometric sequence has third term \(u_3=48\) and common ratio \(r=4\).

  1. Find \(u_7\).
  2. Find \(u_1\).

Worked Example 4

A geometric sequence has fourth term \(u_4=\) and common ratio \(r=4\).

  1. Find \(u_7\).
  2. Find \(u_1\).

GEOMETRIC SERIES

SUM of the first n terms of a Geometric Seuquence

GEOMETRIC SERIES (Sum of the first n terms of a Geometric Sequence)

Given a geometric sequence, such as: \[2, 6, 18, 54, 162, ... \] we can define its geometric series, which (for this geometric sequence) is the new sequence of numbers shown here: \[2, 8, 26, 80, 242, ... \] In this sequence of numbers the n-th term is equal to the sum of the first n terms of the geometric sequence we started-off with.

Sequences like this one are known as geometric series.

  • \(S_1 = u_1 = 3\)
  • \(S_2 = u_1 +u_2= 3 + 6 = 9\)
  • \(S_3 = u_1 +u_2 + u_3= 3 + 6 + 12= 21\)
  • \(S_4 = u_1 +u_2 + u_3 + u_4 = 3 + 6 + 12 + 24 = 45\)
  • \(\vdots \)
  • \(S_n = u_1 + u_2 + \dots + u_n\)
So, when we refer to the n-th term of the geometric series it is the same as referring to the sum of the first n terms of the geometric sequence teh series was made with.

Definition : Series

Given a sequence of numbers, the series that's associated to it is another sequence of numbers whose n-th term is equal to the sum of the first n terms of the sequence.

Tutorial: Geometric Series

In the following tutorial we learn the formula for calculating the sum of the first n terms of a geometric sequence and learn how to use it with a worked example.

Geometric Series : Formula for the n-th term

Given a geometric sequence with first term \(u_1\) and common ratio \(r\), we can calculate any term of its geometric series with either of the following formula:

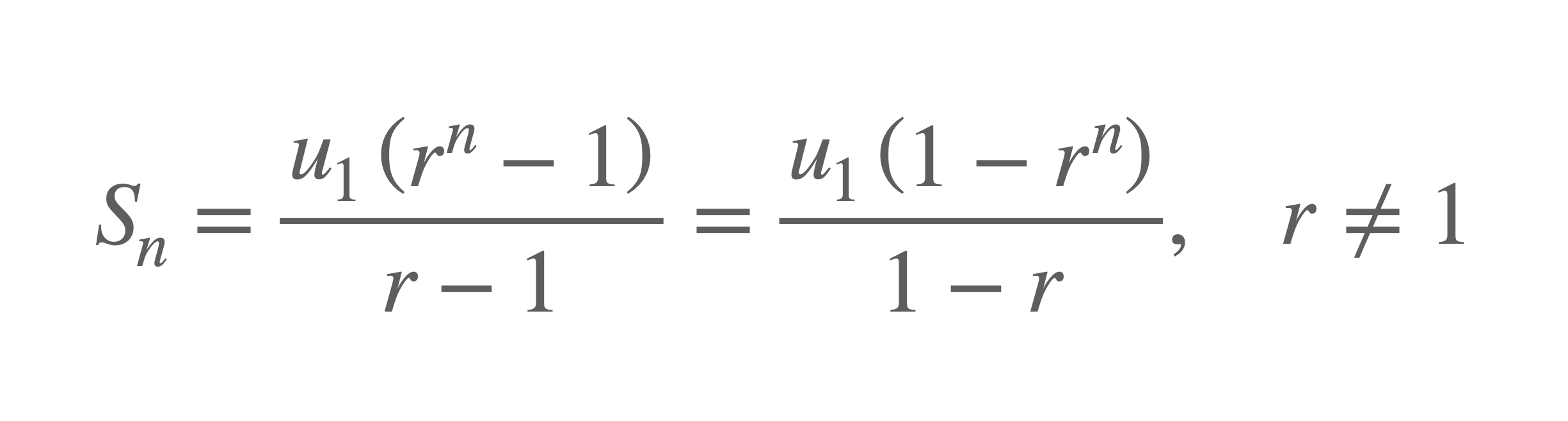
NOTE: given a geometric sequence, all we need to calculate the n-th term of its geometric series, and therefore the sum of its forst n terms, is:
  • its first term \(u_1\)
  • its common ratio \(r\).

Which Formula To Use?

Although there are two formula: it doesn't matter which of the two we use they'll both lead to the same result. BUT, when working with them by hand, to avoid having to handle negative numbers it's common practice to use the following rule:

  • if \( r < 1\) then we use \(S_n = \frac{u_1\begin{pmatrix}1-r^n\end{pmatrix}}{1-r}\)
  • if \( r > 1\) then we use \(S_n = \frac{u_1\begin{pmatrix}r^n-1\end{pmatrix}}{r-1}\)

IB Students

For IB students: the formula for the n-th term of a geometric sequenice is given to you in the formula booklet.

WORKED EXAMPLE 1

Given the following geometric sequence: \[3, \ 6, \ 12, \ 24, \ 48, \ \dots \]

  1. Calculate the sum of the first 10 terms.
  2. Calculate the sum of the first 20 terms.

Solution

This is a geometric sequence whose common ratio is \(r = 2\) and whose first term is \(u_1 = 3\).

Since the common ratio is greater than 1, \(r>1\), we'll use the formula \(S_n = \frac{u_1\begin{pmatrix}r^n-1\end{pmatrix}}{r-1}\).

  1. To calculate the sum of the first \(10\) terms we can use either of the two formula (stated above) replacing \(u_1\) by 3, \(r\) by \(2\) and \(n\) by \(10\): \[\begin{aligned} S_{10} & = \frac{u_1 \begin{pmatrix}r^{10}-1\end{pmatrix}}{r-1} \\ & = \frac{3\begin{pmatrix}2^{10}-1\end{pmatrix}}{2-1} \\ S_{10} & = 3069 \end{aligned}\] Note: When working with geometric series, more often than not, you'll be allowed to use your calculator.
  2. To calculate the sum of the first \(20\) terms we can use either of the two formula (stated above) replacing \(u_1\) by 3, \(r\) by \(2\) and \(n\) by \(20\): \[\begin{aligned} S_{20} & = \frac{u_1 \begin{pmatrix}r^{20}-1\end{pmatrix}}{r-1} \\ & = \frac{3\begin{pmatrix}2^{20}-1\end{pmatrix}}{2-1} \\ S_{20} & = 3145725 \end{aligned}\]

WORKED EXAMPLE 2

A geometric progression has first term \(96\) and third term \(24\).

  1. Given it's negative, find this sequence's common ratio \(r\).
  2. Rounding your answer to 3 significant figures, calculate the sum of this sequence's first 15 terms.

Solution

  1. To find the common ratio we use the fact that we know that the first term is 96, \(u_1=96\), and that the third term is 24, \(u_3 = 24\). Since we know that the n-th term of a geometric sequence is given by: \[u_n = u_1.r^{n-1}\] we can write: \[\begin{aligned} u_3 & = u_1.r^{3-1} \\ & = u_1.r^2 \\ u_3 & = 96 \times r^2 \end{aligned}\] Rearranging this we can make \(r^2\) the subject and solve for \(r\): \[\begin{aligned} r^2 & = \frac{24}{96} \\ r^2 & = \frac{1}{4} \\ r & \pm \sqrt{\frac{1}{4}} \\ r & \pm \frac{\sqrt{1}}{\sqrt{4}} \\ r & \pm \frac{1}{2} \\ \end{aligned}\] Finally, since we're told \(r<0\) we can state: \[r = - \frac{1}{2} = -0.5\]

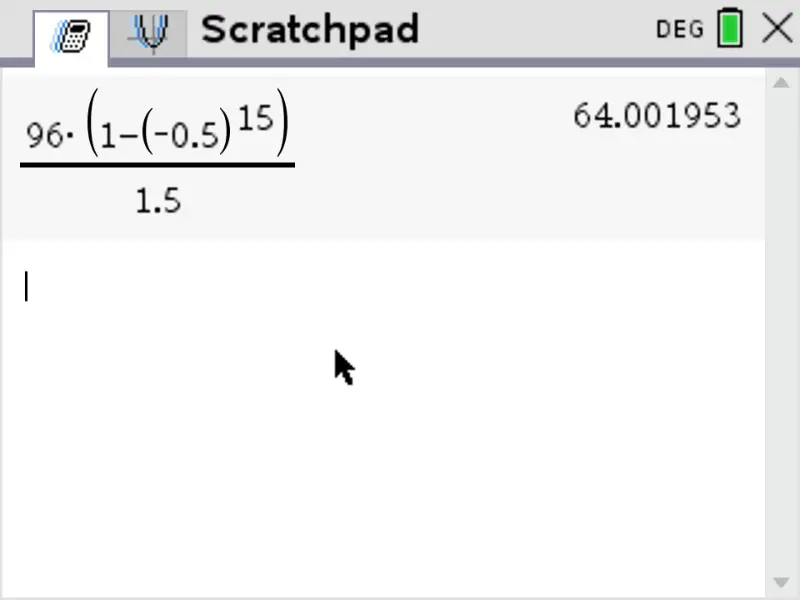  2. Since the common ratio is less than 1, \(r<1\) we'll use the \(S_n = \frac{u_1\begin{pmatrix}1-r^n\end{pmatrix}}{1-r}\); for that we replace \(u_1\) by \(96\) and \(r\) by \(-0.5\): \[\begin{aligned} S_{15} & = \frac{96\begin{pmatrix}1-(-0.5)^{15}\end{pmatrix}}{1- (-0.5)} \\ & = \frac{96\begin{pmatrix}1-(-0.5)^{15}\end{pmatrix}}{1+0.5} \\ & = \frac{96\begin{pmatrix}1-(-0.5)^{15}\end{pmatrix}}{1.5} \\ &= 64.001953124999 \\ S_{15} &= 64.0 \end{aligned}\]

WORKED EXAMPLE 3

The first two terms of a geometric sequence are \(u_1 = 3\) and \(u_2 = 3.15\).

  1. Find the value of \(r\).
  2. Find the least value of \(n\) such that \(S_n > 400\).

Solution

  1. We can find the common ratio \(r\) using the fact that: \[r = \frac{u_2}{u_1}\] This leads to: \[\begin{aligned} r & = \frac{u_2}{u_1} \\ & = \frac{3.15}{3} \\ r & = 1.05 \end{aligned}\] So this geometric sequence's common ratio \(r\) is \(r = 1.05\).

  2. Finding the least value of \(n\) such that \(S_n > 400\) is equivalent to finding the first value of \(n\) for which \(S_n > 400\).

    To answer this type of question we can follow 3 steps:

    • Step 1: find an expression for \(S_n\) in terms of \(n\), which we can do using our formula with \(u_1=3\) and \(r=1.05\): \[\begin{aligned} S_n & = \frac{u_1\begin{pmatrix}r^n - 1 \end{pmatrix}}{r-1} \\ & = \frac{3\begin{pmatrix}1.05^n - 1 \end{pmatrix}}{1.05-1} \\ S_n& = \frac{3\begin{pmatrix}1.05^n - 1 \end{pmatrix}}{0.05} \\ \end{aligned}\]
    • Step 2: we enter the equivalent function of \(x\) in our calculator. Here since our expression for \(S_n\) is \(S_n = \frac{3\begin{pmatrix}1.05^n - 1 \end{pmatrix}}{0.05}\), we enter the function \(f(x) = \frac{3\begin{pmatrix}1.05^x - 1 \end{pmatrix}}{0.05}\).
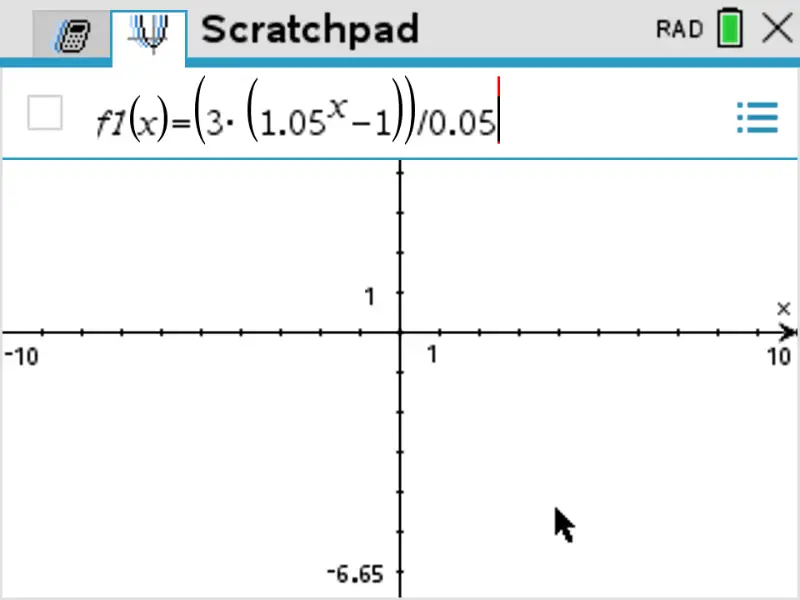
      Note: once you've entered the function make sure to press "enter" to make sure the function's graph is plotted; you needn't pay any attention to what the graph looks like though, move-on to step 3.
    • Step 3: use the table of values on the calculator to find the first integer value of \(x\) for which \(f(x)>400 \).
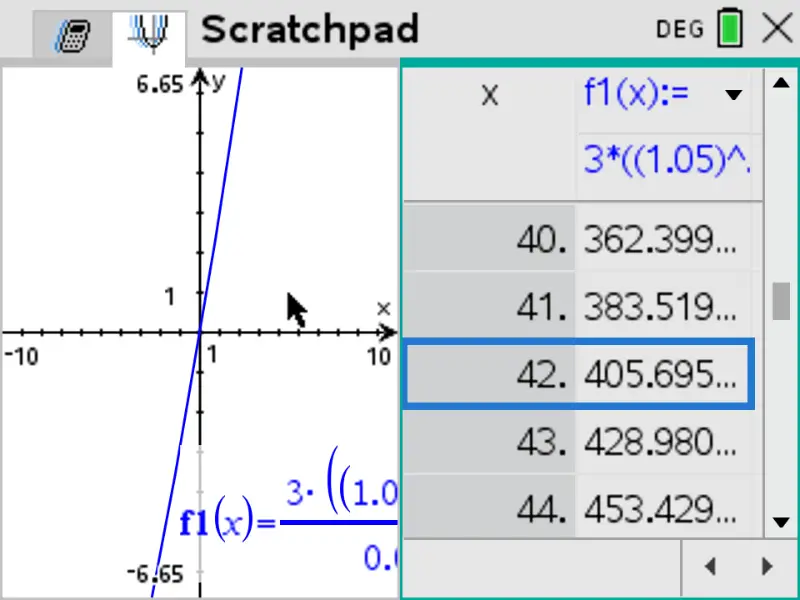
      Looking at the table of values we can see that:
      • when \(x=41\) : \(f(41) = 383.519...\)
      • when \(x=42\) : \(f(42) = 405.695...\)
      This tells us that for values of \(n\) greater than or equal to 42 : \(S_n\) is greater then 400. In a test/exam we could write:
      • \(S_{41} = 384\), rounded to 3 significant figures.
      • \(S_{42} = 406\), rounded to 3 significant figures.
      • \(S_{43} = 429\), rounded to 3 significant figures.
      • \(\vdots \)
      Finally, the least value of \(n\) such that \(S_n>400\) is \(42\), since \(S_{42}\) is the first value of the series to be greater than 400.


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.