Infinite Sum of a Geometric Sequence - Converging Geometric Series
If a geometric sequence's common ratio \(r\) lies between -1 and 1 then the sum of its terms will converge towards a finite number, known as its infinite sum, or total sum, which we'll refer to with the notation \(S_{\infty}\).
For example, consider the sequence : \[4, \ 2, \ 1, \ 0.5, \ 0.25, \ \dots \] This is a geometric sequence with \(u_1 = 4\) and \(r=0.5\)
Its corresponding geometric series is: \[4, \ 6, \ 7, \ 7.5, \ 7.75, \ \dots \] Remember: the n-th term of the geometric series is equal to the sum of the first n terms of the sequence.
As we add more and more terms of the sequence, their sum (and therefore the terms of the series) will get closer and closer to 8 but will never actually reach it.
Go ahead and try and try adding more terms of this sequence, you will never reach 8.
Nevertheless as we add more terms the sum will get closer and closer to 8, in fact it can get as close as we wish provided we add enough terms of the sequence. We say that the sum, and therefore the series, converges towards 8. We can write: \[\text{as} \ n \to +\infty, \ S_n \to S_{\infty}\] Where \(S_8 = 8\).
Infinite Sum : Converging Geometric Series Formula
Given a geometric sequence, if its common ratio is between -1 and 1: \[-1 < r < 1\] which we could also write: \[ \begin{vmatrix}r \end{vmatrix} < 1 \] then its corresponding geometric series converges (gets closer and closer) towards the "ininite sum" \(S_{\infty}\).

Tutorial: Infinite Sum - Full Lesson
This tutorial covers explains and illustrates the formula for the infinite sum as well as how and why it works.
Converging Geometric Series
When learning the formula for the sum of the first n terms of a geometric sequence, we had seen that given a geometric sequence, its geometric series is another sequence whose n-th term is equal to the sum of the first n terms of the sequence.
When we say that a geometric sequence has an infinite sum, a more rigorous way of saying this is that the sequence's corresponding geometric series converges towards a finite number, which we call the infinite sum and write \(S_{\infty}\).
Remember, the terms of the geometric series are defined as:
- \(S_1 = u_1\)
- \(S_2 = u_1+u_2\)
- \(S_3 = u_1+u_2+u_3\)
- \( \vdots \)
- \(S_n = u_1 + u_2 + \dots + u_n\)
Using sigma notation (sum notation) and limits, we can say that the series converges towards \(S_{\infty}\) as follows: \[\lim_{n \to \infty} S_n = \lim_{n \to \infty} \sum_{k=1}^n u_k = S_{\infty}\]
Infinite Sum : Converging Geometric Series Formula
Given a geometric sequence, if its common ratio is between -1 and 1: \[-1 < r < 1\] which we could also write: \[ \begin{vmatrix}r \end{vmatrix} < 1 \] then its corresponding geometric series converges (gets closer and closer) towards the "ininite sum" \(S_{\infty}\).

- its first term \(u_1\)
- its common ratio \(r\).
Tutorial: Sum of the First n Terms of a Geometric Sequence
In the following tutorial we learn the formula for calculating the sum of the first n terms of a geometric sequence and learn how to use it with a worked example.
WORKED EXAMPLE 1
Given the sequence of numbers : \[486, \ 162, \ 54, \ 18, \ 6, \ \dots \]
- State the value of this sequence's common ratio \(r\).
- State what allows us to confirm this sequence has an infinite sum.
- Rounding your answer to 2 decimal places, calculate the sum of the this sequence's first 10 terms.
- Calculate the infinite sum.
Solution
- This sequence's common ratio is \(r=\frac{1}{3}\).
- Since \( -1 < r < 1\), indeed \( -1 < \frac{1}{3} < 1\), we can state without further justification that this sequence has an infinite sum.
-
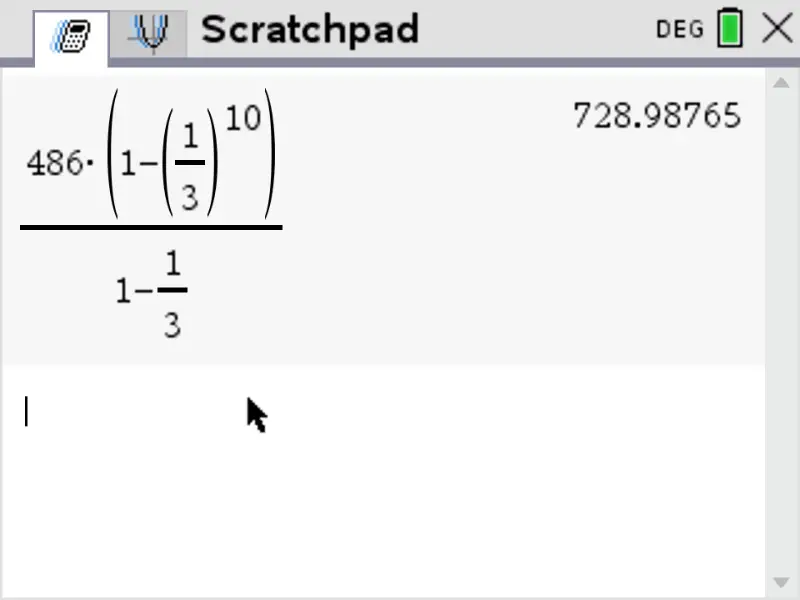 To calculate the sum of the first \(10\) terms, we use the formula for the sum of the first \(n\) terms, \(S_n\), to write:
\[\begin{aligned}
S_{10} & = \frac{u_1\begin{pmatrix}1-r^{10}\end{pmatrix}}{1-r} \\
& = \frac{486 \begin{pmatrix}1-\begin{pmatrix}\frac{1}{3}\end{pmatrix}^{10}\end{pmatrix}}{1-\frac{1}{3}} \\
& = \frac{486 \begin{pmatrix}1 - \begin{pmatrix}\frac{1}{3}\end{pmatrix}^{10}\end{pmatrix}}{\frac{2}{3}} \\
& = 728.98765432098 \\
S_{10} & = 728.99 \quad \text{(rounded to 2 dp)}
\end{aligned}\]
To calculate the sum of the first \(10\) terms, we use the formula for the sum of the first \(n\) terms, \(S_n\), to write:
\[\begin{aligned}
S_{10} & = \frac{u_1\begin{pmatrix}1-r^{10}\end{pmatrix}}{1-r} \\
& = \frac{486 \begin{pmatrix}1-\begin{pmatrix}\frac{1}{3}\end{pmatrix}^{10}\end{pmatrix}}{1-\frac{1}{3}} \\
& = \frac{486 \begin{pmatrix}1 - \begin{pmatrix}\frac{1}{3}\end{pmatrix}^{10}\end{pmatrix}}{\frac{2}{3}} \\
& = 728.98765432098 \\
S_{10} & = 728.99 \quad \text{(rounded to 2 dp)}
\end{aligned}\]
- The infinite sum is calculated with the formula: \[S_{\infty} = \frac{u_1}{1-r}\] For this sequence this leads to: \[\begin{aligned} S_{\infty} &= \frac{u_1}{1-r} \\ & = \frac{486}{1 - \frac{1}{3}} \\ & = \frac{486}{\frac{2}{3}} \\ & = 486 \times \frac{3}{2} \\ S_{\infty} & = 729 \end{aligned} \]
WORKED EXAMPLE 2
A geometric sequence has a first term \(u_1 = 8\) and an infinite sum \(S_{\infty} = 20\).
Find this sequence's common ratio.
Solution
We know that this sequence has an infinite sum \(S_{\infty} = 20\), in other words we know that the sum of its terms converges towards \(20\).
Furthermore, we're given this sequences's first term \(u_1 = 8\). Consequently we can use the infinite sum formula to write: \[S_{\infty} = \frac{u_1}{1-r}\] Now replacing \(u_1\) by \(8\) and \(S_{\infty}\) by \(20\) we obtain an equation for the unknown common ratio \(r\): \[20 = \frac{8}{1-r}\] To find \(r\) we start by getting away from the denominator, which we do by multiplying both sides of this equation by \(\begin{pmatrix}1-r \end{pmatrix}\): \[20\begin{pmatrix}1-r \end{pmatrix} = 8\] Now that \(r\) is away from the numerator, we can solve the usual way: \[\begin{aligned} & 20 - 20r = 8 \\ & -20r = 8-20 \\ & -20r = -12 \\ & r = \frac{-12}{-20} \\ & r = \frac{-4 \times 3}{-4 \times 5} \\ & r = \frac{3}{5} \quad \begin{pmatrix}r = 0.6 \end{pmatrix} \end{aligned}\]
WORKED EXAMPLE 3
A geometric sequence is such that its third term is \(u_3 = 3.2\), its common ratio is such that \(r>0.6\) and it has an infinite sum equal to \(S_{\infty}=25\).
Find the values of this sequence's first term \(u_1\) and its common ratio \(r\).
Solution
In this example there are 2 unknowns to find, namely \(u_1\) and \(r\).
This suggests we need 2 distinct equations involving \(u_1\) and \(r\), which we can then solve simultaneously.
To obtain the 2 equations we use the 2 bits of information we're given. This is done as follows:
- We're told that \(u_3=3.2\) and we know that \(u_3 = u_1r^2\). Combining these two results leads to our first equation invvoling the two unknowns we're after: \[3.2 = u_1r^2 \quad \text{: (E1)}\]
- We're told that \(S_{\infty} = 25\) and we know that \(S_{\infty} = \frac{u_1}{1-r}\). Combining these two results leads to a second equation involving the two unknows we're after: \[25 = \frac{u_1}{1-r} \quad \text{: (E2)} \]
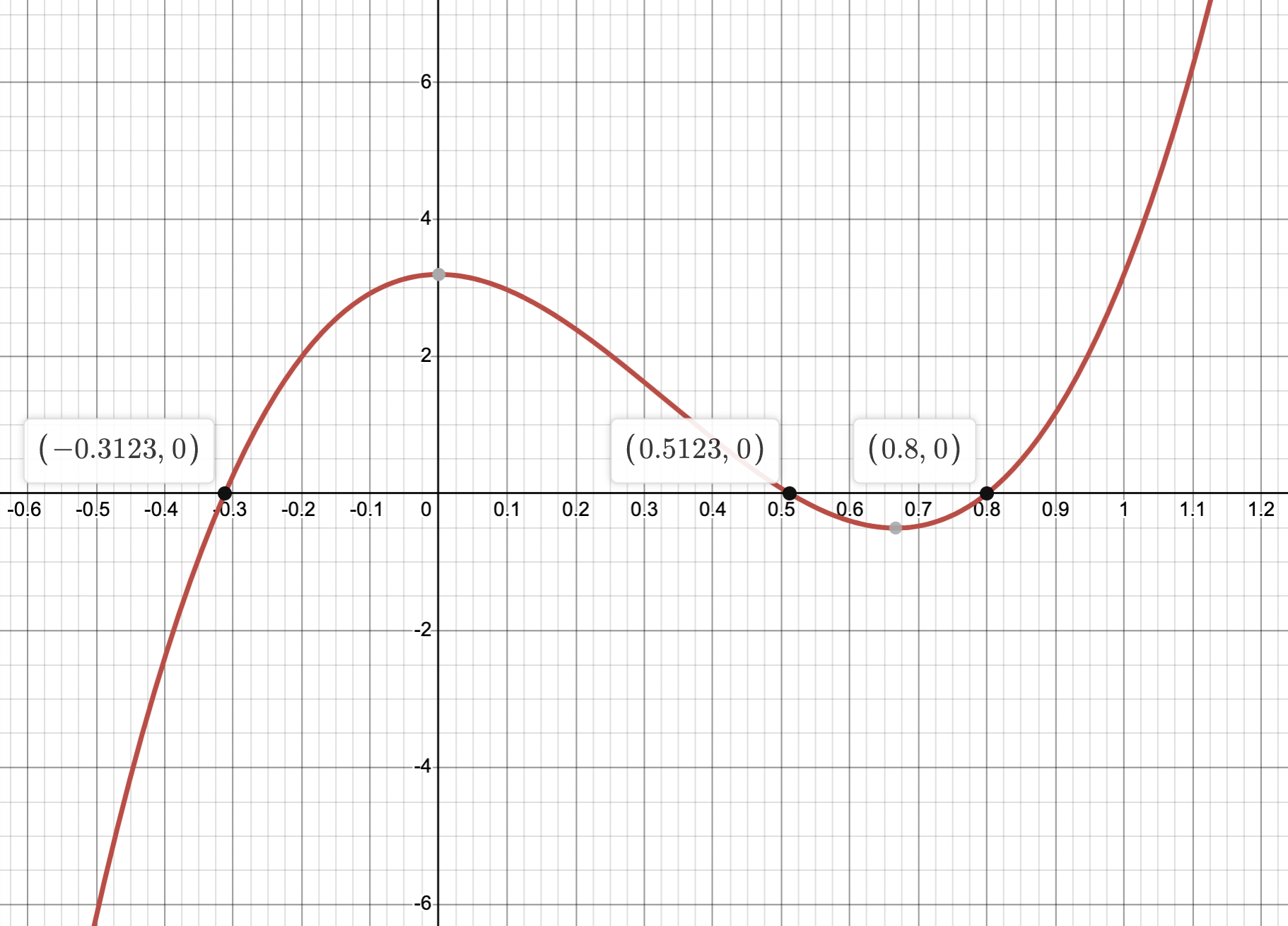
We can solve this equation graphically by looking for the values of x at which the curve \(y = 25x^3-25x^2+3.2\) cuts the x-axis.
We can see that there are 3 values of x at which that happens: \[x = -0.3123, \ x = 0.5123, \ \text{and} \ x = 0.8\] Since we were told that \(r > 0.6\) the value of \(r\) we're looking for must therefore be: \[r = 0.8\]
\(y = 25x^3-25x^2+3.2\) and its x-intercepts
Now that we know that \(r=0.8\) we can go back to (E2), which was \(u_1 = 25\begin{pmatrix}1-r\end{pmatrix}\), and replace \(r\) by \(0.8\) to find \(u_1\): \[\begin{aligned} u_1 & = 25\begin{pmatrix}1-r \end{pmatrix} \\ & = 25\begin{pmatrix} 1 - 0.8 \end{pmatrix} \\ & = 25 \begin{pmatrix}0.2 \end{pmatrix} \\ u_1 & = 5 \end{aligned}\]
Finally we can state our answers as:
- the first term is \(u_1 = 5\)
- the common ratio is \(r = 0.8\).
Scan this QR-Code with your phone/tablet and view this page on your preferred device.
Subscribe Now and view all of our playlists & tutorials.