Simultaneous Equations - Quadratic & Linear
Intersection: Parabola and a Line - Circle and a Line
In this section we learn how to solve simultaneous equations involving quadratics and linears.
For example, by the end of this section we'll know how to solve either of the following pair of simultaneous equations:
Scenario 1: Parabola & Straight Lines
Scenario 2: Cirlces & Straight Lines
Scenario 1: Intersection of a Parabola and a Line
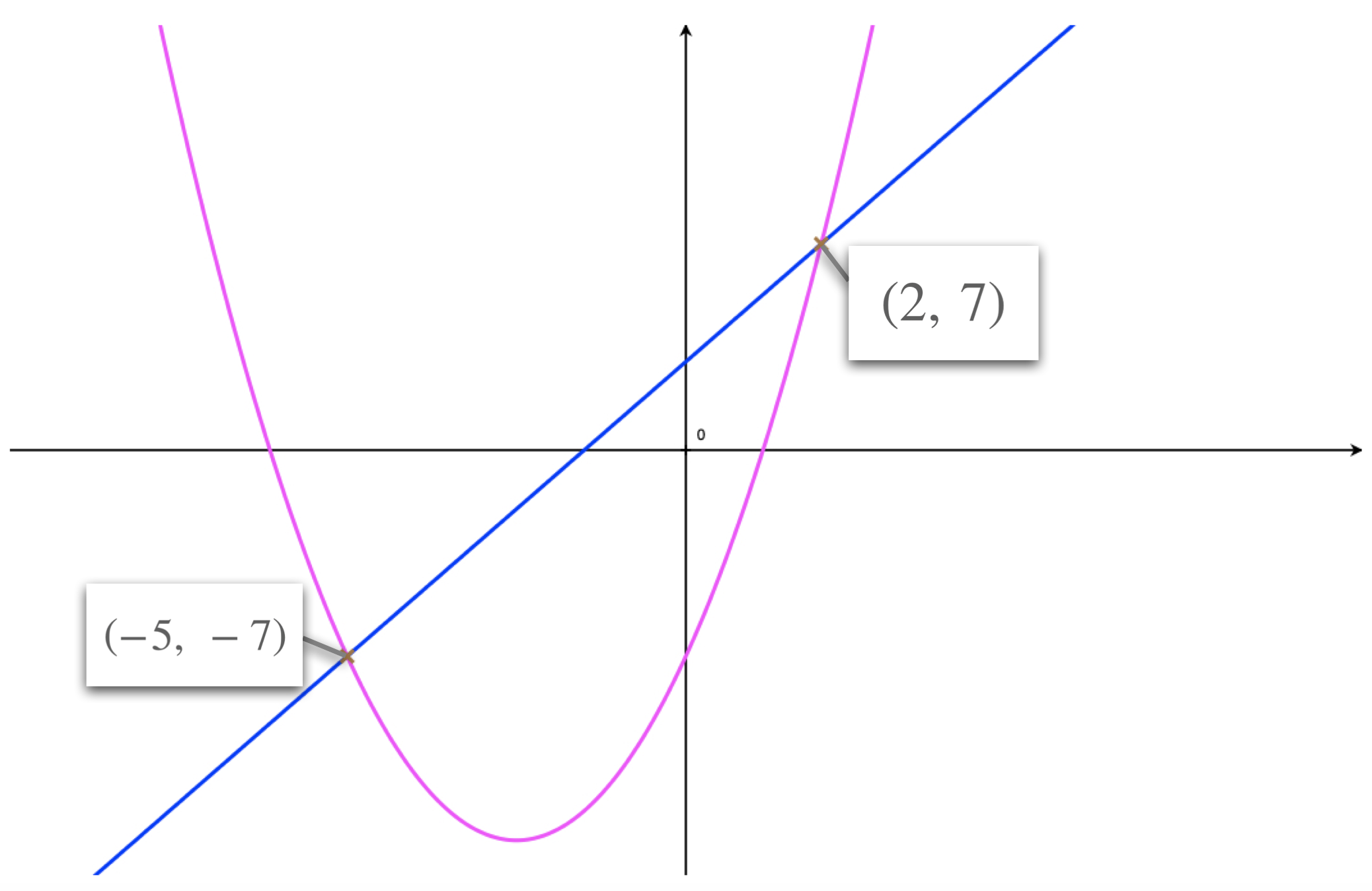
In this first section we learn how to solve simultaneous equations such as: \[\begin{aligned} & y = x^2 + 5x - 7 \\ & y = 2x + 3 \end{aligned}\] The method used is the method of substitution.
When solving such simultaneous equations we're finding the coordinates (\(x\) and \(y\)) of the point(s) of intersection of a parabola and a line.
Illustration: Intersection of a Parabola and a Line

The method for solving such simultaneous equations, and therefore for finding the coordinates of the point(s) of intersection of a parabola and a line, is shown in the following tutorials.
Example 1: Quadratic & Linear Simultaneous Equation
(Intersection of a Parabola & Straight Line)
In this example we solve the following pair of simultaneous equations: \[\begin{aligned} & y = x^2 + 5x - 7 \\ & y = 2x + 3 \end{aligned}\]
Example 2: Quadratic & Linear Simultaneous Equation
(Intersection of a Parabola & Straight Line)
In this example we solve the following pair of simultaneous equations: \[\begin{aligned} & y = x^2 + 4x - 9 \\ & 2x - y = 6 \end{aligned}\]
Scenario 2: Intersection of a Circle and a Line
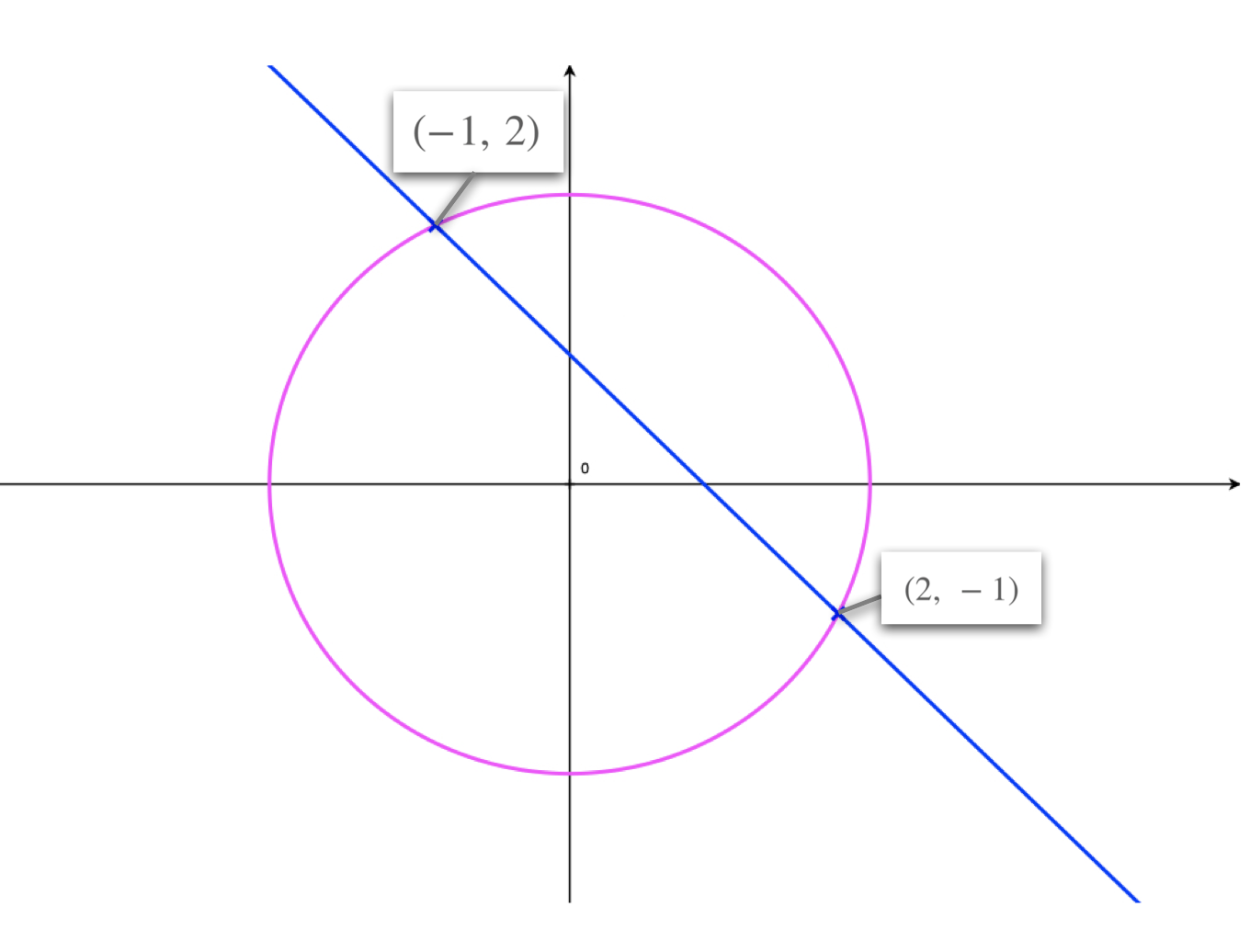
We now learn how to solve simultaneous of the type: \[\begin{aligned} & x^2+y^2 = 5 \\ & x + y = 1 \end{aligned} \] Again, we use the method of substtution.
When solving this type of pair of simultaneous equations we're finding the coordinates (\(x\) and \(y\)) of the point(s) of intersection of a circle and a line.
Illustration: Intersection of a Circle and a Line

The method for solving such simultaneous equations, and therefore finding the coordinates of the point(s) of intersection of a circle and a straight line, is explained in the following tutorial.
Example 3: Quadratic & Linear Simultaneous Equation
(Intersection of a Circle & Straight Line)
In this example we solve the following pair of simultaneous equations: \[\begin{aligned} & x^2 + y^2 = 5 \\ & x + y = 1 \end{aligned}\]
Scan this QR-Code with your phone/tablet and view this page on your preferred device.
Subscribe Now and view all of our playlists & tutorials.