Stationary Points - Part 2
(how the sign of the derivative changes near a maximum, minimum, or horizontal point of inflection)
We know, from the previous section that at a stationary point the derivative function equals zero, \(\frac{dy}{dx} = 0\). But on top of knowing how to find stationary points, it is important to know how to classify them, that is to know how to determine whether a stationary point is a maximum, a minimum, or a horizontal point of inflexion.
The Sign of the Derivative
What allows us to distinguish the different types of stationary points is the sign of the derivative, \(\frac{dy}{dx}\), on either side (left or right) of the stationary point.
Maximum Points
As we move along a curve, from left to right, past a maximum point we'll always observe the following:
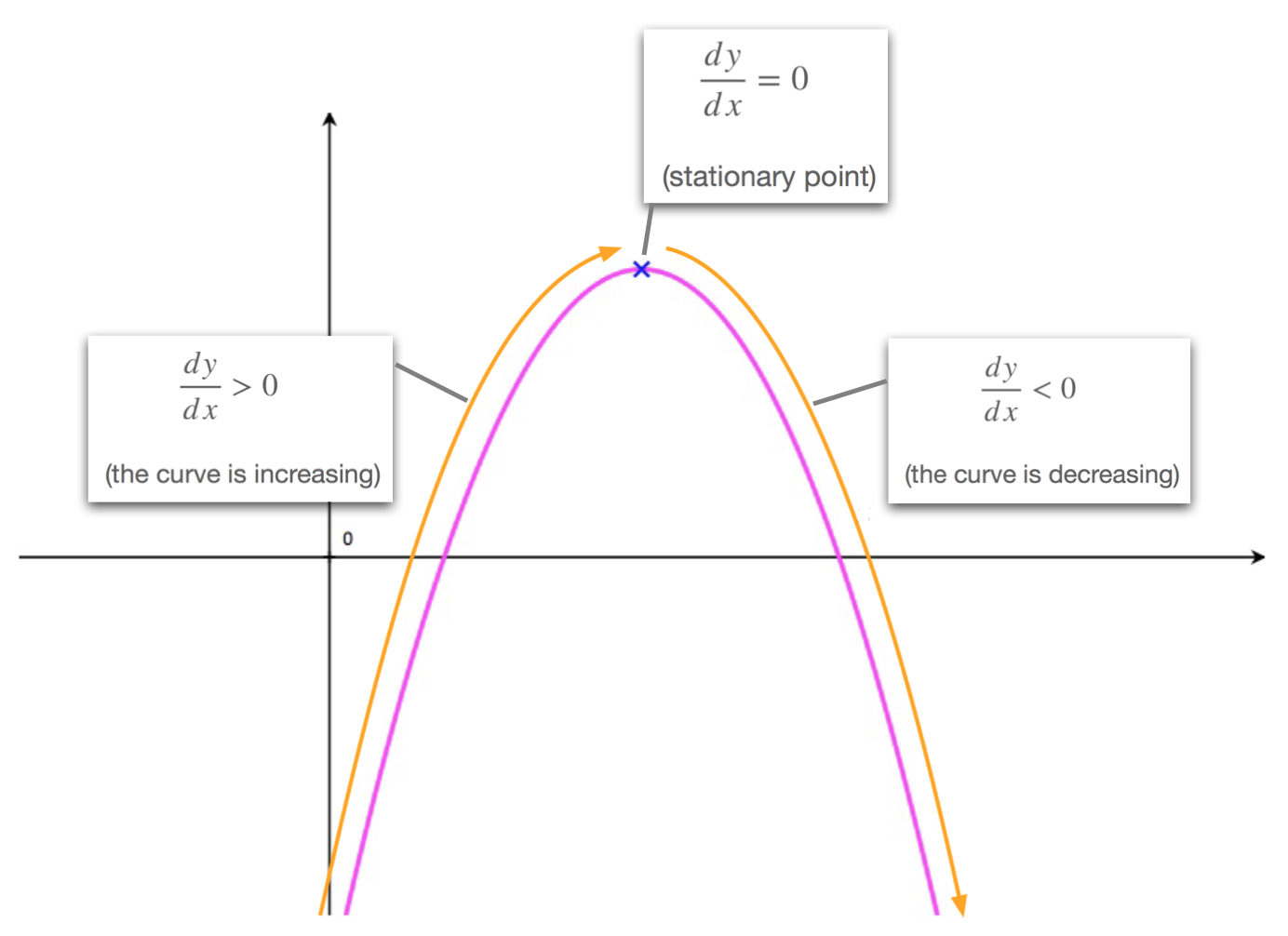
- as we approach the maximum, from the left hand side, the curve is increasing (going higher and higher). Consequently the derivative is positive: \(\frac{dy}{dx}>0\).
- when we reach the maximum point, the gradient equals to zero. This is a stationary point and therefore: \(\frac{dy}{dx}=0\).
- as we leave the maximum, moving towards the right, the curve is decreasing. Consequently the derivative is negative: \(\frac{dy}{dx}<0\).
| to the left of a maximum point | at a maximum point | to the right of a maximum point |
| \(\frac{dy}{dx}>0\) | \(\frac{dy}{dx}=0\) | \(\frac{dy}{dx}< 0\) |
Minimum Points
As we move along a curve, from left to right, past a minimum point we'll always observe the following:
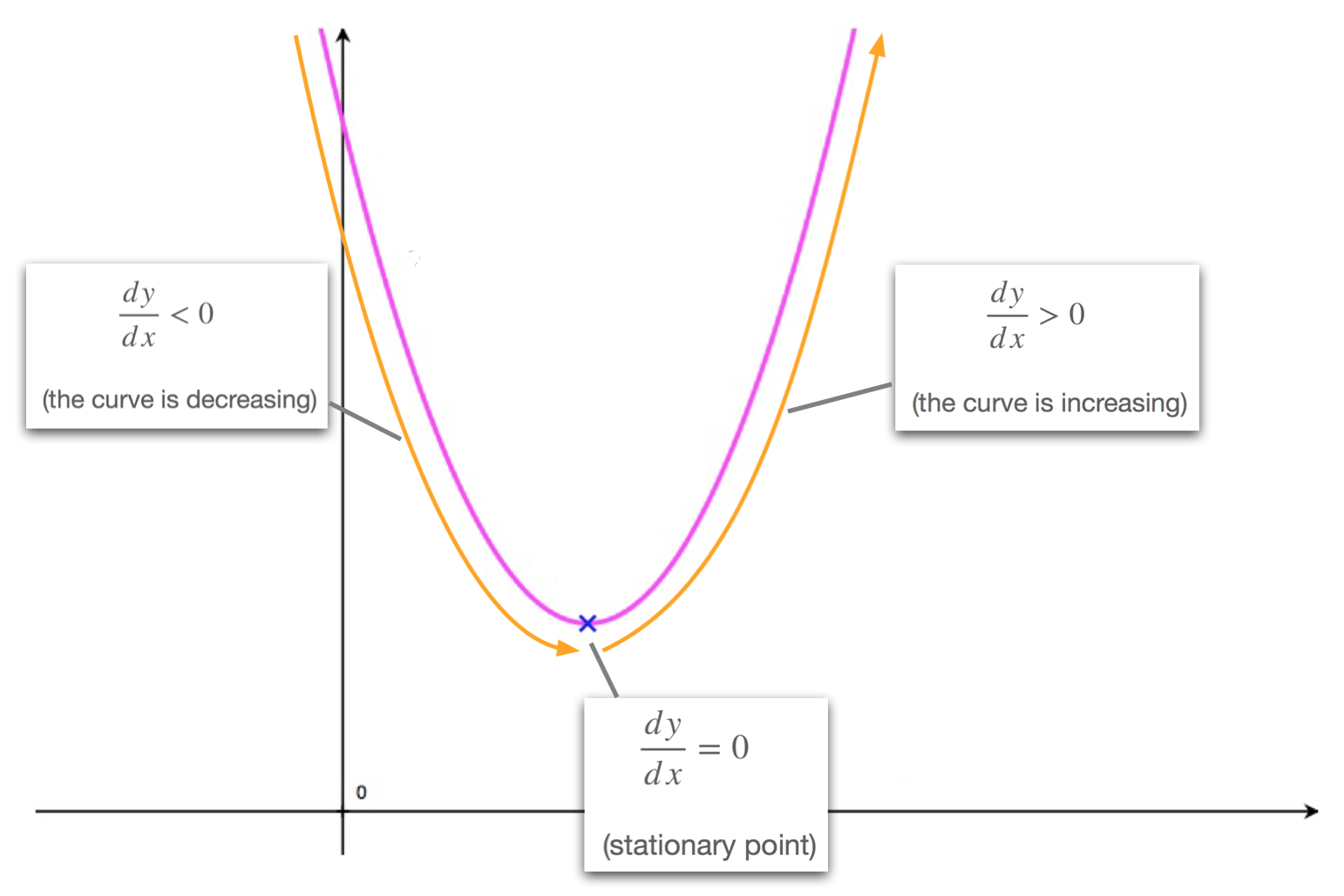
- as we approach the minimum, from the left hand side, the curve is decreasing. Consequently the derivative is negative: \(\frac{dy}{dx}<0\).
- when we reach the minimum point, the gradient equals to zero. This is a stationary point and therefore: \(\frac{dy}{dx}=0\).
- as we leave the minimum, moving towards the right, the curve is increasing. Consequently the derivative is positive: \(\frac{dy}{dx}>0\).
| to the left of a minimum point | at a minimum point | to the right of a minimum point |
| \(\frac{dy}{dx}<0\) | \(\frac{dy}{dx}=0\) | \(\frac{dy}{dx}> 0\) |
Horizontal Points of Inflection
There are two types of horizontal points of inflection, increasing and decreasing. We discuss both here.
Increasing Horizontal Point of Inflection
As we move along a curve, from left to right, past an increasing horizontal point of inflection we'll always observe the following:

- as we approach the increasing horizontal point of inflection, from the left hand side, the curve is increasing. Consequently the derivative is positive: \(\frac{dy}{dx}>0\).
- when we reach the increasing horizontal point of inflection, the gradient equals to zero. This is a stationary point and therefore: \(\frac{dy}{dx}=0\).
- as we leave the increasing horizontal point of inflection, moving towards the right, the curve is increasing. Consequently the derivative is positive again: \(\frac{dy}{dx}>0\).
| to the left of a increasing horizontal point of inflection | at a increasing horizontal point of inflection | to the right of a increasing horizontal point of inflection |
| \(\frac{dy}{dx}>0\) | \(\frac{dy}{dx}=0\) | \(\frac{dy}{dx}> 0\) |
Decreasing Horizontal Point of Inflection
As we move along a curve, from left to right, past an decreasing horizontal point of inflection we'll always observe the following:
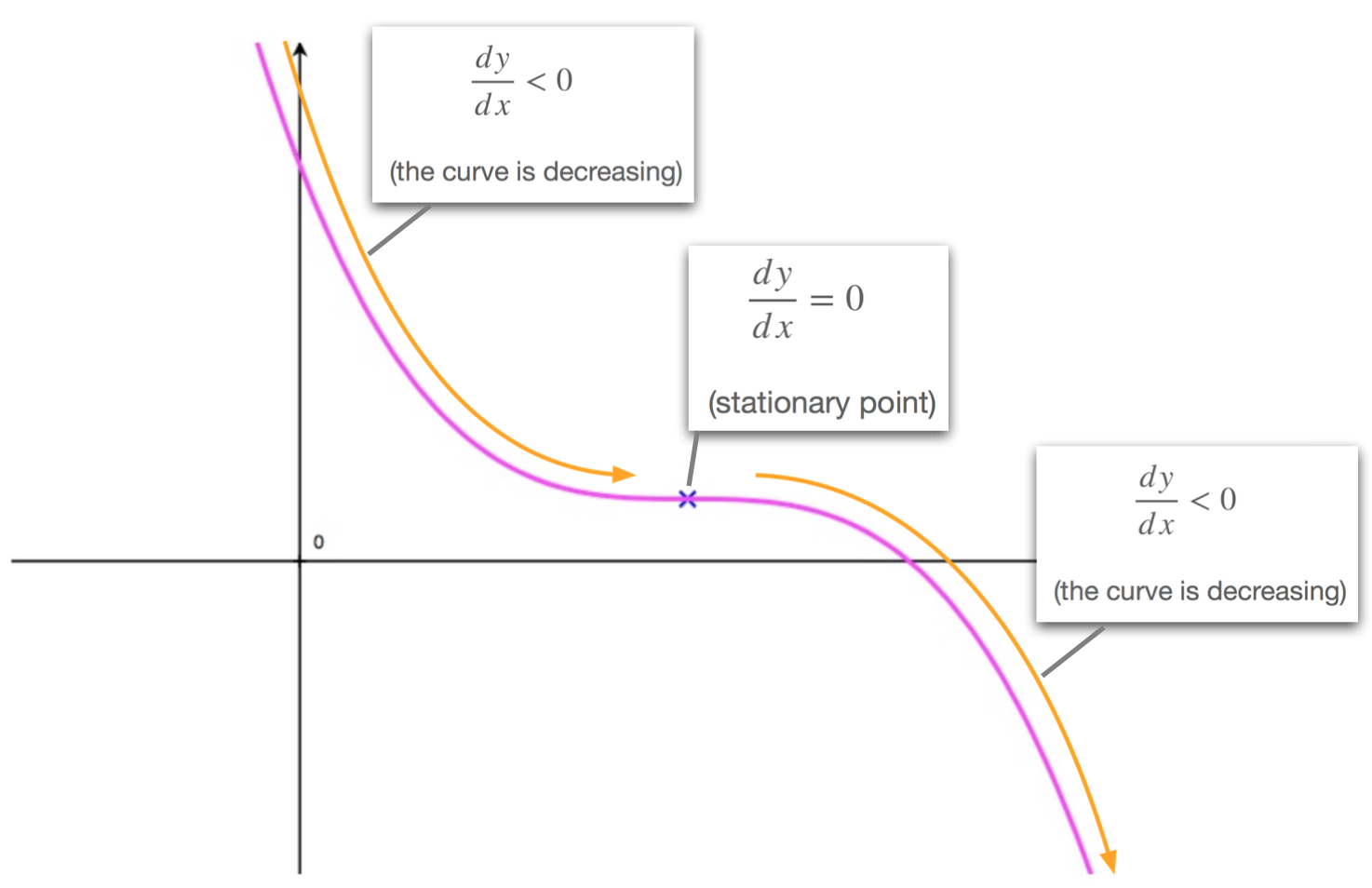
- as we approach the decreasing horizontal point of inflection, from the left hand side, the curve is decreasing. Consequently the derivative is negative: \(\frac{dy}{dx} < 0\).
- when we reach the decreasing horizontal point of inflection, the gradient equals to zero. This is a stationary point and therefore: \(\frac{dy}{dx}=0\).
- as we leave the decreasing horizontal point of inflection, moving towards the right, the curve is decreasing. Consequently the derivative is negative again: \(\frac{dy}{dx} < 0\).
| to the left of a decreasing horizontal point of inflection | at a decreasing horizontal point of inflection | to the right of a decreasing horizontal point of inflection |
| \(\frac{dy}{dx}<0\) | \(\frac{dy}{dx}=0\) | \(\frac{dy}{dx}< 0\) |