Transformed Cosine & Sine Curves - Wave Function
(Working with Degrees)
Transformed cosine and sine curves, sometimes called wave functions, are cosine and sine curves on which we have carried-out a series of transformations.
In their most general form, wave functions are defined by the equations: \[y = a.cos\begin{pmatrix}b(x-c)\end{pmatrix}+d\]
- \(a\) is known as the amplitude
- \(b\) is known as the wave number, also called the angular frequency
- \(c\) is known as the phase shift
- \(d\) is known as the vertical shift or rest position.
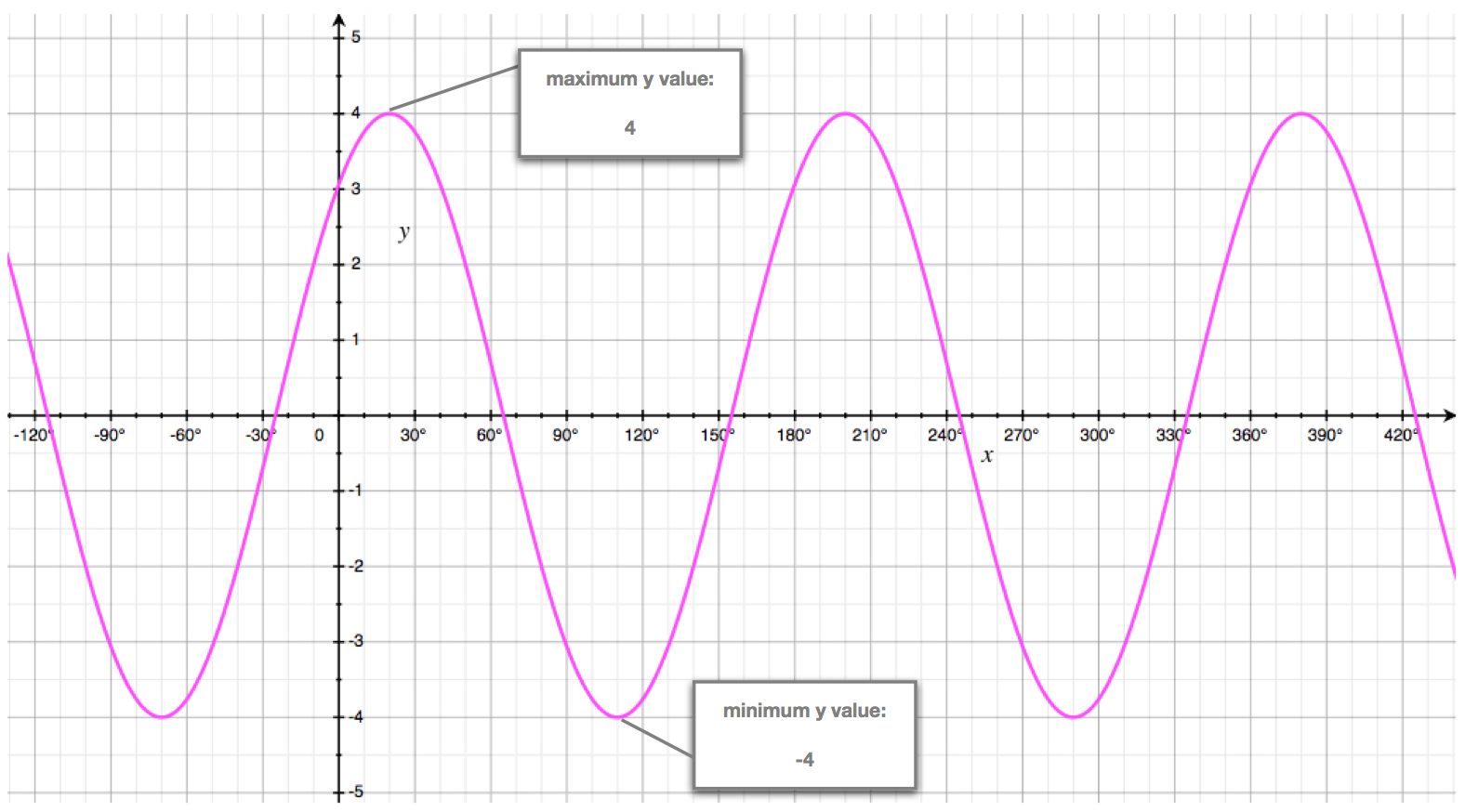
By the end of this, we should be quite comfortable with any cosine or sine curve looking like the one shown here:
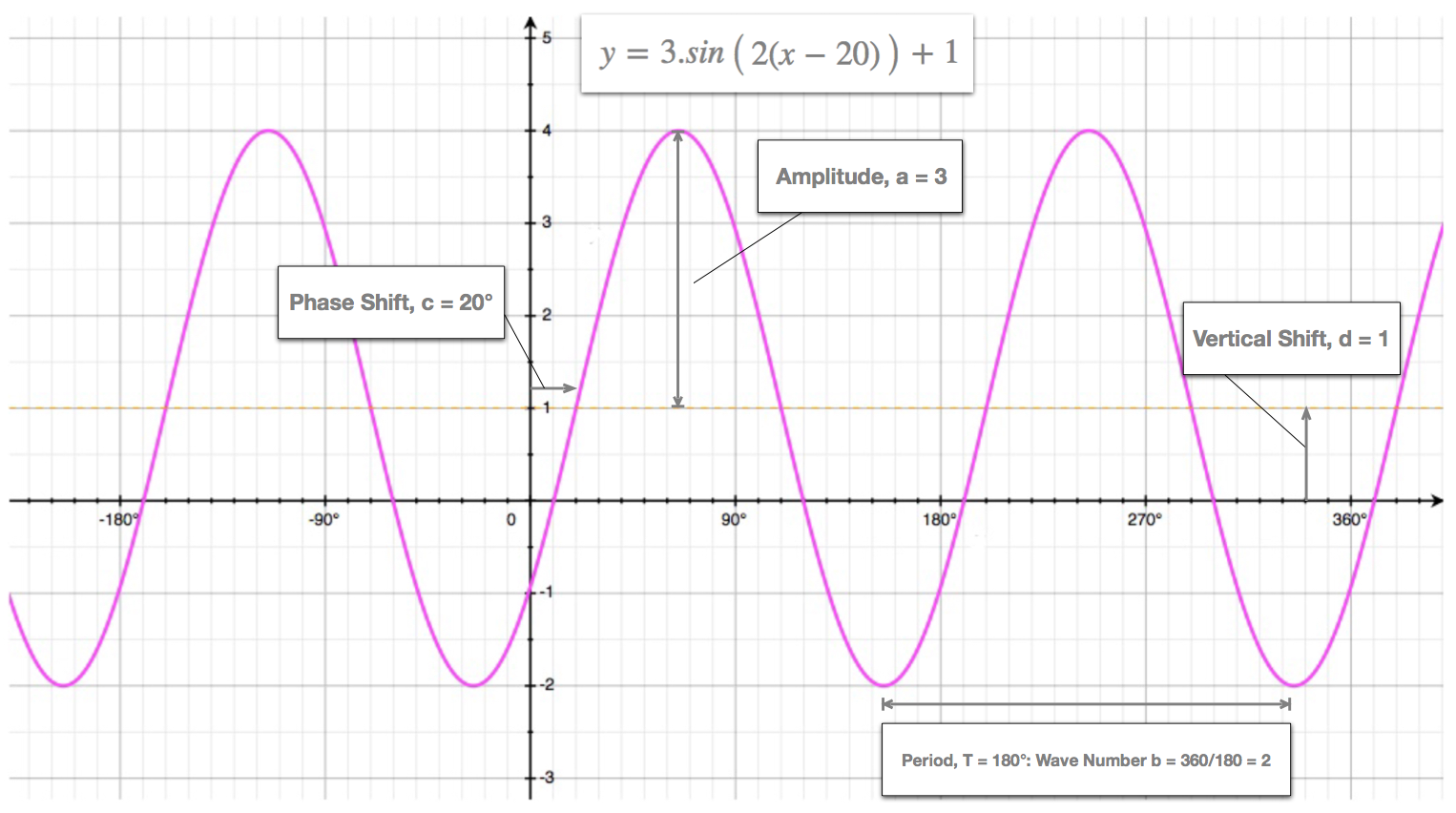
The Amplitude: \(a\)
The amplitude of a cosine, or a sine, curve is the amount by which the curve oscillates (either above or below) its "rest", or mean, value.
The amplitude is illustrated here. The pink curve is: \[y = 3.cos(x)\] The dotted curve is the "regular" \(y = cos(x)\) curve.
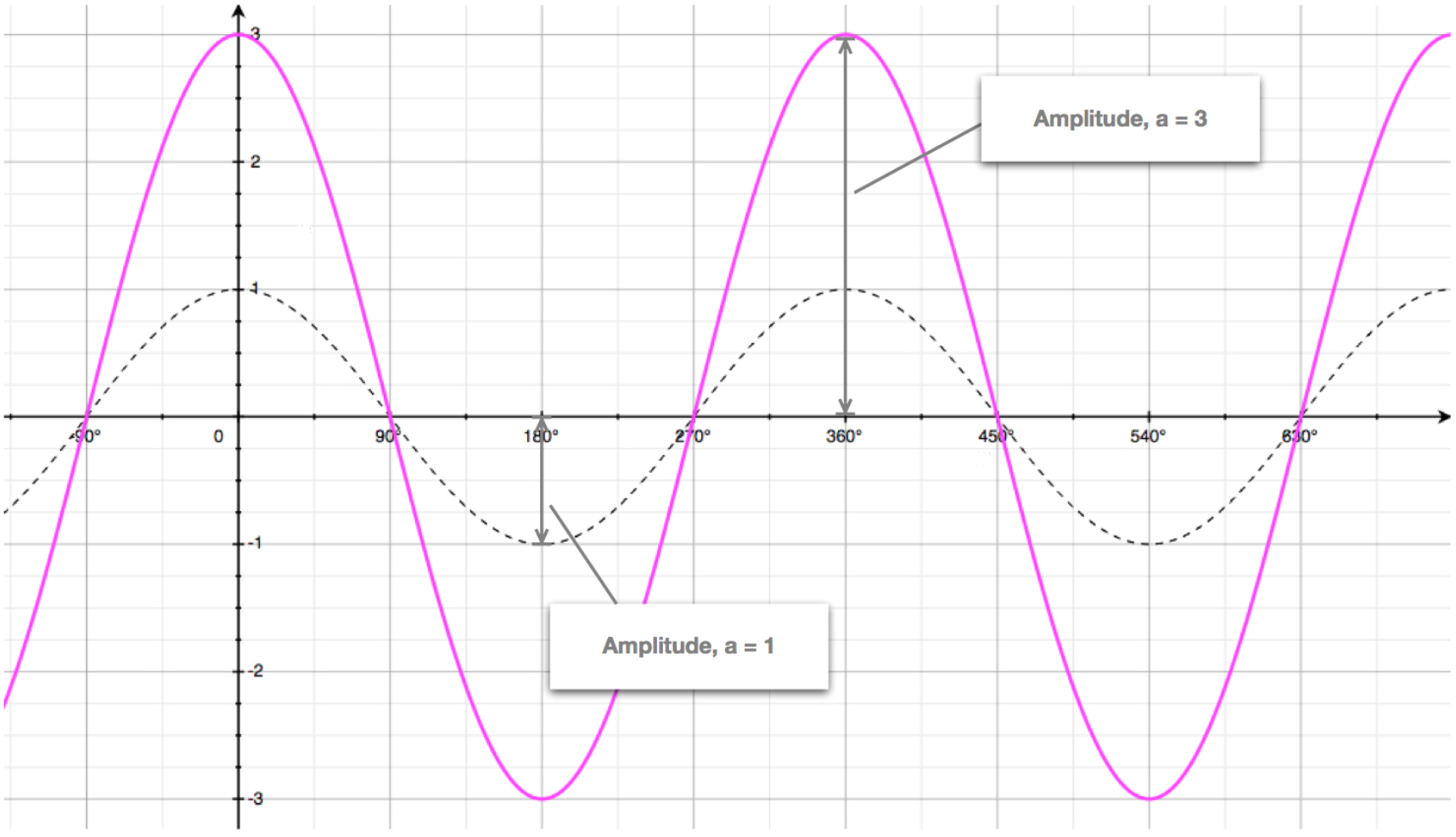
We can see that:
- the pink curve \(y=3.cos(x)\) oscillates \(3\) units either side of the \(x\)-axis, it has an amplitude of \(3\): \(a = 3\).
- the dotted curve \(y=cos(x)\) oscillates \(1\) unit either side of the \(x\)-axis, it has an amplitude of \(1\): \(a = 1\).
Formula for amplitude \(a\)
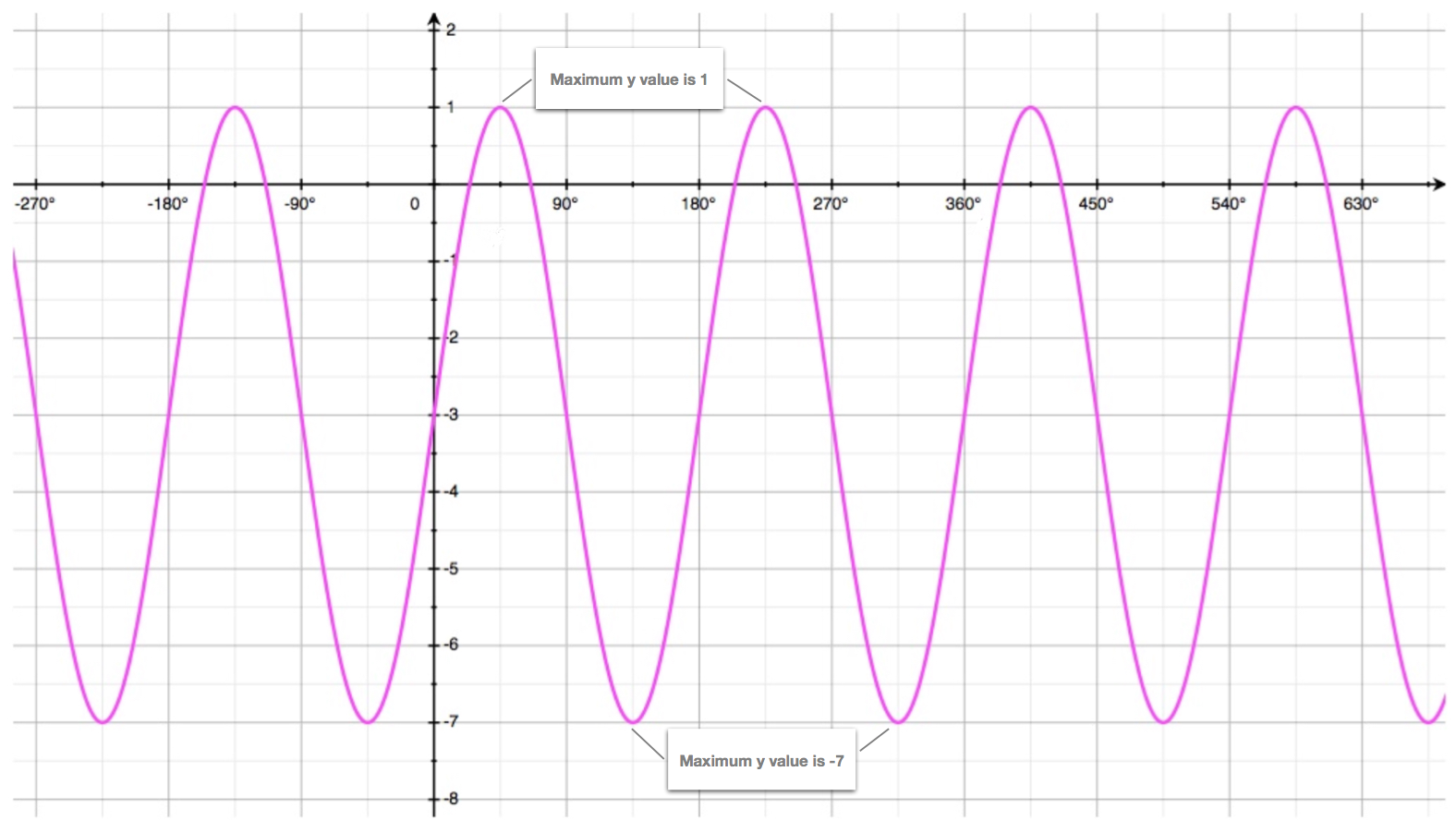
Given the graph of a cosine, or sine, curve we can find the value of its amplitude using the formula: \[a = \frac{y_{\text{max}} - y_{\text{min}}}{2}\] Where:
- \(y_{\text{min}}\) is the lowest point on the curve.
- \(y_{\text{max}}\) is the highest point on the curve.
The Wave Number: \(b\)
Given the graph of either a cosine or a sine function, the wave number \(b\), also known as angular frequency, tells us:
It is inversely proportional to the function's period \(T\). This means that the greater \(b\) is: the smaller the period becomes.
The wave number \(b\) is illustrated here, using the sine function defined by: \[y = 2.sin(3x)\]
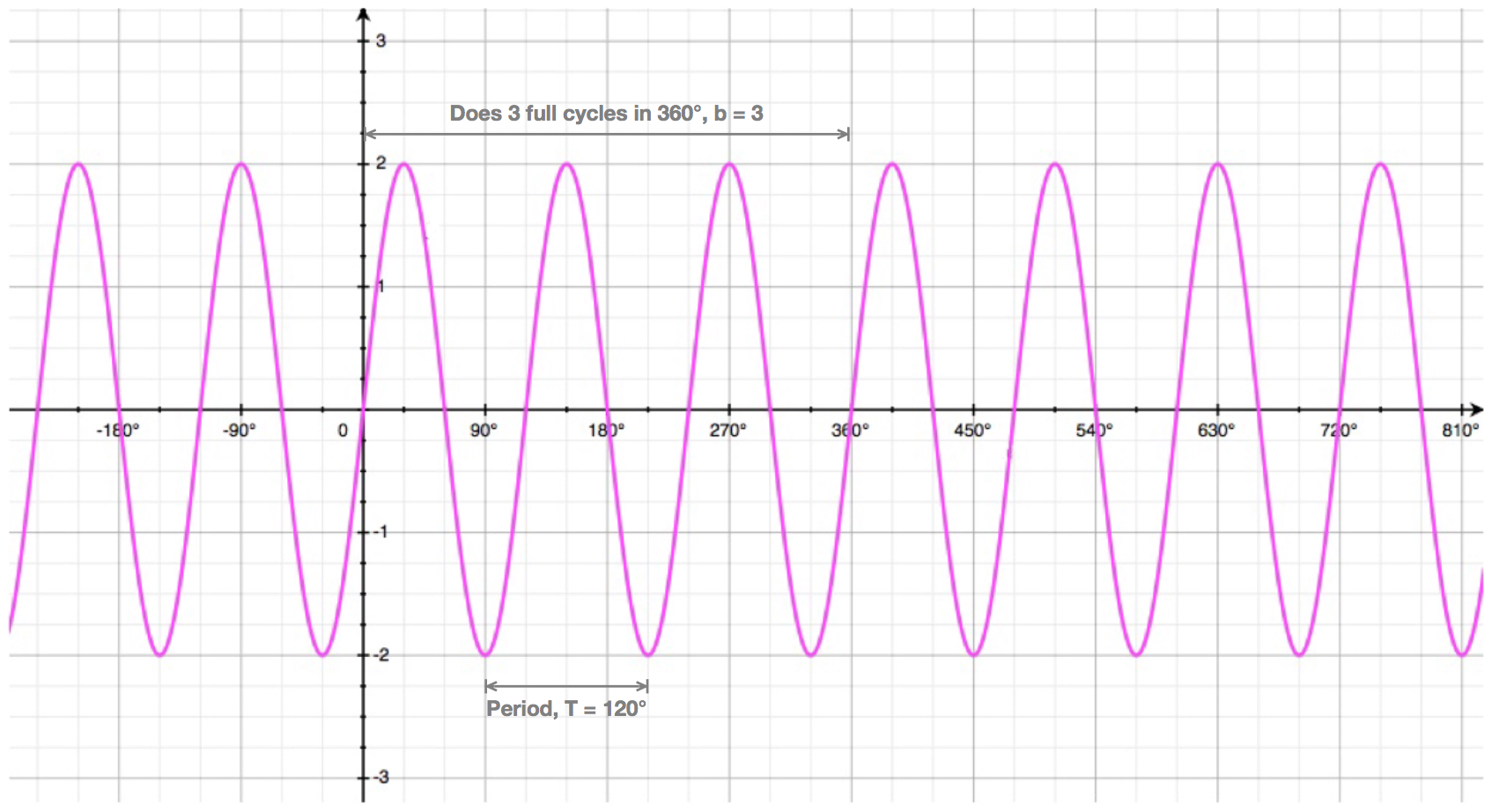
We can see from the equation \(y = 2.sin(3x)\) that the wave number is: \[b = 3\] On the graph, this can be seen from the fact that the curve completes \(3\) full cycles every \(360^{\circ}\).
We can also find the wave number if we know a cosine, or sine, curve's period \(T\). In that case, the wave number \(b\) can be found using the formula given below.
Formula: wave number \(b\)
Given a cosine, or sine, curve with period \(T\), its wave number \(b\) can be calculated using the formula: \[b = \frac{360}{T}\]
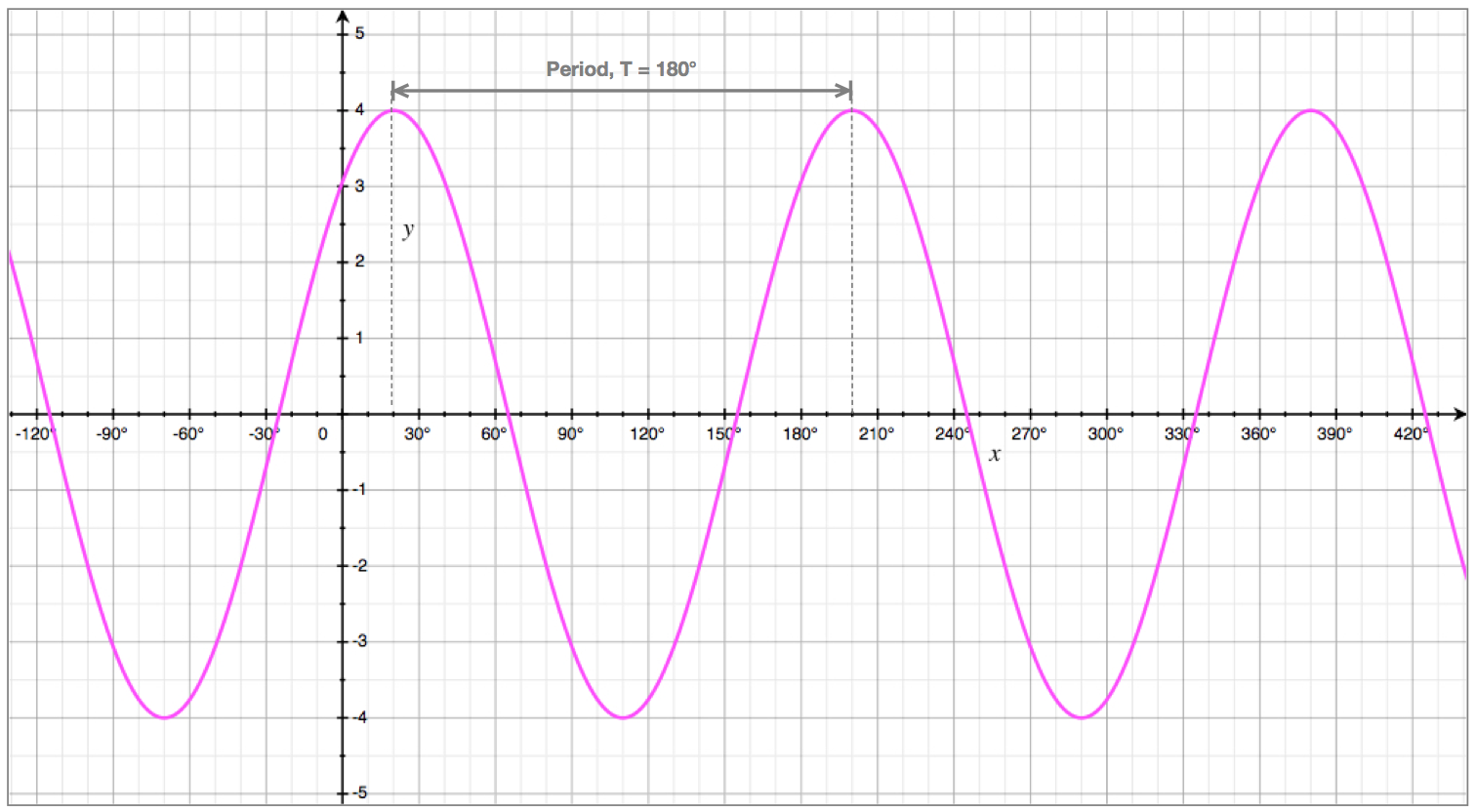
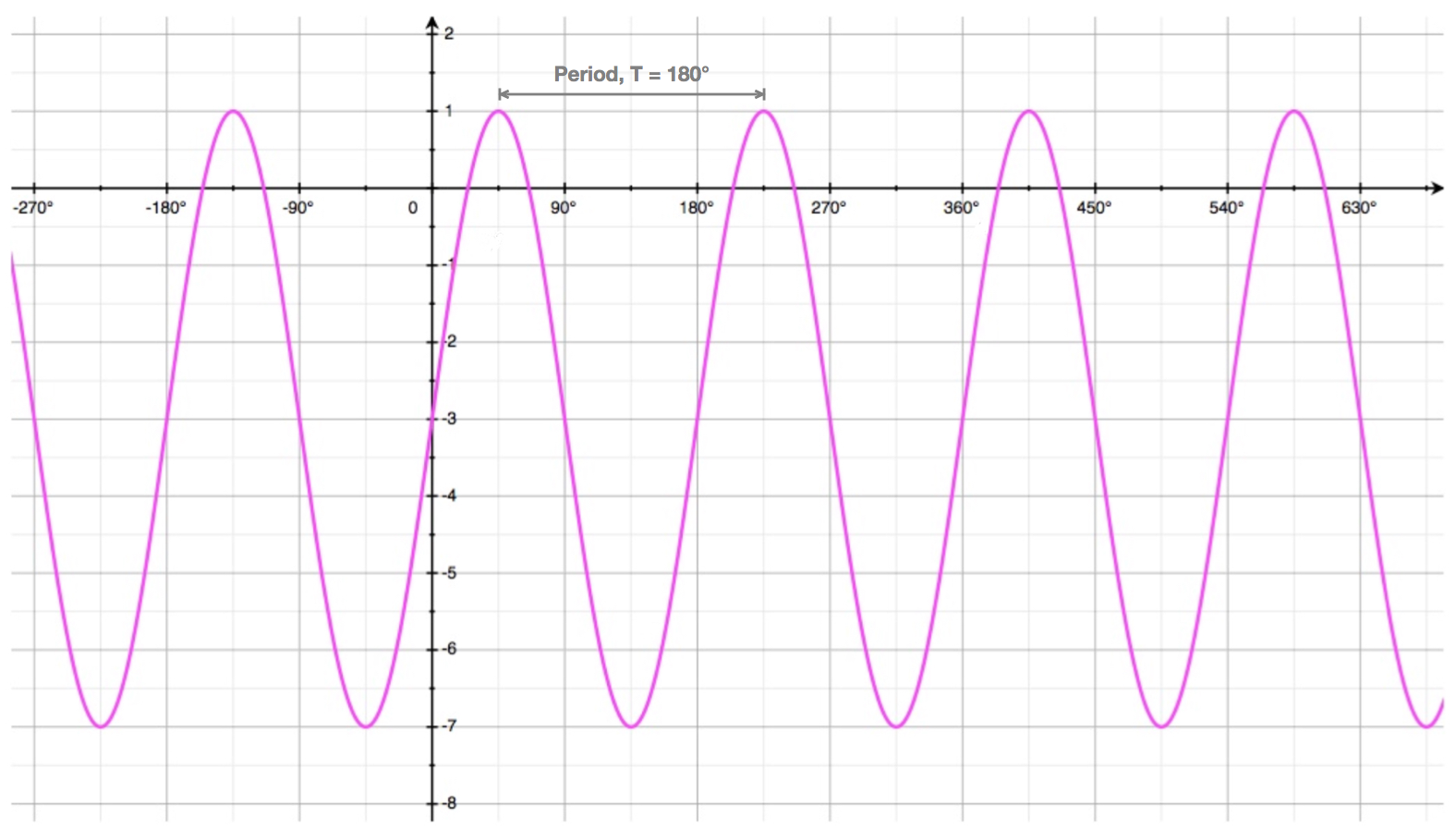
Example
Consider the cosine curve shown here:
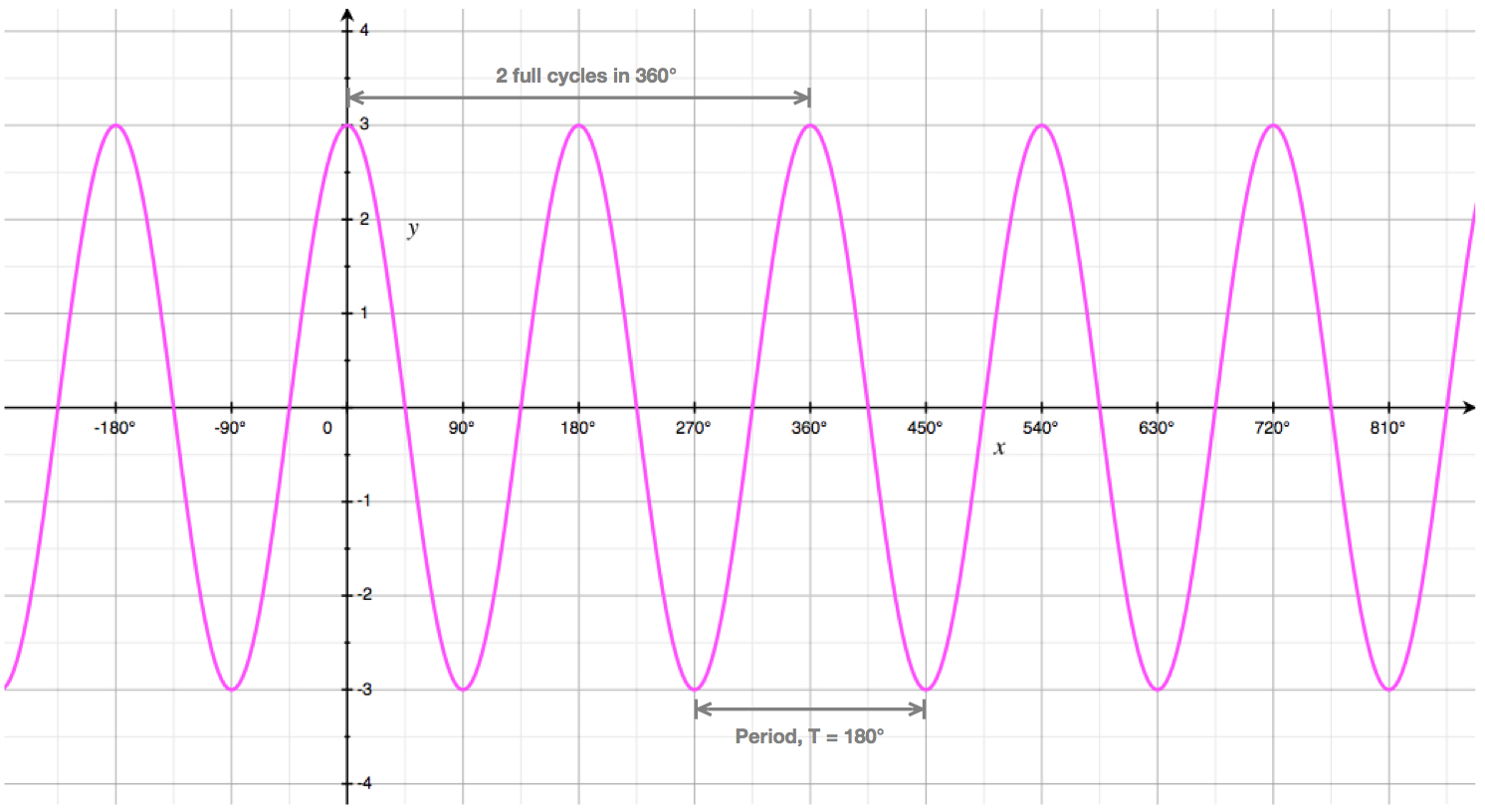
Given this curve has equation \(y = 3.cos(bx)\), find the value of \(b\).
Solution
We can see that:
- the curve completes \(2\) cycles every \(360^{\circ}\)
- it has a period \(T = 180^{\circ}\).
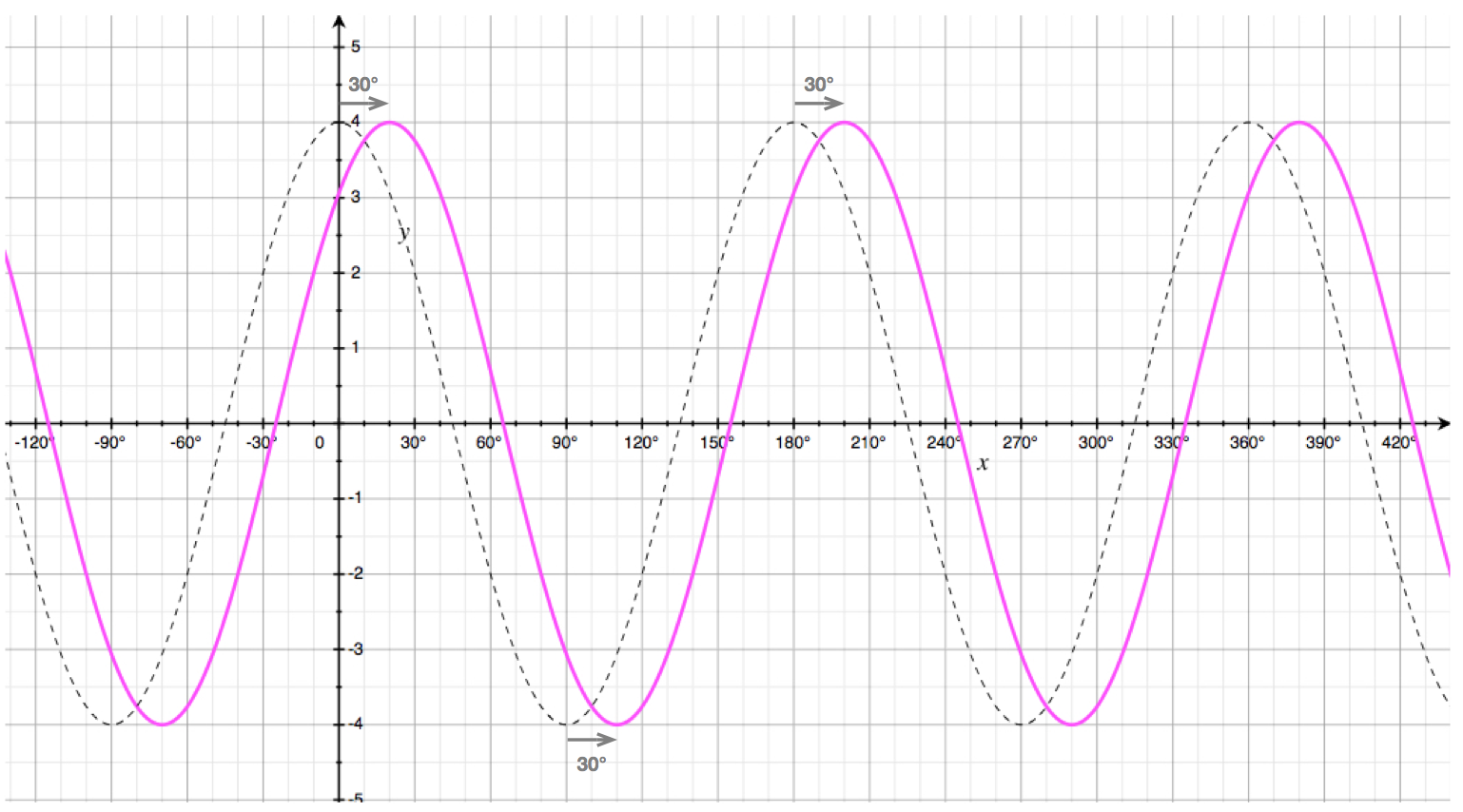
Finding the Phase Shift: \(c\)
The phase shift correponds to a horizontal translation of the cosine, or sine, curve.
Graphically, it can be seen by looking at how far to the right (or to the left) the curve without \(c\) has been moved.
For example, the following graph shows the curve: \[y = 3.sin\begin{pmatrix}x - 30 \end{pmatrix}\] as well as the curve \(y = 3.sin(x)\) in dotted gray lines.
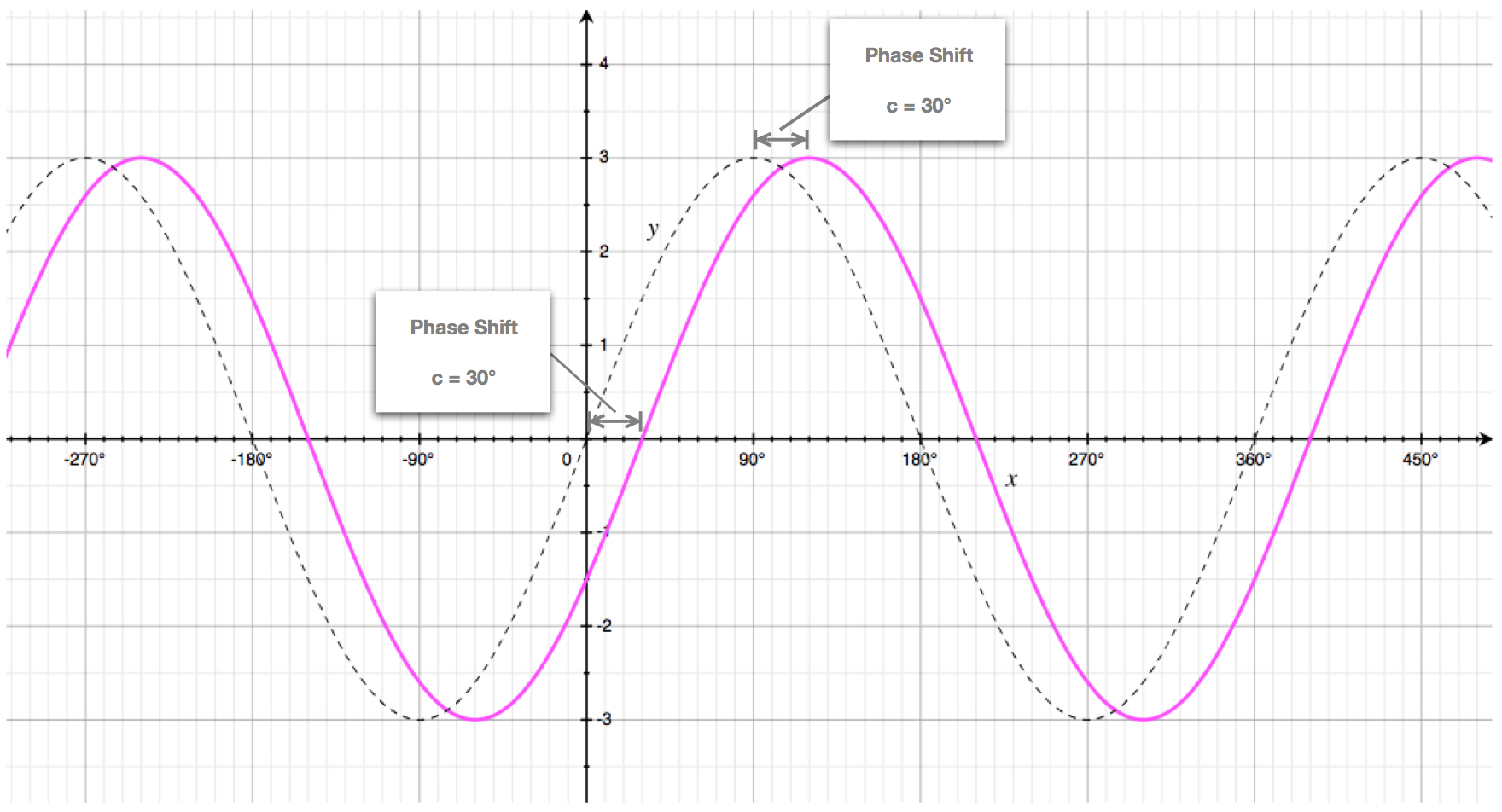
We can see that the phase shift of \(30^{\circ}\) moves the entire curve \(y=3.sin(x)\) \(30^{\circ}\) to the right.
Method
For a cosine curve, \(y = a.cos\begin{pmatrix}b(x-c)\end{pmatrix} + d\), or a sine curve, \(y = a.sin\begin{pmatrix}b(x-c)\end{pmatrix} + d\), we can find the phase shift \(c\) directly from its curve as follows:
- For a cosine curve \(y = a.cos\begin{pmatrix}b(x-c)\end{pmatrix} + d\)
Example
The following curve has equation \(y = a.cos\begin{pmatrix}b(x - c) \end{pmatrix}\).
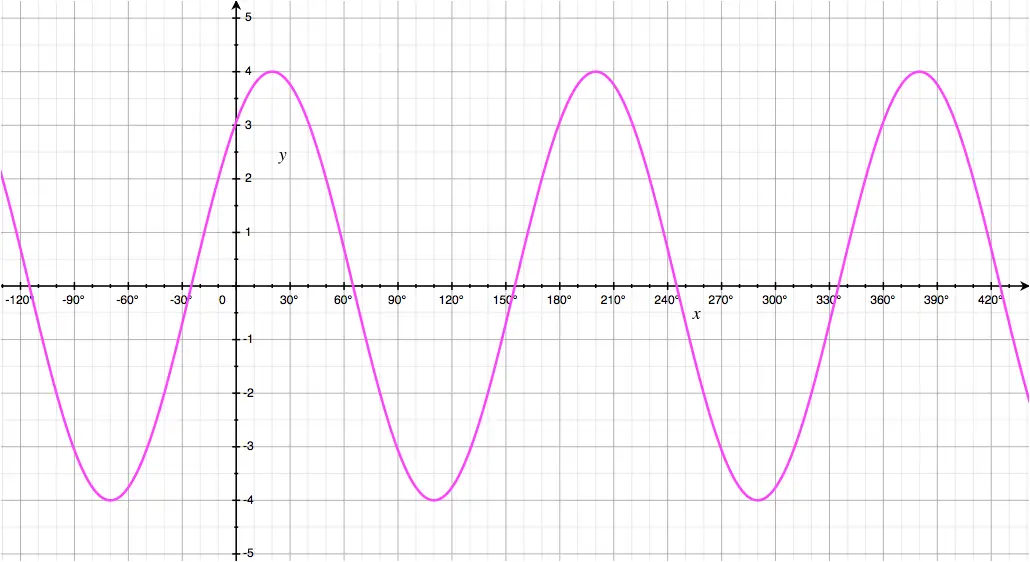
- Find:
- The value of the amplitude \(a\).
- The value of the wave number \(b\).
- The value of the phase shift \(c\).
- Given that this curve's equation can be written in the form: \[y = a.cos\begin{pmatrix}bx+p\end{pmatrix}\] state the value of \(p\).
The Vertical Shift: \(d\)
(the "rest" position)
Given the graph of either a cosine or a sine function, to find the rest position \(d\), which is the amount the curve has been translated vertically, we can use the following formula.
This is illustrated here:
- the pink curve shows \(y = 3.sin(x)+2\)
- the dotted curve shows \(y = 3.sin(x)\)
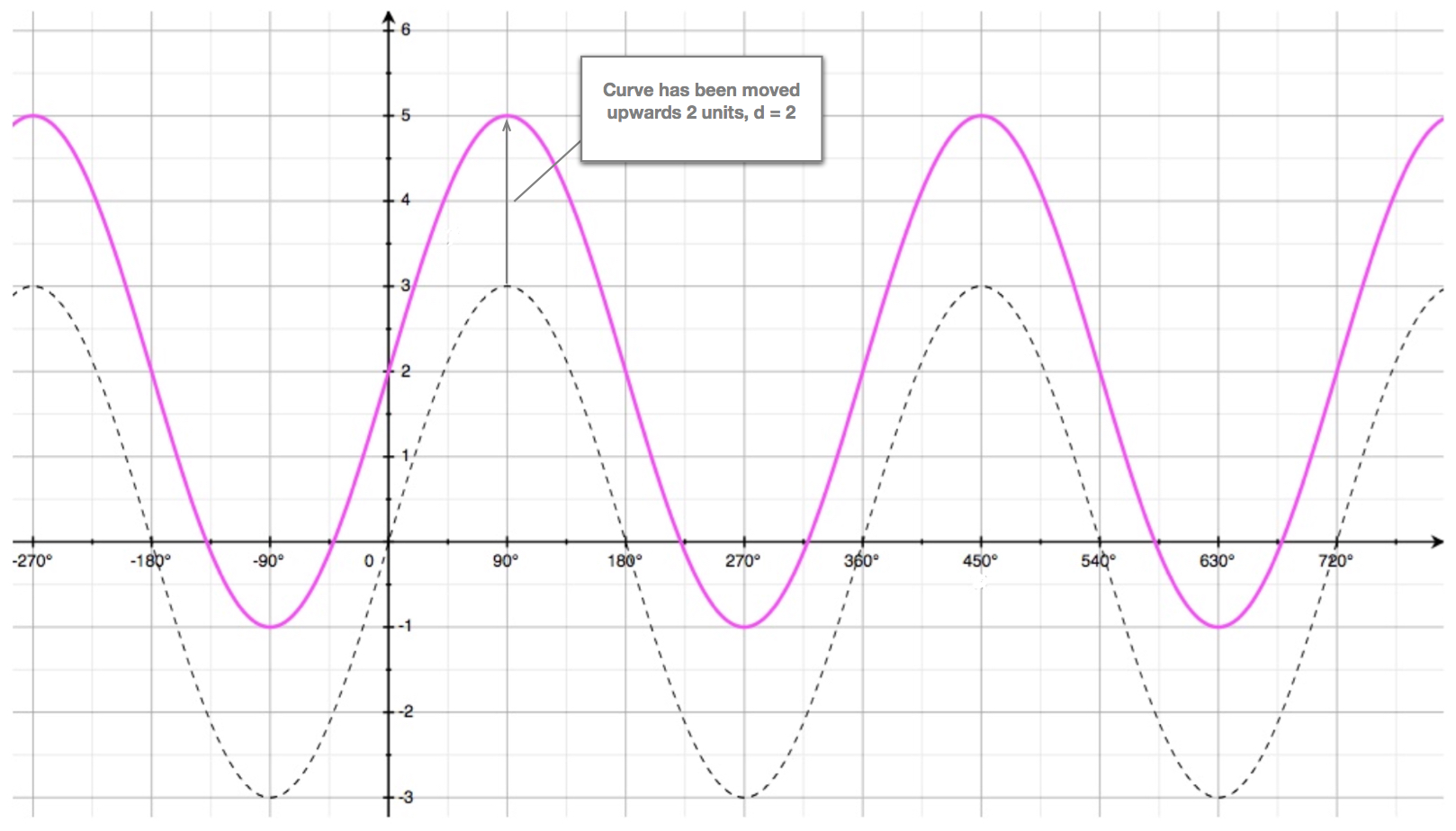
We can see that the pink curve, \(y=3.sin(x)+2\) is the same as the dotted curve but it has been moved \(2\) units upwards.
The pink curve \(y=3.sin(x)+2\) oscillated above and below the "new" rest poistion \(y=2\).
If we can't see/read the value of the vertical shift directly off the graph, we can use the following formula to find the value of \(d\).
Formula: vertical translation \(d\)
\[d = \frac{y_{\text{max}} + y_{\text{min}}}{2}\] Where:
- \(y_{\text{min}}\) is the lowest point on the curve.
- \(y_{\text{max}}\) is the highest point on the curve.
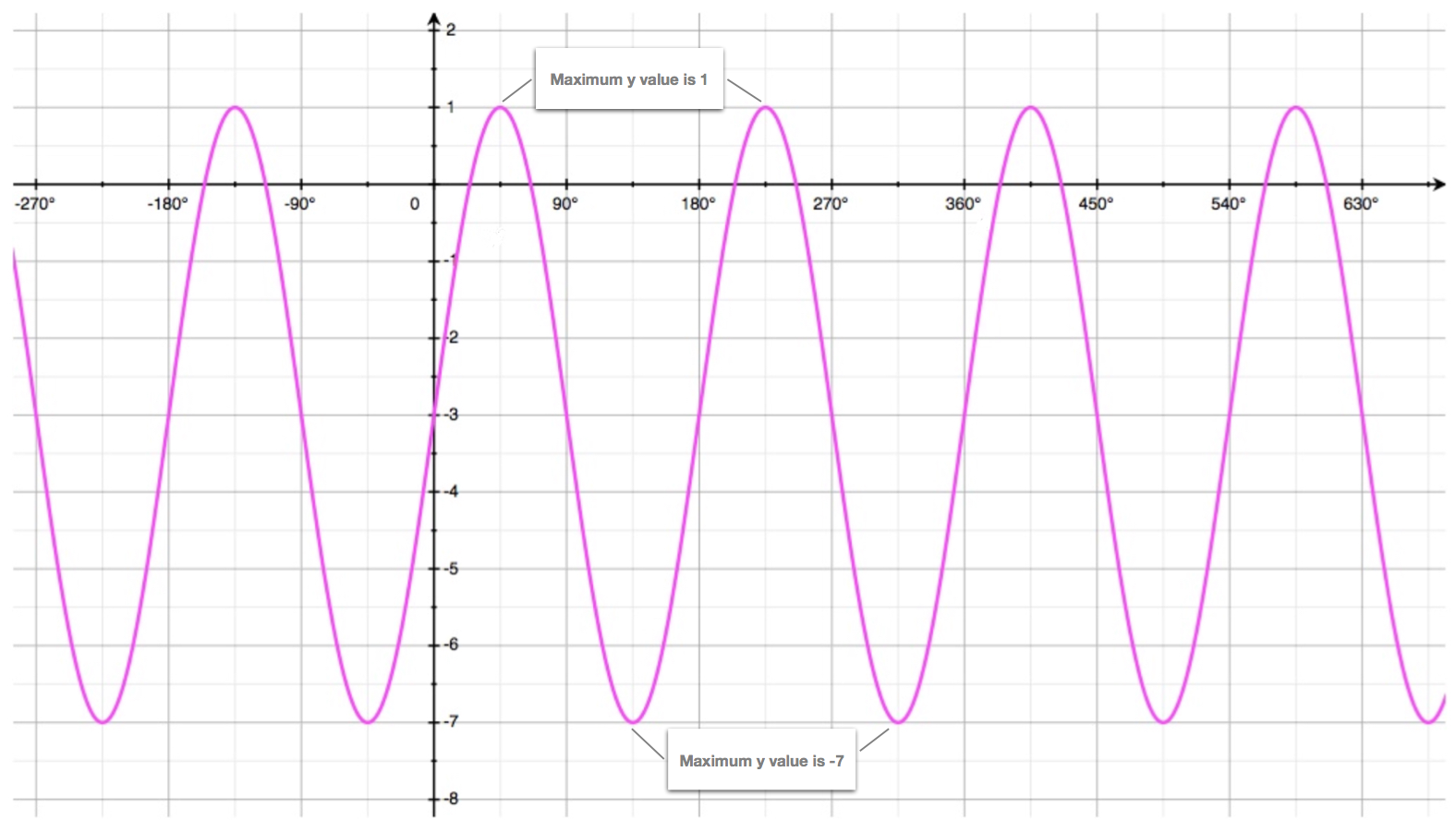
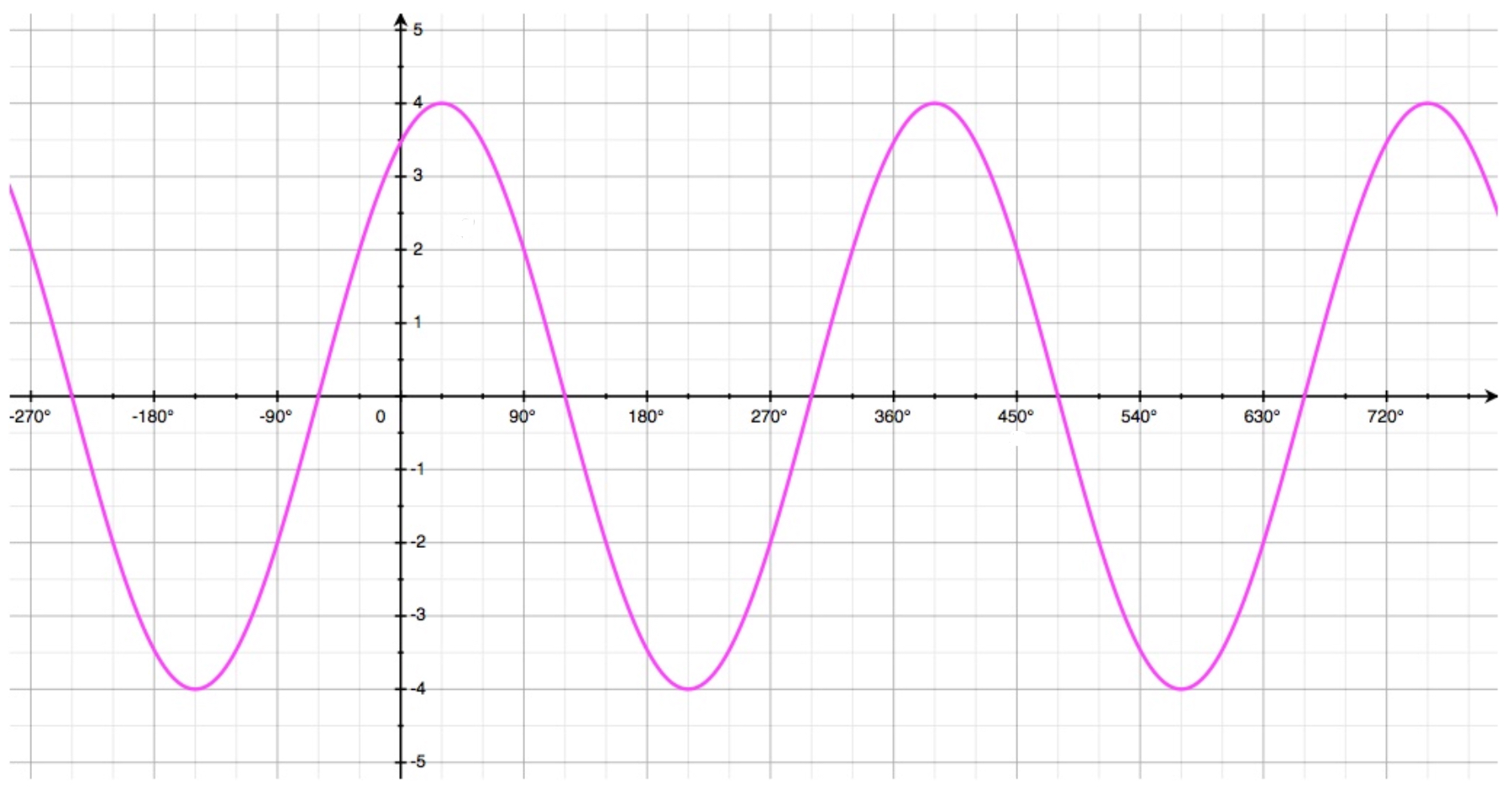
Example
The curve shown here has equation: \[y = a.sin(bx)+d\]
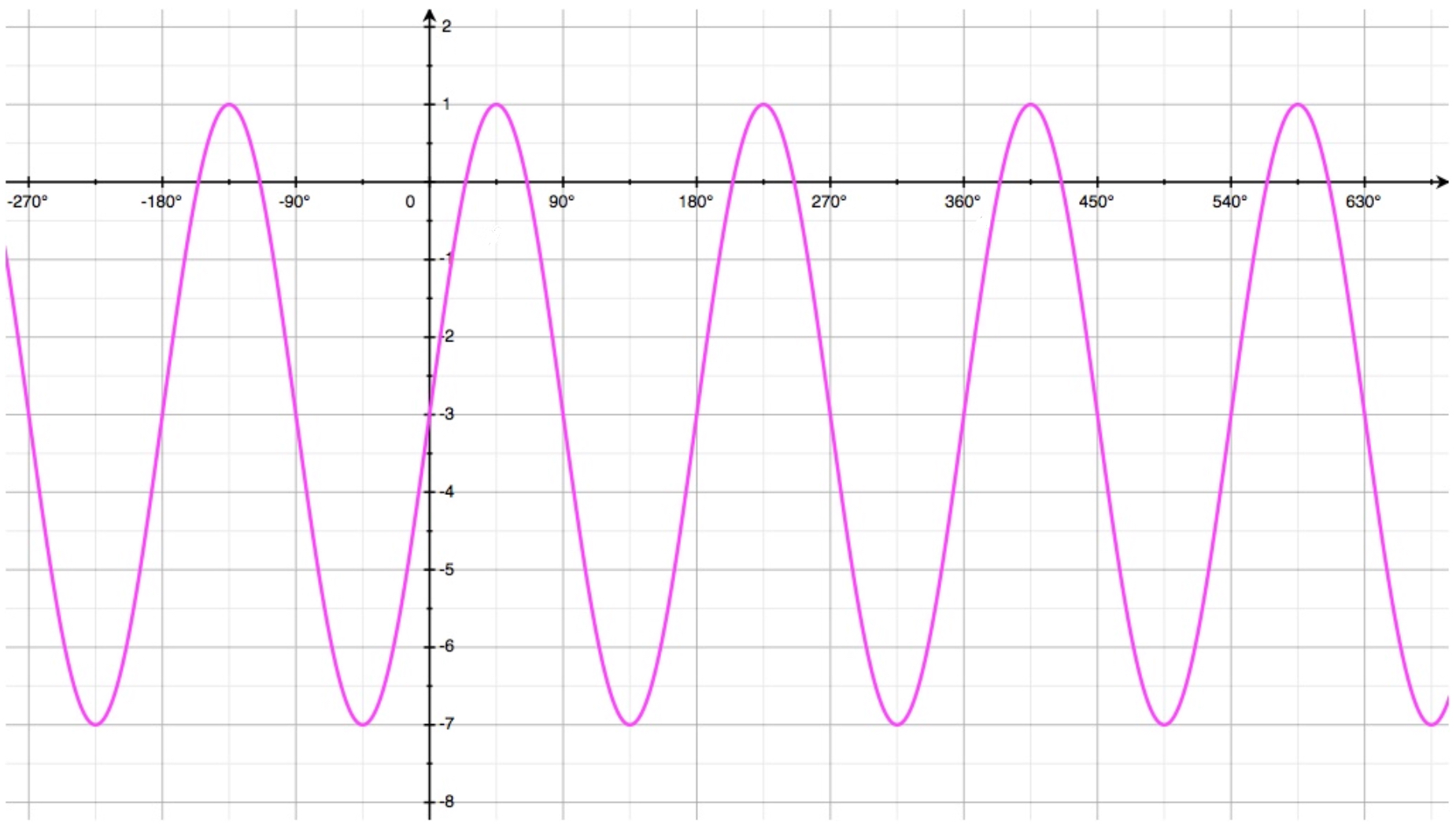
- Find the value of \(a\).
- Find the value of \(b\).
- Find the value of \(d\).
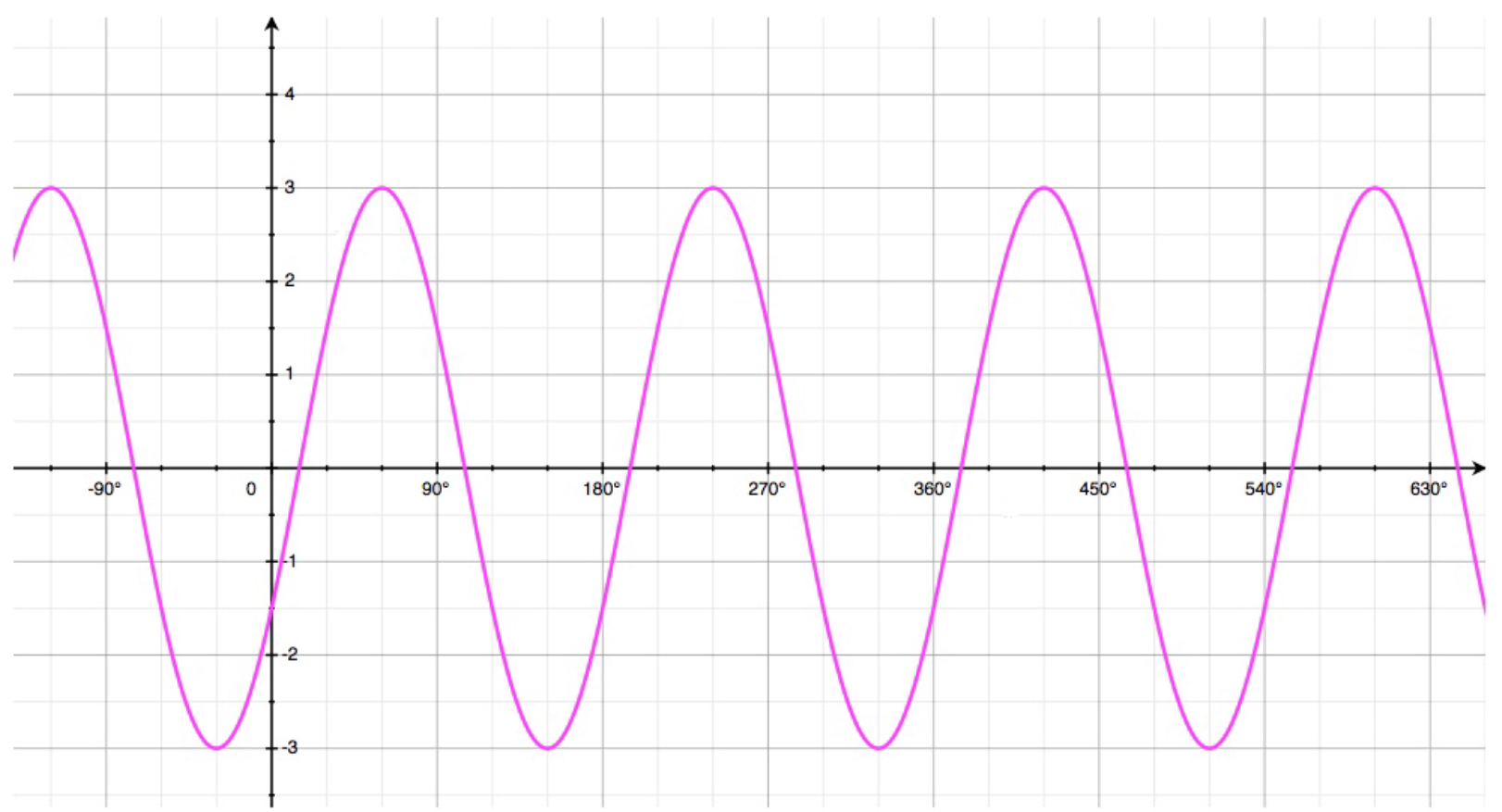
Exercise 1
The curve, shown below, has equation: \[y = a.sin(bx)\]
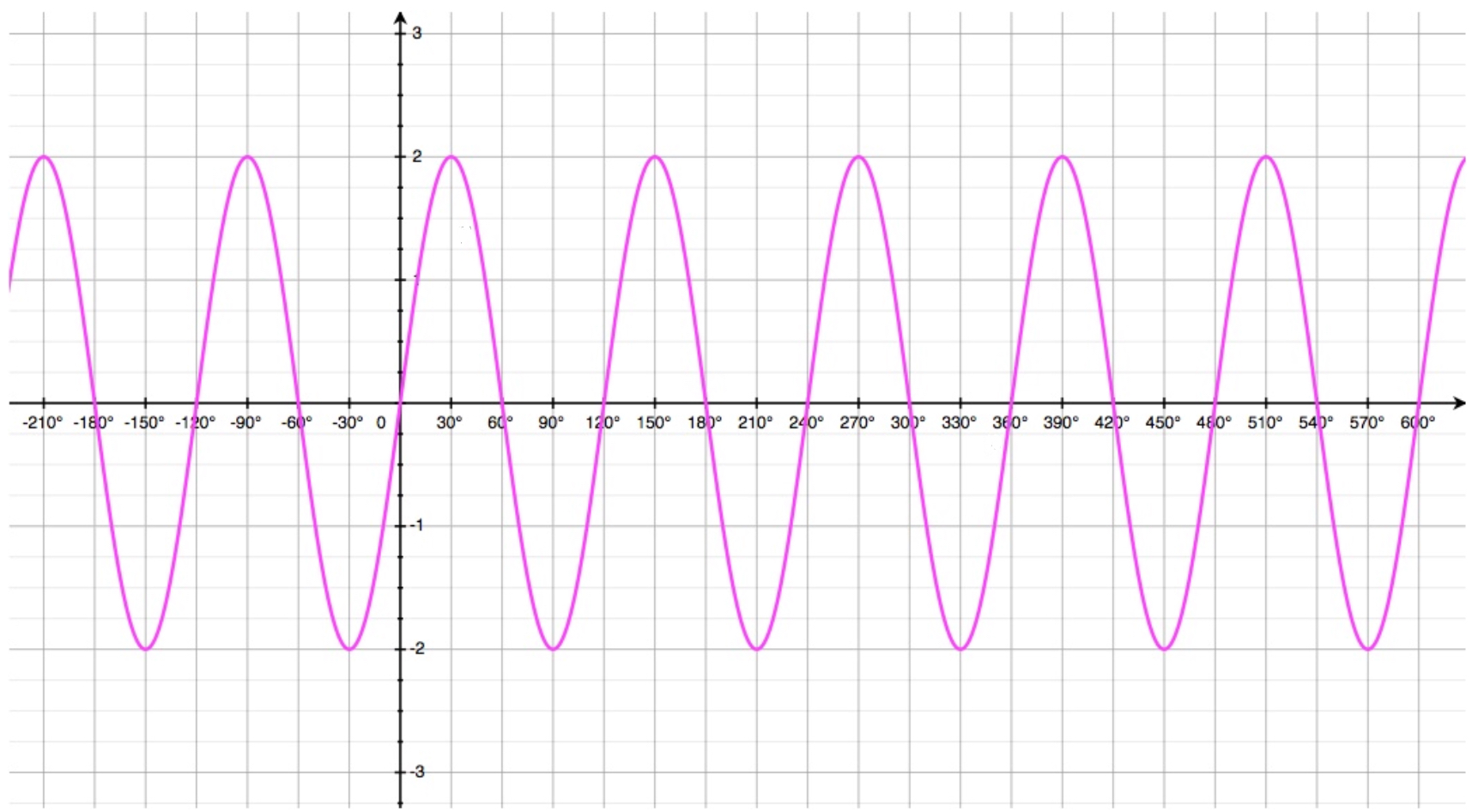
- Find the value of \(a\).
- Find the value of \(b\).
Answers Without Working
- The amplitude is \(a = 2\).
- The wave number is \(b=3\).