RadfordMathematics.com

Vertex Form of a Parabola

(finding the equation of a parabola)

We learn how to find the equation of a parabola by writing it in vertex form

In the previous section, we learnt how to write a parabola in its vertex form and saw that a parabola's equation: \[y = ax^2+bx+c\] could be re-written in vertex form: \[y = a\begin{pmatrix}x - h \end{pmatrix}^2+k\] where:

  • \(h\): is the horizontal coordinate of the vertex
  • \(k\): is the vertical coordinate of the vertex.
This is illustrated here:

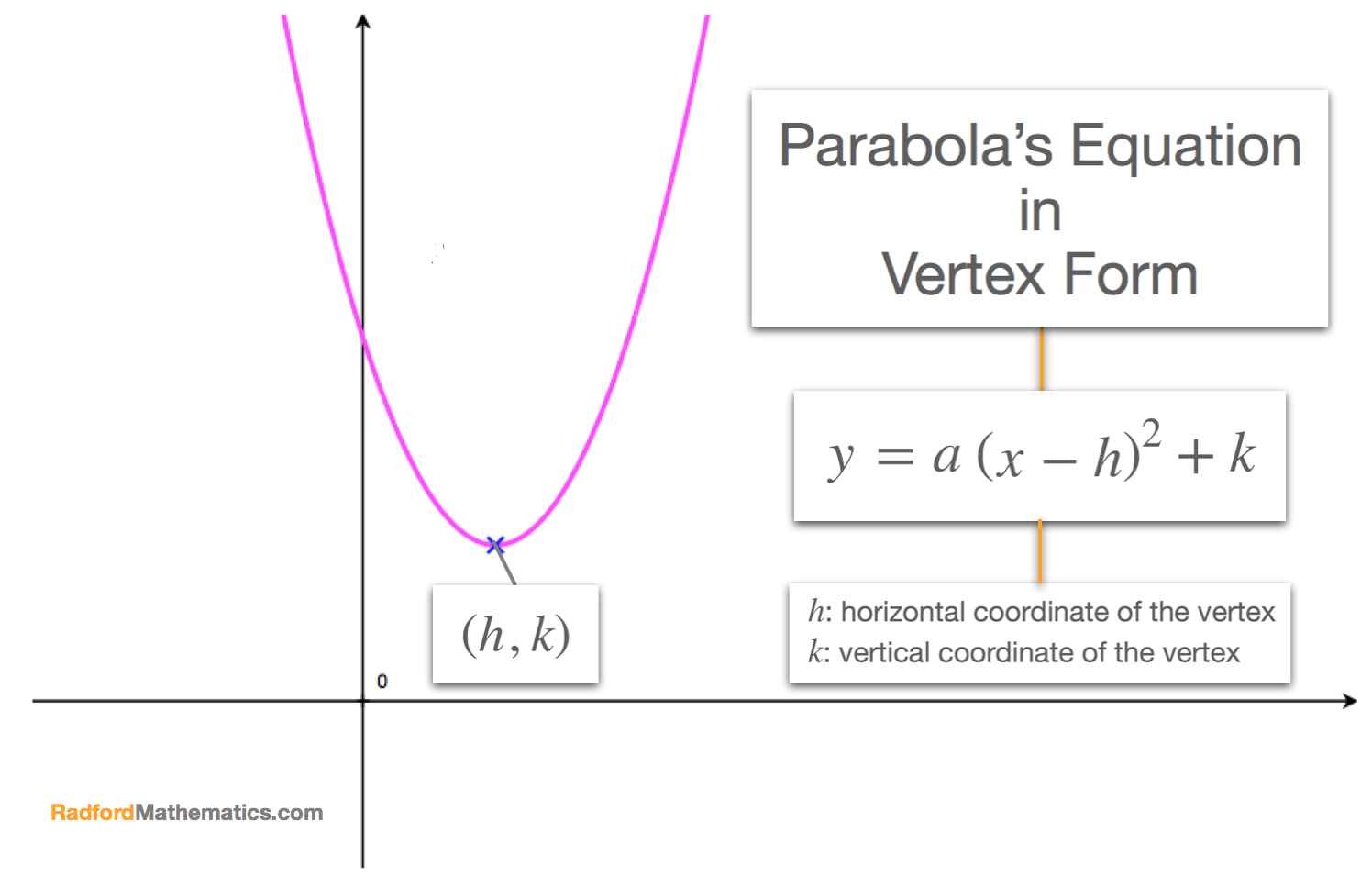
We can use the vertex form to find a parabola's equation. The idea is to use the coordinates of its vertex (maximum point, or minimum point) to write its equation in the form \(y=a\begin{pmatrix}x-h\end{pmatrix}^2+k\) (assuming we can read the coordinates \(\begin{pmatrix}h,k\end{pmatrix}\) from the graph) and then to find the value of the coefficient \(a\).

This is explained in the step-by-stem mathod, below, as well as in the tutorials.

How to find a parabola's equation using its Vertex Form

Given the graph of a parabola for which we're given, or can clearly see:

  • the coordinates of the vertex, \(\begin{pmatrix}h,k\end{pmatrix}\), and:
  • the coordinates another point \(P\) through which the parabola passes.
we can find the parabola's equation in vertex form following two steps:
  • Step 1: use the (known) coordinates of the vertex, \(\begin{pmatrix}h,k\end{pmatrix}\), to write the parabola's equation in the form: \[y = a\begin{pmatrix}x-h \end{pmatrix}^2+k\] the problem now only consists of having to find the value of the coefficient \(a\).
  • Step 2: find the value of the coefficient \(a\) by substituting the coordinates of point \(P\) into the equation written in step 1 and solving for \(a\).

This two-step method is better/further explained in the following tutorial, take the time to watch it now.

Tutorial 1

In the following tutorial we learn how to find a parabola's using the coordinates of its vertex as well as the coordinates of its \(y\)-intercept.

Exercise 1

Using the two-step method we've just learned, find the equation of each of the following parabola in the following two forms:

  1. \(y=a\begin{pmatrix}x-h\end{pmatrix}^2+k\)
  2. \(y = ax^2+bx+c\)

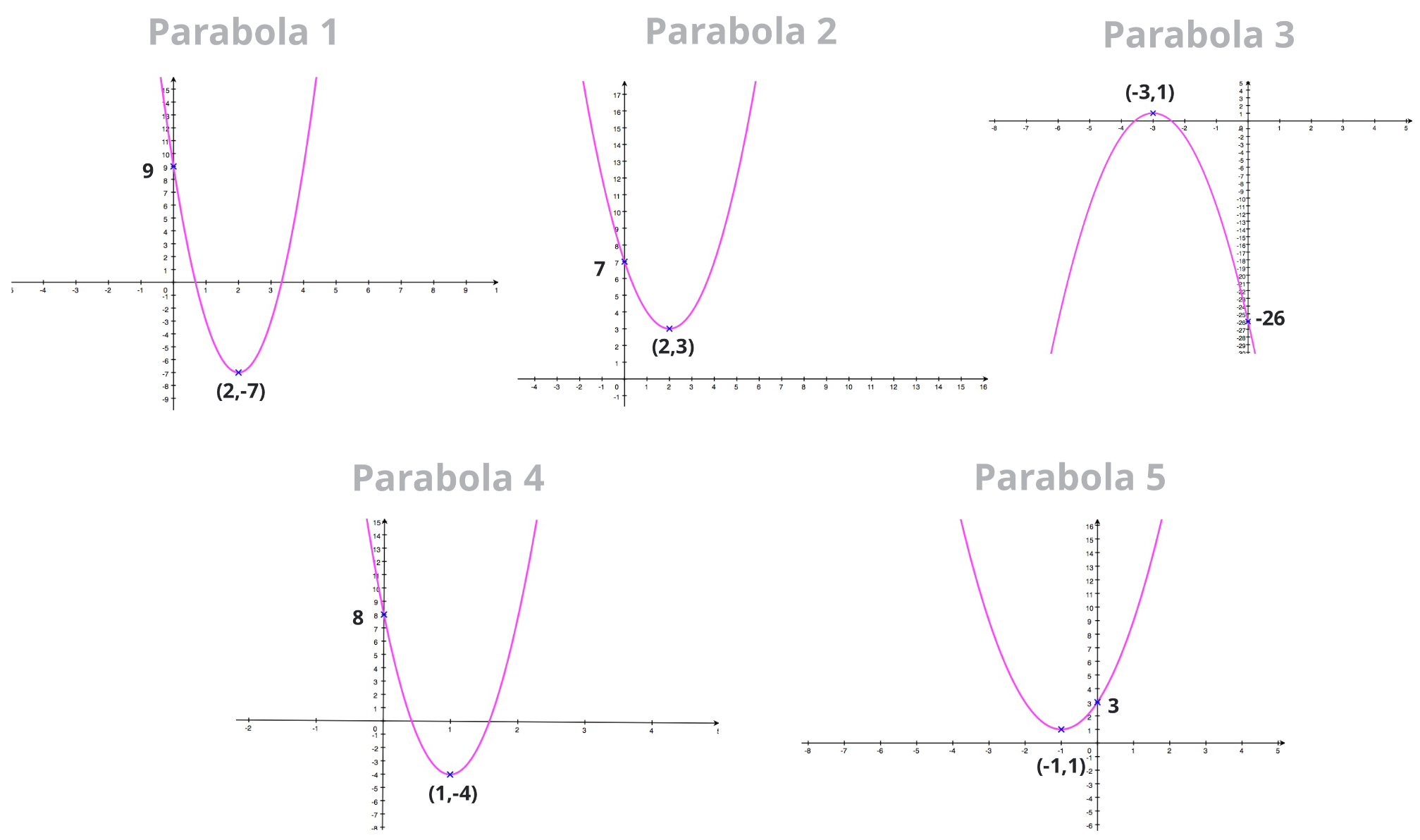
Note: this exercise can be downloaded as a worksheet to practice with worksheet

Answers Without Working

  • Parabola 1:
    1. \(y = 4 \begin{pmatrix}x-2\end{pmatrix}^2-7\)
    2. \(y = 4x^2 - 16x + 9\)
  • Parabola 2:
    1. \(y = \begin{pmatrix}x-2\end{pmatrix}^2+ 3\)
    2. \(y = x^2 - 4x +7\)
  • Parabola 3:
    1. \(y = -3 \begin{pmatrix}x+3 \end{pmatrix}^2+1\)
    2. \(y=-3x^2 - 18x - 26\)
  • Parabola 4:
    1. \(y = 12 \begin{pmatrix}x-1\end{pmatrix}^2-4\)
    2. \(y = 12x^2 - 24x + 8\)
  • Parabola 5:
    1. \(y = 2\begin{pmatrix}x+1 \end{pmatrix}^2+1\)
    2. \(y = 2x^2+4x+3\)

Tutorial 2

In the following tutorial we learn how to find a parabola's using the coordinates of its vertex as well as the coordinates of another point along its length (that isn't the \(y\)-intercept).

Exercise 2

For each of the parabola shown here:

  1. Find its equation in vertex form \(y=a\begin{pmatrix}x - h \end{pmatrix}^2+k\)
  2. Find its equation in standard form \(y=ax^2+bx+c\)

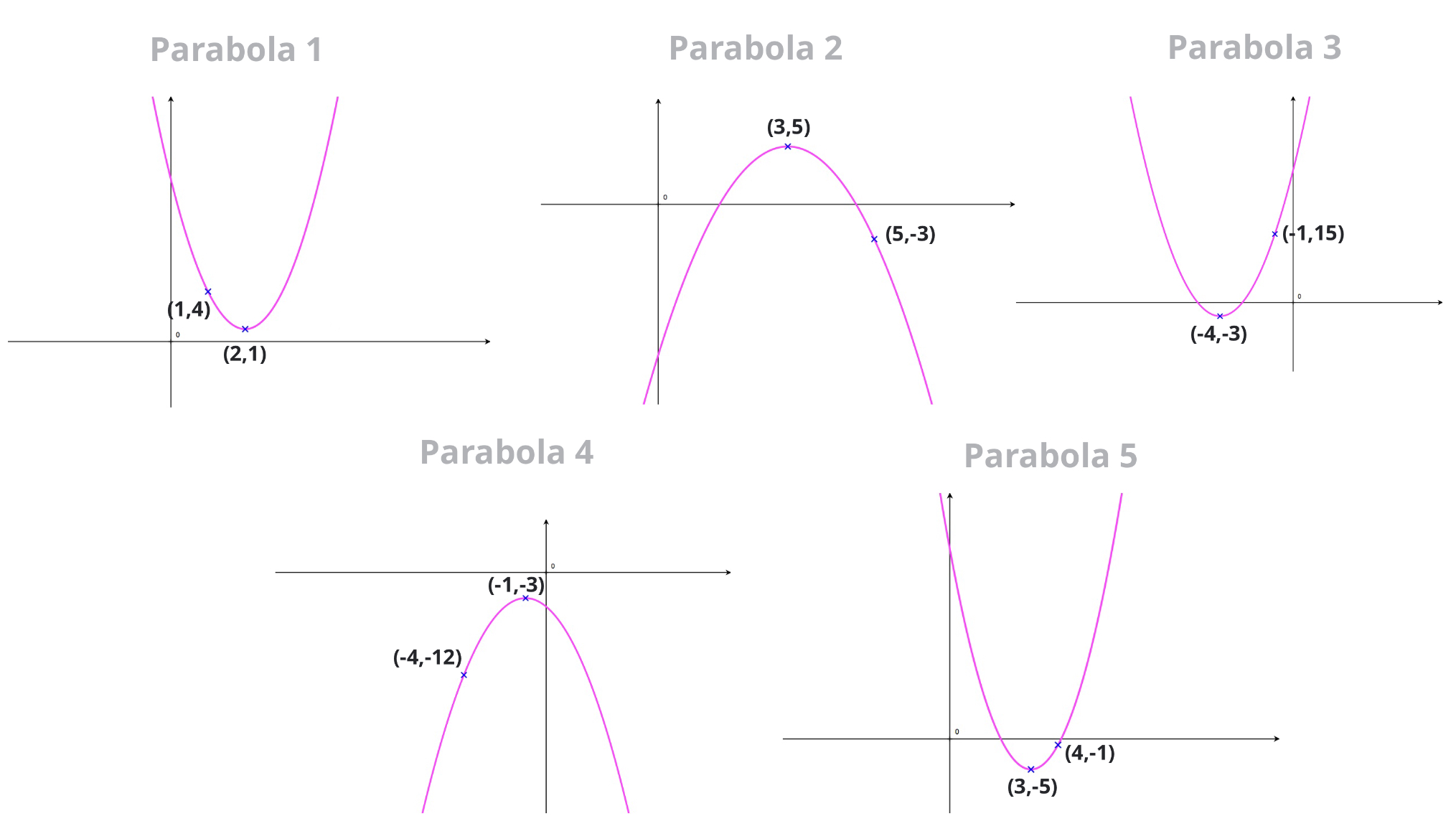
Note: this exercise can be downloaded as a worksheet to practice with: worksheet

Answers Without Working

  • Parabola 1:
    1. \(y = 3 \begin{pmatrix}x-2\end{pmatrix}^2+1\)
    2. \(y = 3x^2 - 12x + 13\)
  • Parabola 2:
    1. \(y = -2\begin{pmatrix}x-3\end{pmatrix}^2+ 5\)
    2. \(y = -2x^2+12x-13\)
  • Parabola 3:
    1. \(y = 2 \begin{pmatrix}x+4 \end{pmatrix}^2-3\)
    2. \(y=2x^2+16x + 29\)
  • Parabola 4:
    1. \(y = - \begin{pmatrix}x+1\end{pmatrix}^2-3\)
    2. \(y = -x^2-2x-4\)
  • Parabola 5:
    1. \(y = 4\begin{pmatrix}x-3 \end{pmatrix}^2-5\)
    2. \(y = 4x^2 - 24x + 31\)