RadfordMathematics.com

Area of a Triangle Sine Formula

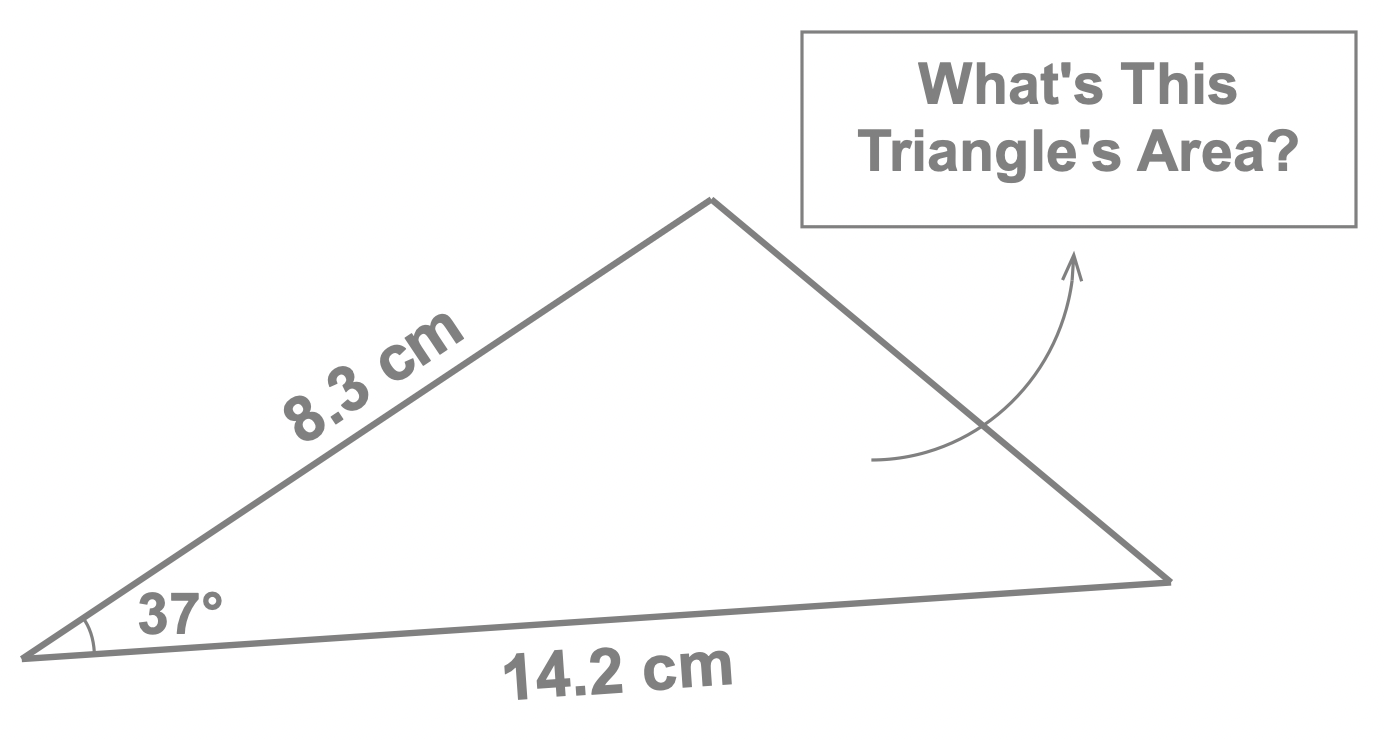Here we learn how to calculate the area of a triangle using sine. As we're about to learn: all we need to calculate the area of any triangle is:

  • two of its side lengths
  • the angle in between them
provided we have that amount of information we'll be able to use the formula we learn about here.

What we'll Find Here

  • Video tutorial: formula and worked example for calculating the area of a triangle with the sine formula
  • Sine Formula for the area of a triangle
  • explanation of the formula
  • Worked Examples 1 & 2

Area of a Triangle - Sine Formula

In the following tutorial we learn the Area of a Triangle with Sine Formula and work through an Example to see how to use it.

Formula : Area of a Triangle

Given a triangle, we can calculate its area provided we know 2 of its side lengths as well as the angle in between them.

We can do so with the following formula:

Explanation

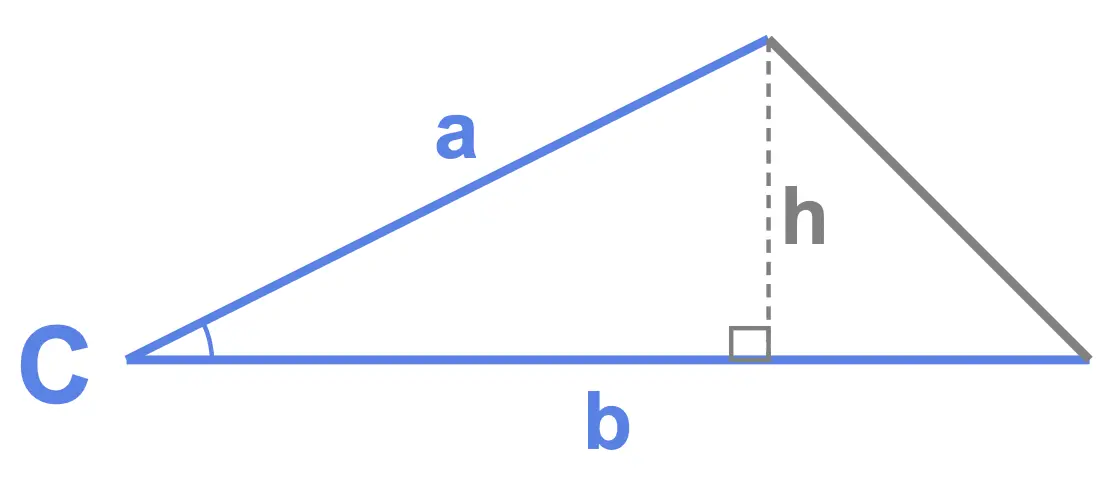
We already know that the area of a triangle is given by: \[\text{Area} = \frac{1}{2}\times \text{Base} \times \text{Height}\] Now consider the generic triangle in which side lengths \(a\) and \(b\) are known as well as the angle \(C\) between them. Its height, \(h\), is shown here:

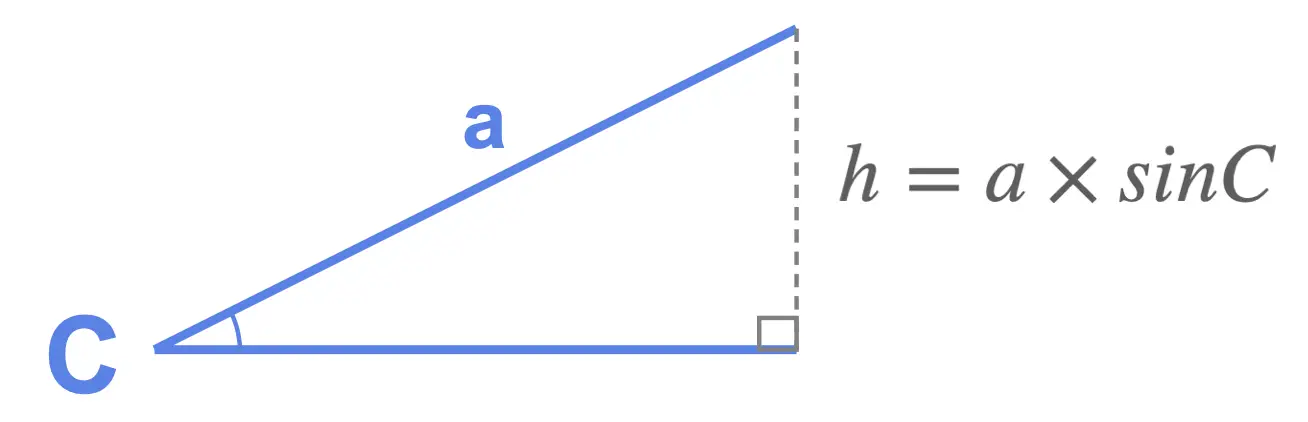
Again, this triangle's area is: \[\text{Area} = \frac{1}{2}\times \text{Base} \times \text{Height}\] Which is: \[\text{Area} = \frac{1}{2}\times b \times h\] Now, using the height \(h\), the side \(a\), the angle \(C\) and part of the base : we can construct the right angle triangle shown:
Since this is a right-angled triangle, we can use our knowledge of trigonometric ratios to state that: \[sinC = \frac{h}{a}\] Rearranging this to make \(h\) the subject: \[h= a\times sinC\]

Replacing \(h\) by \(a\times sinC\) in our formula \(\text{Area} = \frac{1}{2}\times b \times h\) we obtain: \[\text{Area} = \frac{1}{2} \times b \times a \times sinC\] Which we can write as our formula: \[\text{Area} = \frac{1}{2} . a . b . sinC\]

Example 1

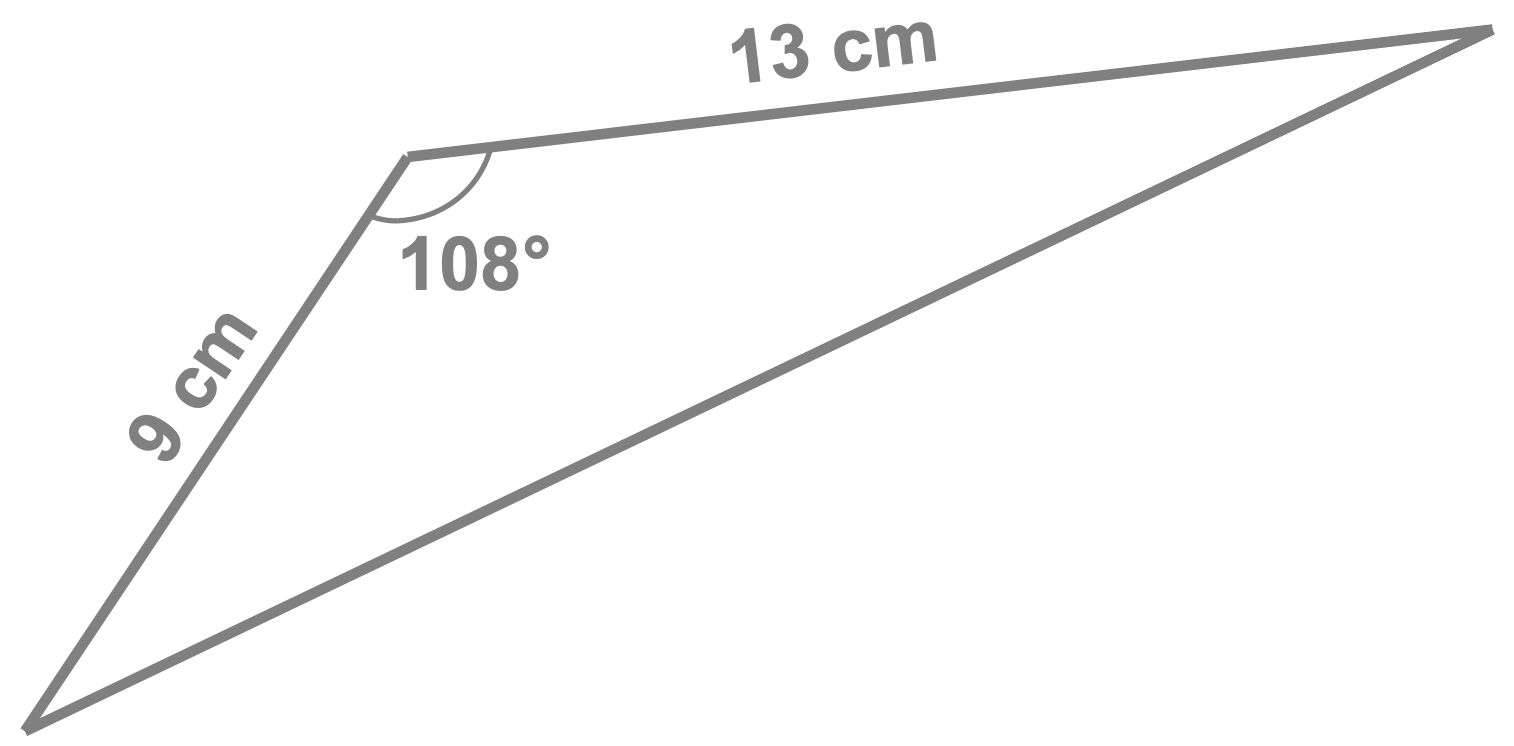Rounding your answer to 3 significant figures, calculate the area of the triangle shown here.

Solution

Looking at the information we have, we have two side lengths and the angle between them. Indeed we have:

  • two sides of lengths 9 cm and 13cm
  • the angle between them \(108^{\circ}\).

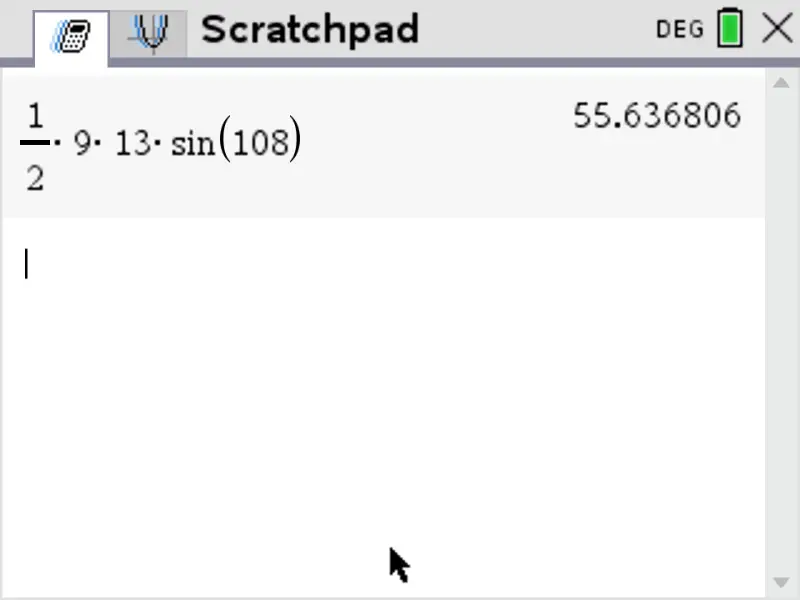We can therefore use our formula: \[\begin{aligned} \text{Area} & = \frac{1}{2} \times 9 \times 13 \times sin\begin{pmatrix}108 \end{pmatrix} \\ & = 55.636806 \\ \text{Area} &= 55.6\ \text{cm}^2 \quad \text{(rounded to 3 significant figures)} \end{aligned}\]

Example 2

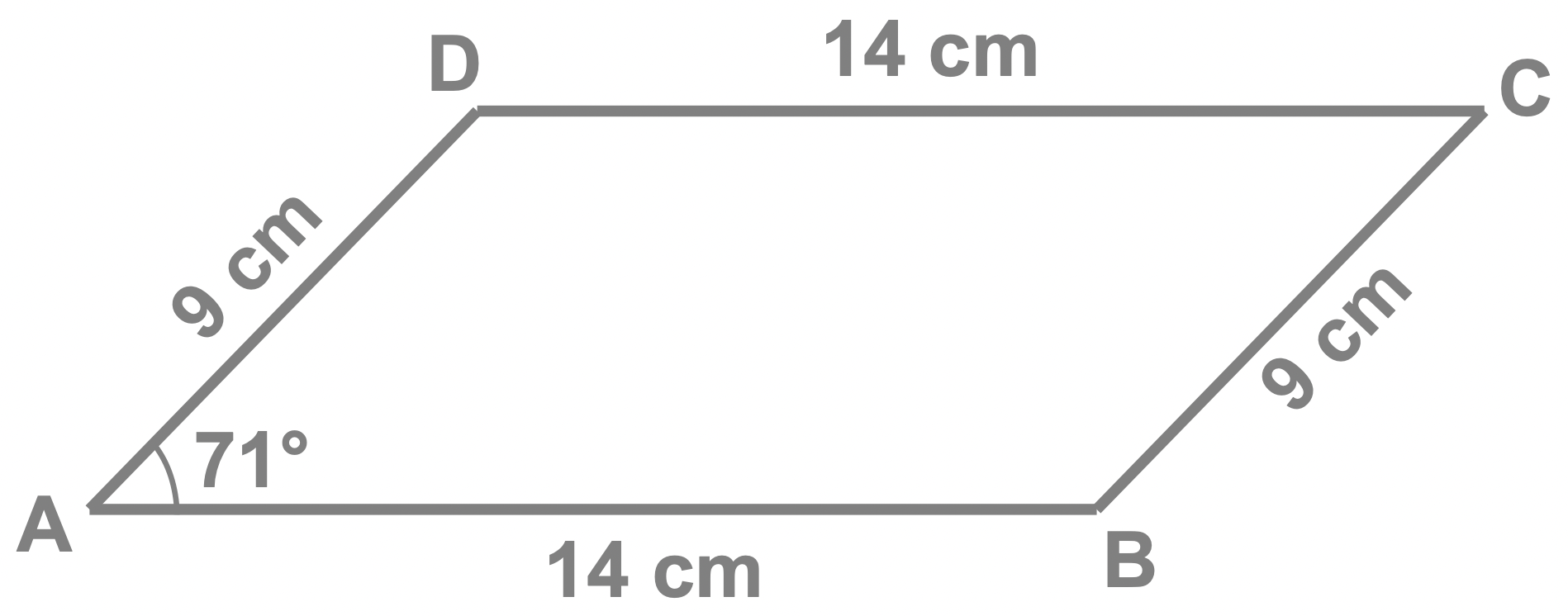Rounding your answer to 3 significant figures, calculate the area of the parallelogram ABCD.

Solution

The trick for calculating this parallelogram's area is to see that it can be thought of as two idetical triangles stuck together, one of which is illustrated here:

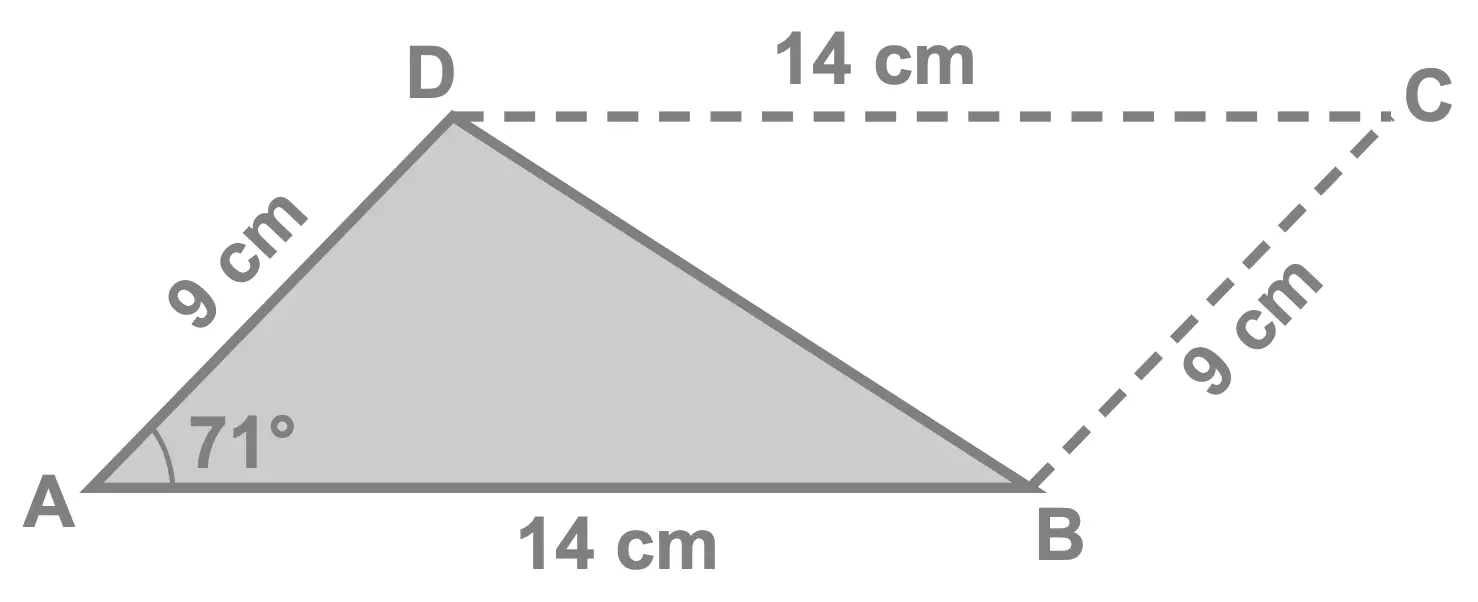
Consequently, to calculate the parallelogram's area we can calculate the area of the triangle \(ABD\) and multiply the result by 2.

So, using the formula for the area of a triangle with:

  • triangle's side lengths : 9 cm and 14 cm
  • angle between the sides : \(71^{\circ}\)
we can write: \[\begin{aligned} \text{Area of Triangle} & = \frac{1}{2} \times 9 \times 14 \times sin \begin{pmatrix}71 \end{pmatrix} \\ & = 59.56767\\ \end{aligned}\] So the triangle's area is \(59.56767 \ \text{cm}^2\).

Finally to calculate the parallelogram's area we multiply that result by \(2\): \[\begin{aligned} \text{Area of Parallelogram} & = 2\times \begin{pmatrix} \text{Area of Triangle} \end{pmatrix} \\ & = 2\times \begin{pmatrix} \frac{1}{2} \times 9 \times 14 \times sin \begin{pmatrix}71 \end{pmatrix} \end{pmatrix}\\ & = 2\times 59.56767 \\ \text{Area of Parallelogram} & = 119.13534 \end{aligned}\] Finally, rounding the answer to 3 significant figures we obtain the answer: \[\text{Area of Parallelogram} = 119 \ \text{cm}^2 \quad \text{(3 significant figures)}\]


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.