Cosine Rule for Unknown Sides & Unknown Angles
The Cosine Rule can be used to find unknown sides as well as find unknown angles in triangles that aren't right-angled (it works for right-angled triangles as well).
For an Unknown Side Length
Given a triangle with an unknown side length, we can use the cosine rule to find it
Where the side lengths \(a\), \(b\) and \(c\) refer to those on the generic triangle shown here:
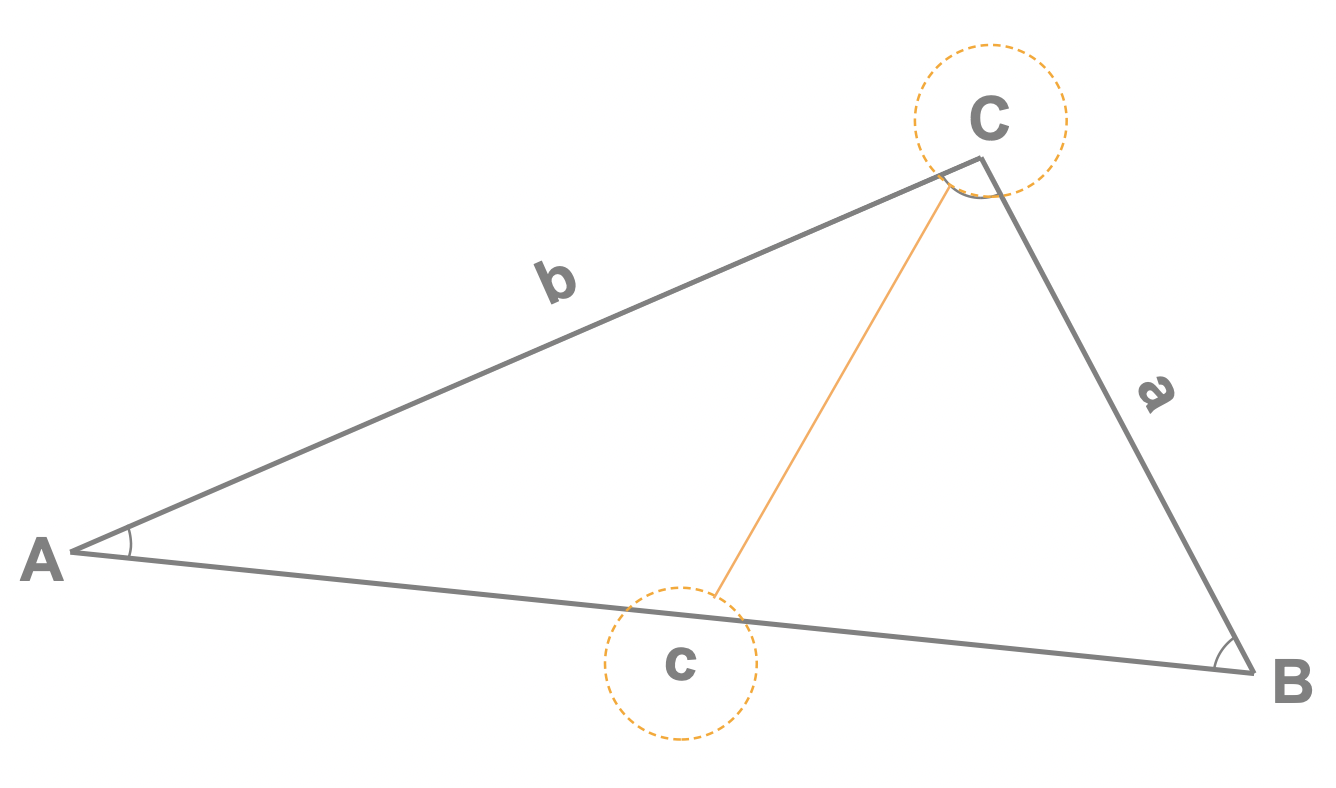
When to use the cosine rule
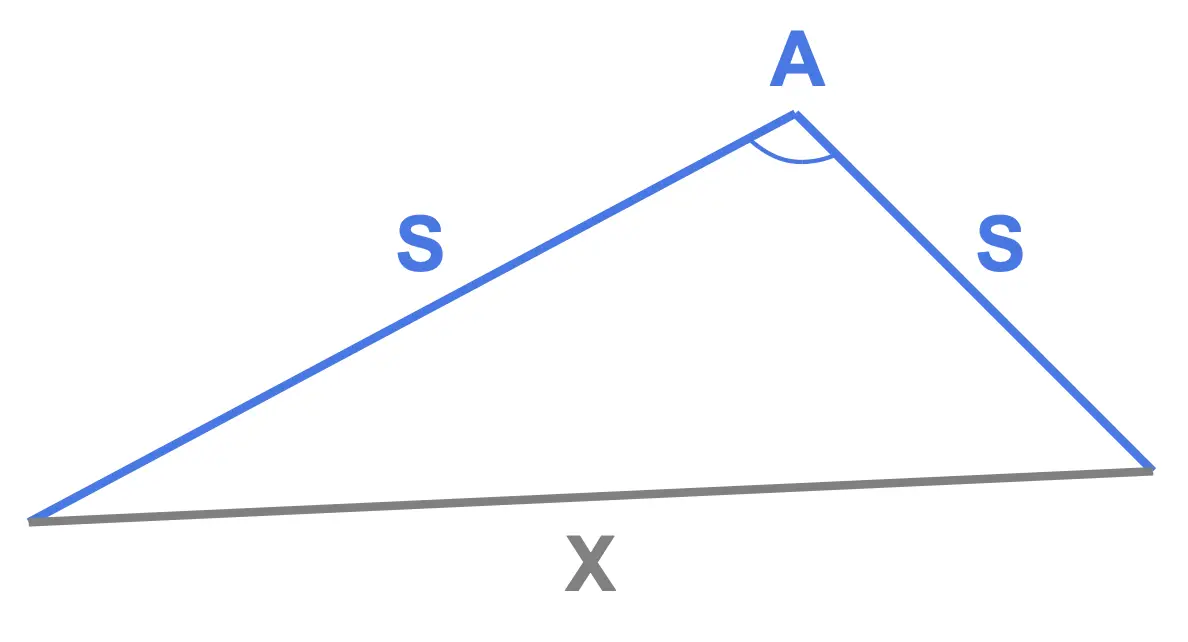
We use the cosine rule to find an unknown side length when we have (or can easily find):
- two side lengths (those are \(a\) and \(b\) in the formula)
- the angle between them (that's \(C\) in the formula)
This is illustrated here where the angles and side labelled in blue correspond to the information we have and the gray X corresponds to the side we'd need to find.
Tutorial: Cosine Rule for Unknown Side
In the following tutorial we learn how to use the Sine Rule to find an unknown side. Watch it to view worked examples.
 Worked Example 1 : Unknown Side
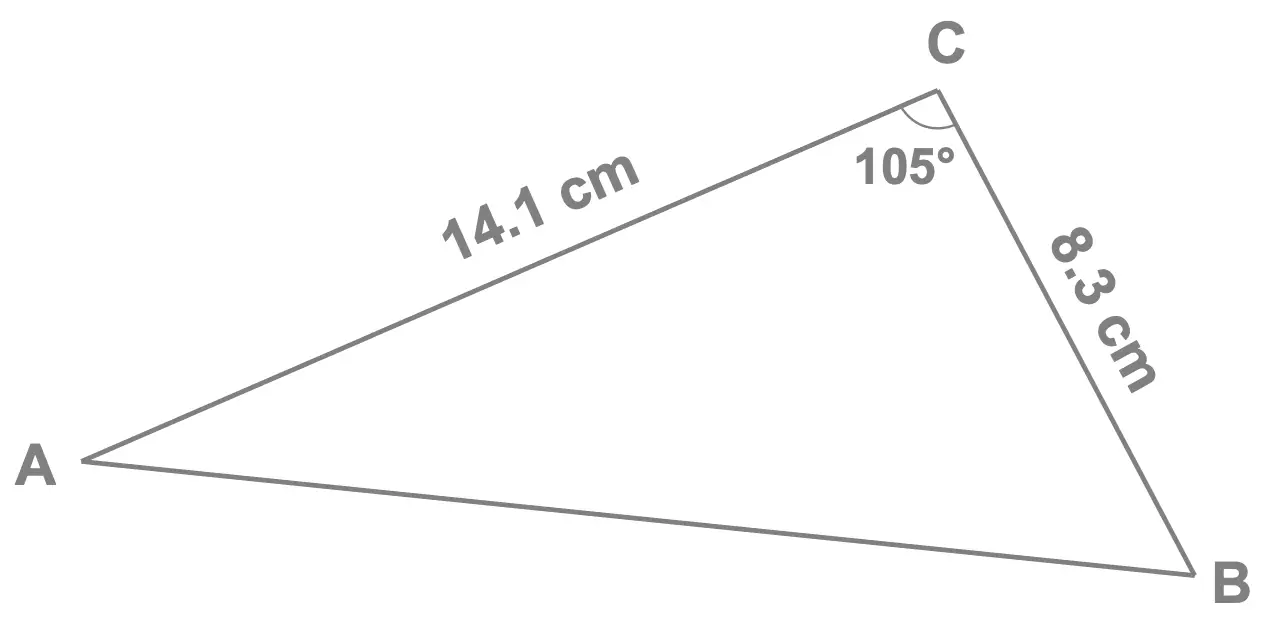
Worked Example 1 : Unknown Side
Consider triangle ABC shown here.
Rounding to 3 significant figures, find the length of \(AB\).
Solution
We start by summarizing the information we have. Here we've colored that information in blue:
- 2 side lengths
- the angle between them
 Applying the cosine rule:
\[AB^2 = AC^2 + BC^2 - 2\times AC \times BC \times cos \begin{pmatrix} 105 \end{pmatrix}\]
Now repalcing \(AC\), \(BC\) and the angle \(C\) by their respective values:
\[\begin{aligned}
AB^2 & = 14.1^2 + 8.3^2 - 2\times 14.1 \times 8.3 \times cos \begin{pmatrix} 105 \end{pmatrix} \\
AB^2 & = 328.27919
\end{aligned}\]
Applying the cosine rule:
\[AB^2 = AC^2 + BC^2 - 2\times AC \times BC \times cos \begin{pmatrix} 105 \end{pmatrix}\]
Now repalcing \(AC\), \(BC\) and the angle \(C\) by their respective values:
\[\begin{aligned}
AB^2 & = 14.1^2 + 8.3^2 - 2\times 14.1 \times 8.3 \times cos \begin{pmatrix} 105 \end{pmatrix} \\
AB^2 & = 328.27919
\end{aligned}\]
 Finally, to find the length \(AB\), we calculate the square root of the answer we just found with our calculator:
\[\begin{aligned}
AB & = \sqrt{328.27919} \\
& = 18.118476 \\
AB & = 18.1 \ \text{cm} \quad \text{(rounded to 3 significant figures)}
\end{aligned}\]
Finally, to find the length \(AB\), we calculate the square root of the answer we just found with our calculator:
\[\begin{aligned}
AB & = \sqrt{328.27919} \\
& = 18.118476 \\
AB & = 18.1 \ \text{cm} \quad \text{(rounded to 3 significant figures)}
\end{aligned}\]
For an Unknown Angle
Given a triangle for which we seel an unknown angle and none of the other angmes are known, we can

Where the side lengths \(a\), \(b\) and \(c\) refer to those on the generic triangle shown here:

When to use the cosine rule
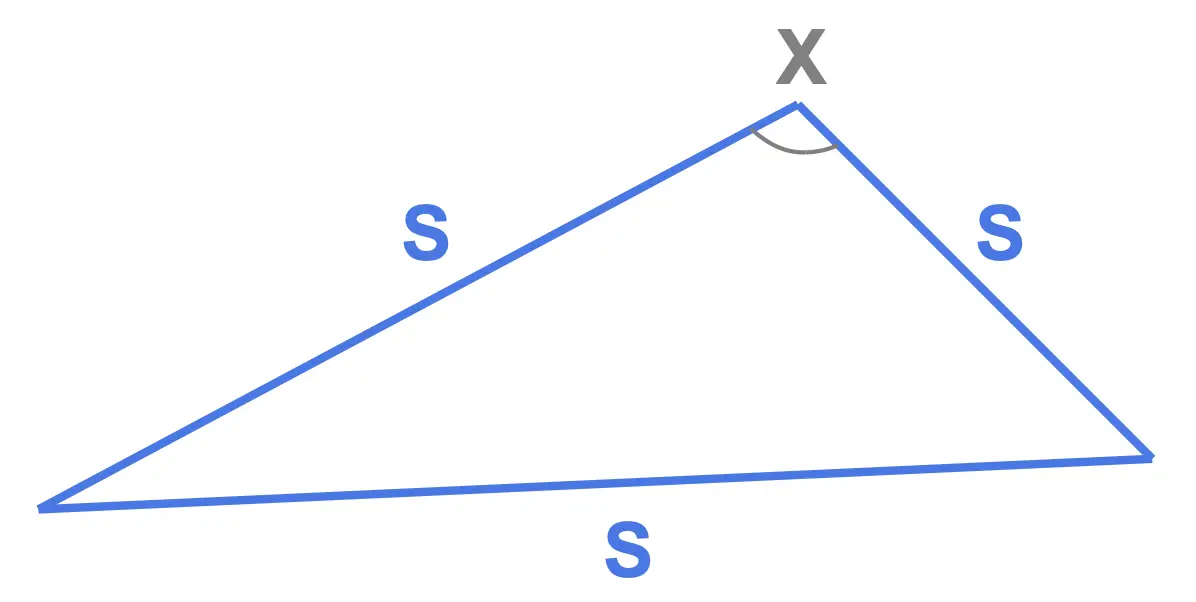
We use the cosine rule to find an unknown angle when we have:
- All 3 side lengths of the triangle
- not a single interior angle
This is illustrated here where the angles and side labelled in blue correspond to the information we have and the gray X corresponds to the angle we may wish to find (although we could have place X opposite either of the 3 sides):
Tutorial: Cosine Rule for Unknown Angle
In the following tutorial we learn how to use the Sine Rule to find an unknown angle. Watch it to view worked examples.
 Worked Example 2 : Unknown Angle
Worked Example 2 : Unknown Angle
Given triangle ABC, shown here, and rounding your answer to 1 decimal place, find the value of the angle marked X.
Solution

- all 3 side lengths
- not a single interior angle
We can therefore use the cosine rule for this unknown angle. Keeping in mind that the side length opposite the angle (that's the 16cm side) is the one that ends-up being subtracting on the expression's numerator, we can write:
\[\begin{aligned}
cosX & = \frac{14^2+18^2-16^2}{2\times 14 \times 18} \\
cosX & = 0.52380952
\end{aligned}\]
Finally using the inverse cosine function, \(cos^{-1}(x)\), on our calculator, we can find the value of angle X:
\[\begin{aligned}
X & = cos^{-1}\begin{pmatrix} 0.52380952 \end{pmatrix} \\
& = 58.411864^{\circ} \\
X & = 58.4^{\circ}
\end{aligned}\]
Scan this QR-Code with your phone/tablet and view this page on your preferred device.
Subscribe Now and view all of our playlists & tutorials.