RadfordMathematics.com

Sine Rule for Unknown Sides & Unknown Angles

The Sine Rule can be used to find unknown sides as well as find unknown angles in triangles that aren't right-angled (it works for right-angled triangles as well).

The sine rule involves side lengths and their opposite angles (we could also say angles and their opposite sides) and to undertstand what the sine rule formula tells us we must be familiar with the generic triangle labelling the formula refer to.

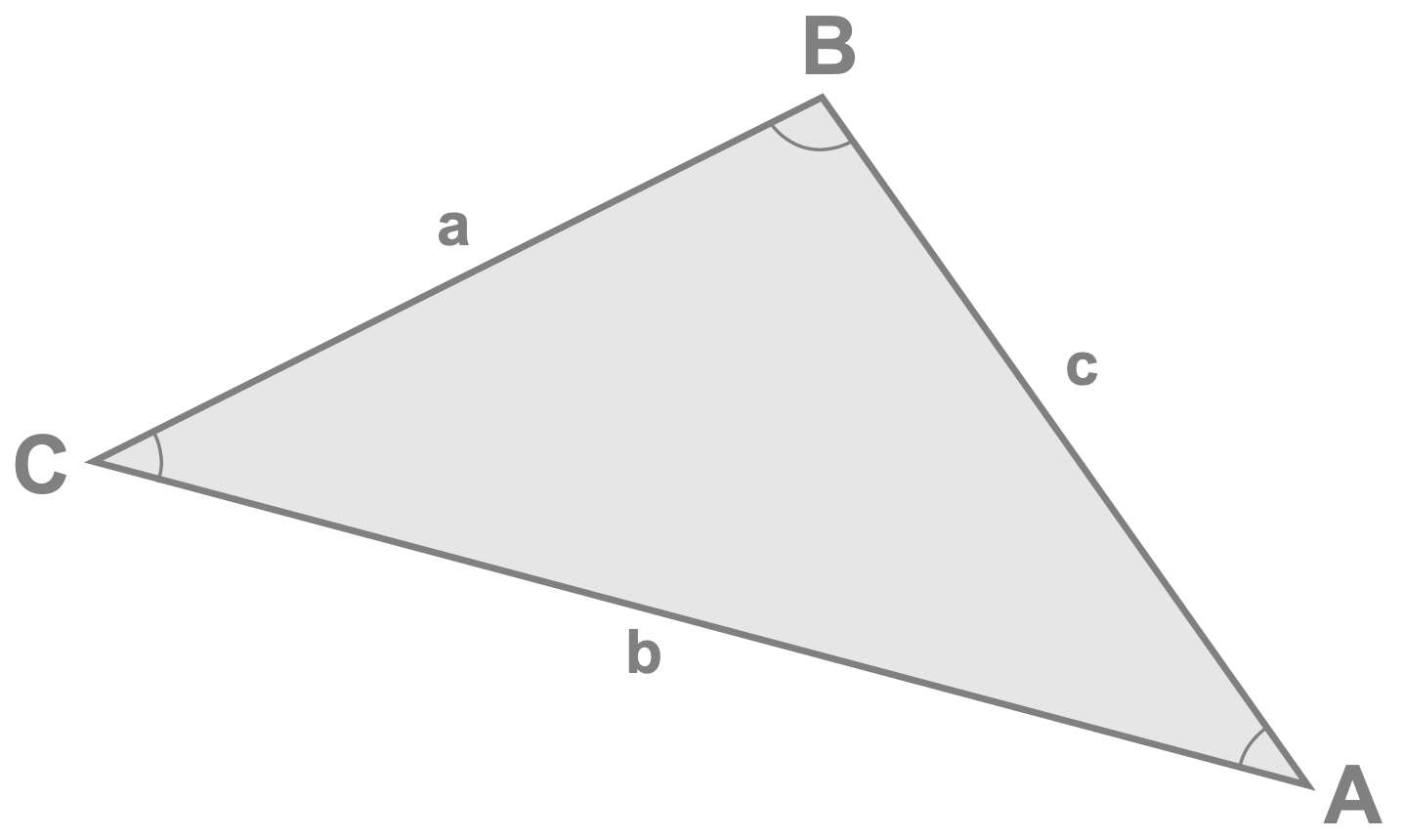
Generic Triangle

  • Side lengths are labelled counter-clockwise, with lower-case letters a, b and c.
  • Angles are labelled as the Upper-Case version of the side length they're opposite to. So angle A refers to the interior angle opposite the side length a, angle B refers to the interior angle opposite the side length b and angle C refers to the interior angle opposite the side length c.

Since the sine rule involves side lengths and their opposite angles, it can be useful to connect each pair as shown here:

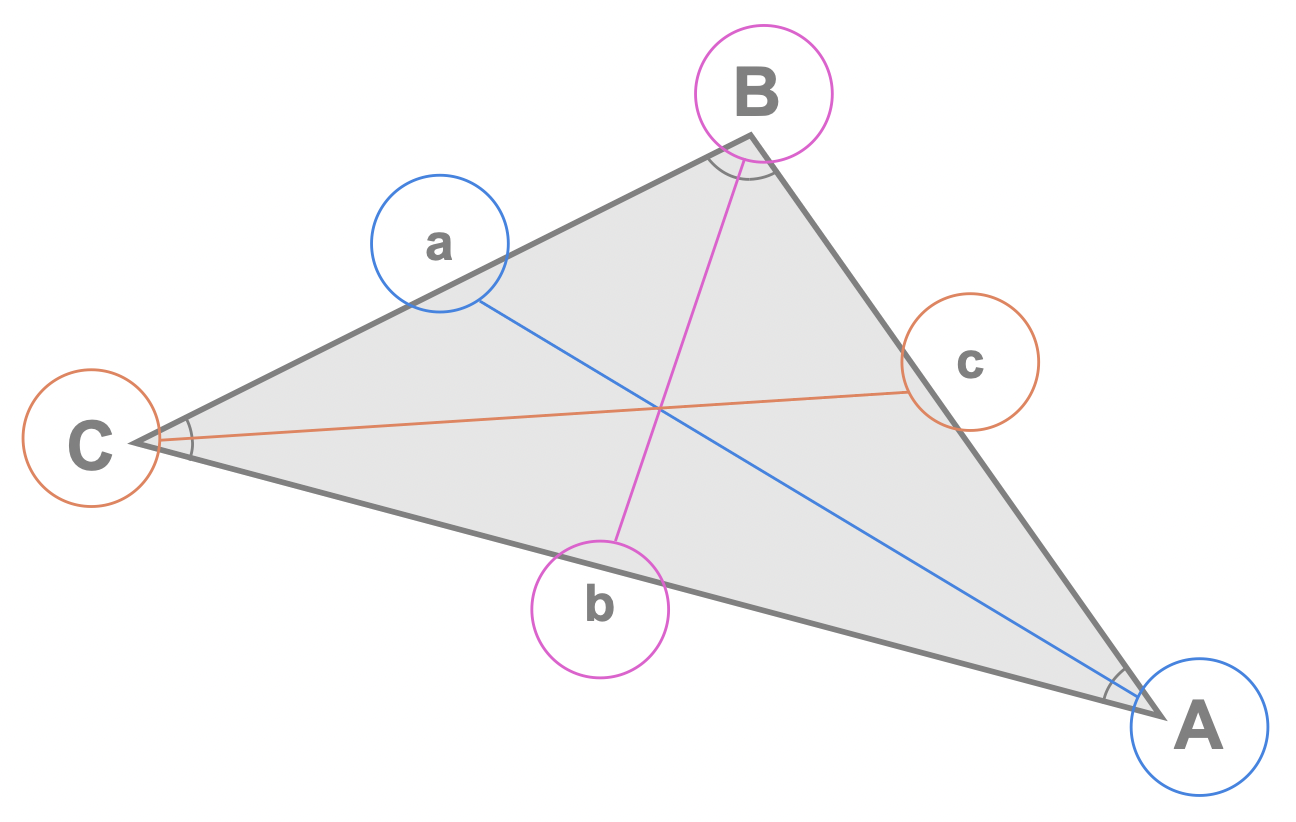
This visual aid can be useful: provided, for 2 pairs of 'side and opposite angle', there is only one unknown : we can use the sine rule; this will become clearer with the worked examples further down.

For an Unknown Side Length

Given a triangle the ratio of each side divided by the sine of its opposite angle is the same throughout the triangle. This fact leads to the sine rule, which (when looking for an unknown side length) can be written:

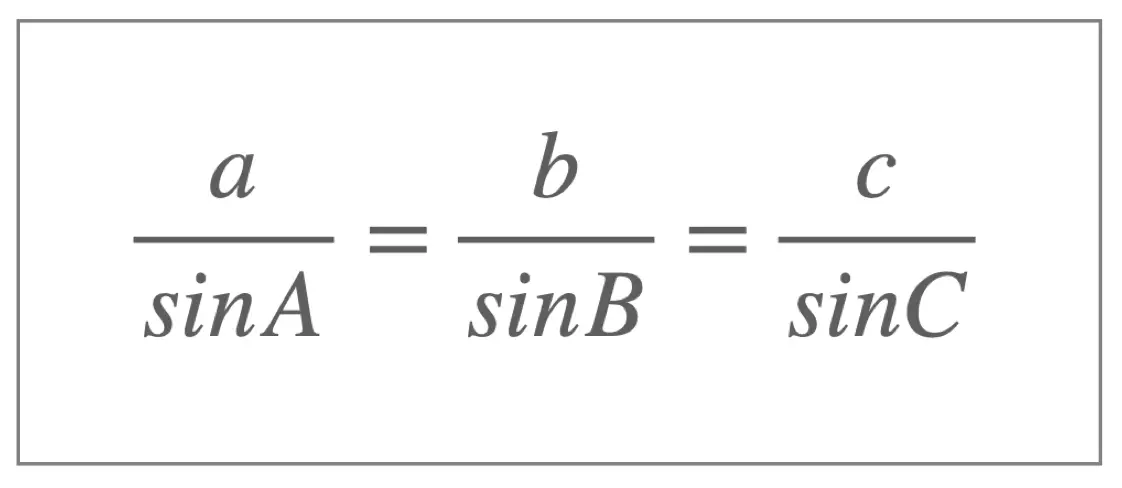
NOTE: another way of saying this is that the ratio 'side length divided by the sine of its opposite angle' is constant throughout a triangle: \[\frac{\text{side length}}{sin\begin{pmatrix} \text{opposite angle}\end{pmatrix}}= \text{constant}\]

When to use the sine rule

We use the sine rule to find an unknown side length when we have (or can easily find):

  • the angle opposite the side we're trying to find
  • any other side length and its opposite angle
This is often refered to as SAA (or AAS) as in Side-Angle-Angle and can also be obtained from ASA as in Angle-Side-Angle (since we'd be able to find the angle opposite the side we have using the fact that all 3 angles must add up to \(180^{\circ}\)).

This is illustrated here where the angles and side labelled in blue correspond to the information we have and the gray X corresponds to the side we'd need to find.

Tutorial: Sine Rule for Unknown Side

In the following tutorial we learn how to use the Sine Rule to find an unknown side. Watch it to view worked examples.

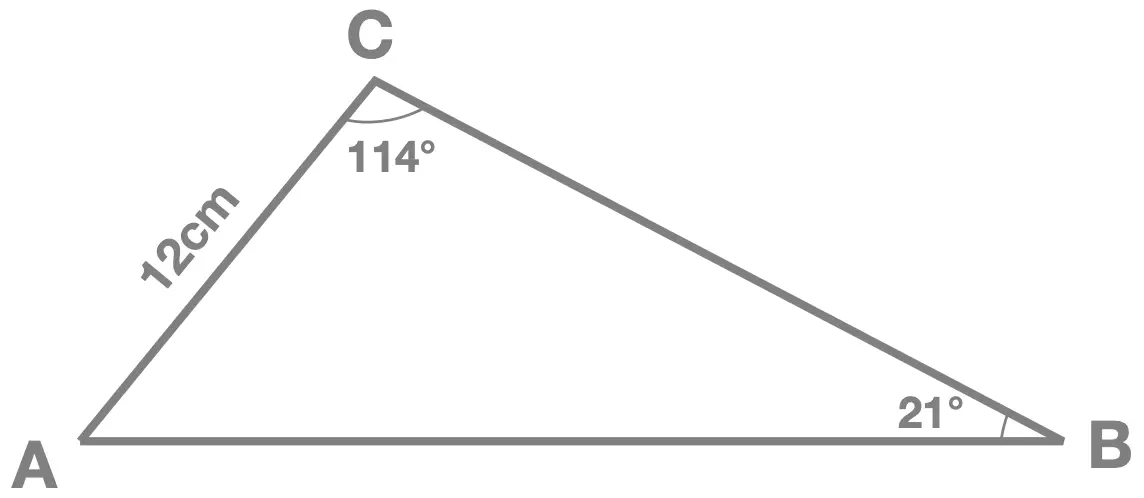Worked Example 1 : Unknown Side

Given triangle ABC, shown here, find the value of the side length AB.

Solution

We start by summarizing the information we have as well as what we're trying to find. We have:

  • a pair : angle and its opposite side length (\(21^{\circ}\) and \(12\)cm)
  • the angle opposite the side we're trying to find (\(114^{\circ}\))

We can therefore use the sine rule to find the side.

Starting from \(\frac{a}{sinA} = \frac{b}{sinB}\) we can write: \[\frac{AB}{sin\begin{pmatrix}114^{\circ} \end{pmatrix}} = \frac{12}{sin\begin{pmatrix}21^{\circ} \end{pmatrix}}\] To find \(AB\) we now multiply both sides by \(sin\begin{pmatrix}114^{\circ} \end{pmatrix} \): \[AB = sin\begin{pmatrix}114^{\circ} \end{pmatrix} \times \frac{12}{sin\begin{pmatrix}21^{\circ} \end{pmatrix}} \]

Finally to find \(AB\) we evaluate this expression with our calculator. We find: \[AB = 30.5902 \ \text{cm}\] Rounding to 3 significant figures: \[AB = 30.6 \ \text{cm}\]

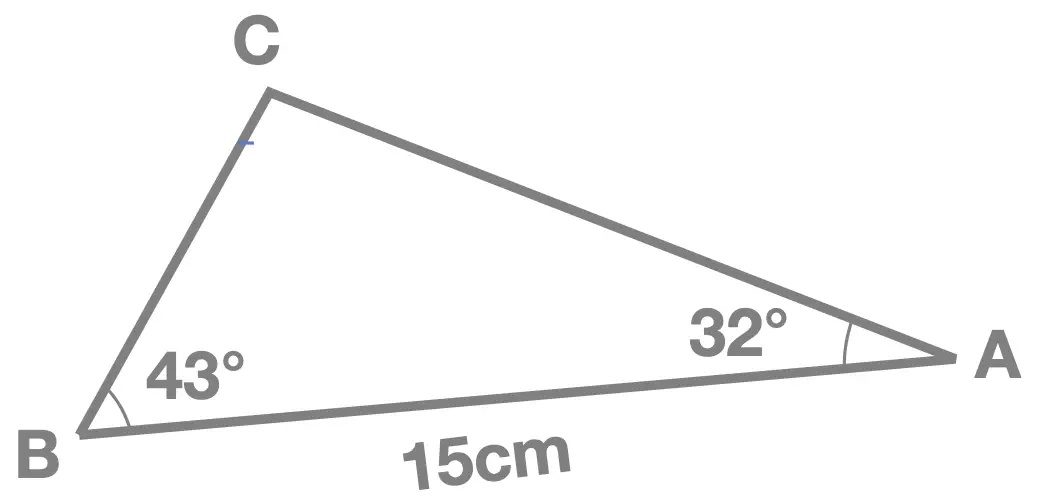Worked Example 2 : Unknown Side

Given triangle ABC, shown here, find the value of the side length AC.

Solution

We start by summarizing the information we have as well as what we're trying to find. We have:

  • two angles, \(43^{\circ}\) and \(32^{\circ}\)
  • the inlcuded side (between the two angles) of \(15cm\)
  • we need to find the side length \(AC\), which is opposite the \(43^{\circ}\) angle.
At first glance, because we don't know the interior angle at \(C\), we may not think we can use the sine rule to find \(AC\). But since interior angles of a triangle add up to \(180^{\circ}\) and since we have the other two interio angles we can quickly find the missing angle: \[\begin{aligned} \text{Interior Angle at C} & = 180^{\circ} - 43^{\circ} - 32^{\circ} \\ & = 137^{\circ} - 32^{\circ} \\ \text{Interior Angle at C} & = 105^{\circ} \end{aligned}\]

We can therefore use the sine rule to find the side.

Starting from \(\frac{a}{sinA} = \frac{b}{sinB}\) we can write: \[\frac{AB}{sin\begin{pmatrix}114^{\circ} \end{pmatrix}} = \frac{12}{sin\begin{pmatrix}21^{\circ} \end{pmatrix}}\] To find \(AB\) we now multiply both sides by \(sin\begin{pmatrix}114^{\circ} \end{pmatrix} \): \[AB = sin\begin{pmatrix}114^{\circ} \end{pmatrix} \times \frac{12}{sin\begin{pmatrix}21^{\circ} \end{pmatrix}} \]

Finally to find \(AB\) we evaluate this expression with our calculator. We find: \[AB = 30.5902 \ \text{cm}\] Rounding to 3 significant figures: \[AB = 30.6 \ \text{cm}\]

For an Unknown Angle

When looking for an unknown angle, the sine rule we saw further-up can be rearranged (flipped over) to write:

When to use the sine rule

We use the sign rule to find an unknown angle when, as we "walk around" the triangle, we have:

  • 2 consecutive side lengths
  • an angle opposite one of those two sides
This is often refered to as SSA (or ASS) as in Side-Side-Angle.

This is illustrated here where the angle and sides labelled in blue correspond to the information we have and the gray X corresponds to the angle we need to find.

Tutorial: Sine Rule for Unknown Angle

In the following tutorial we learn how to use the Sine Rule to find an unknown angle. Watch it to view worked examples.

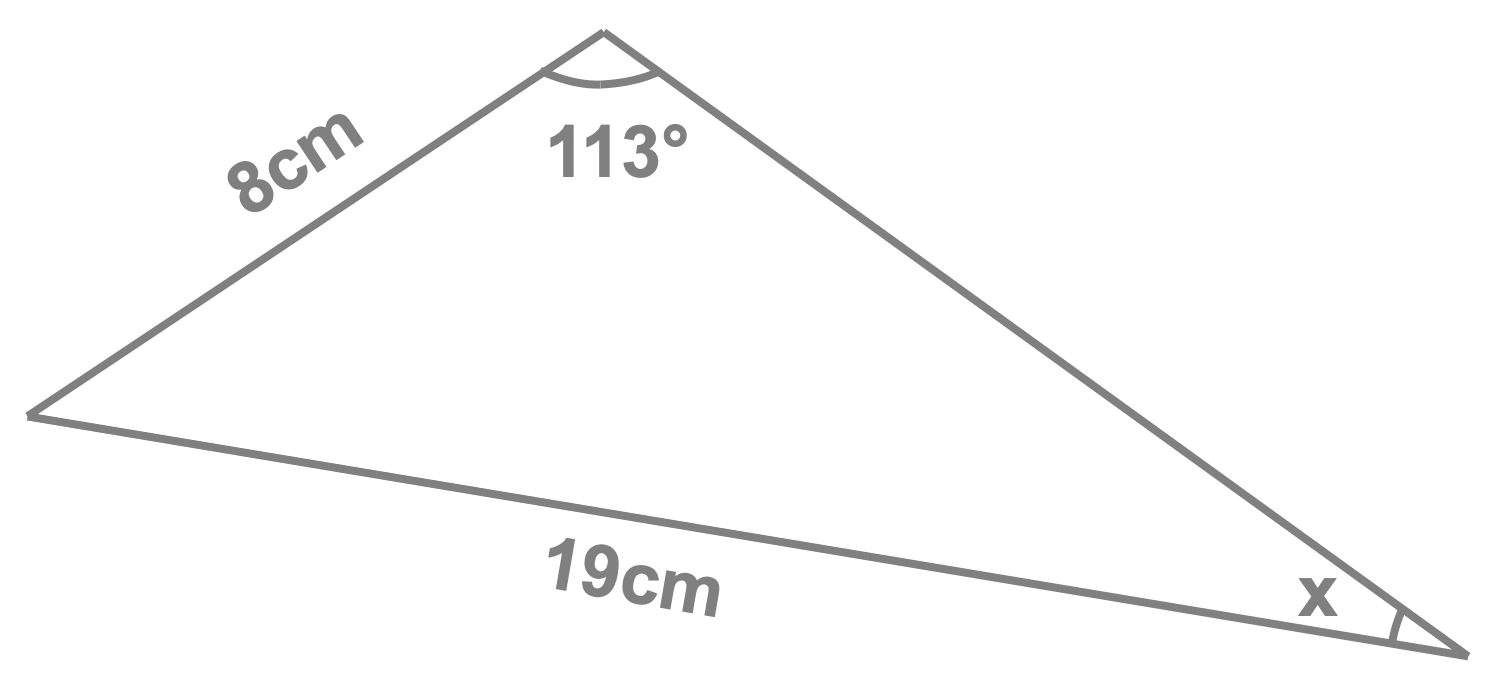Worked Example 3 : Unknown Angle

Given the triangle, shown here, find the value of the angle \(x\).

Solution

We start by summarizing the information we have as well as what we're trying to find. We have:

  • the side length opposite the angle \(x\), which is \(8\)cm long
  • a pair 'side length and its opposite angle', indeed we have a \(19\)cm side length, and its opposite angle \(113^{\circ}\)
    • this is illustrated here, with the pink dashed bubble showing the unknown we're after:
We can therefore use the sine rule and write: \[\frac{sin\begin{pmatrix}x\end{pmatrix}}{8} = \frac{sin\begin{pmatrix}113\end{pmatrix}}{19}\] We now isolate the \(sin\begin{pmatrix}x\end{pmatrix}\) term by multiplying bith sides by \(8\), which leads to: \[sin\begin{pmatrix}x\end{pmatrix} = 8 \times \frac{sin\begin{pmatrix}113\end{pmatrix}}{19}\] Finally, applying the inverse sine function \(sin^{-1}\) to both sides of this equation leads to \(x\): \[x = sin^{-1} \begin{pmatrix}8 \times \frac{sin\begin{pmatrix}113\end{pmatrix}}{19}\end{pmatrix}\]

To evaluate this we use our calculator. In doing so, and rounding to 3 significant figures, we find: \[x = 22.8^{\circ}\]

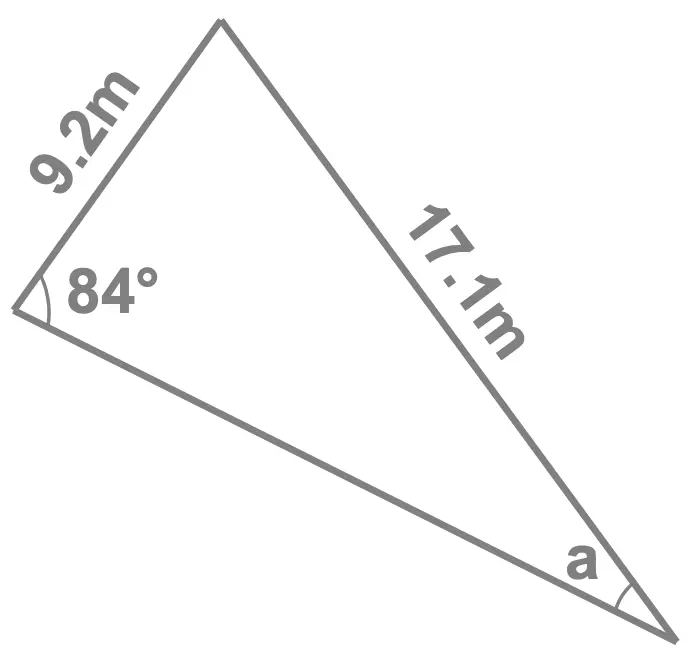Worked Example 4 : Unknown Angle

Given the triangle, shown here, find the value of the angle \(a\).

Solution

We start by summarizing the information we have as well as what we're trying to find. We have:

  • the side length opposite the angle \(x\), which is \(8\)cm long
  • a pair 'side length and its opposite angle', indeed we have a \(19\)cm side length, and its opposite angle \(113^{\circ}\)
    • this is illustrated here, with the pink dashed bubble showing the unknown we're after:
We can therefore use the sine rule and write: \[\frac{sin\begin{pmatrix}x\end{pmatrix}}{8} = \frac{sin\begin{pmatrix}113\end{pmatrix}}{19}\] We now isolate the \(sin\begin{pmatrix}x\end{pmatrix}\) term by multiplying bith sides by \(8\), which leads to: \[sin\begin{pmatrix}x\end{pmatrix} = 8 \times \frac{sin\begin{pmatrix}113\end{pmatrix}}{19}\] Finally, applying the inverse sine function \(sin^{-1}\) to both sides of this equation leads to \(x\): \[x = sin^{-1} \begin{pmatrix}8 \times \frac{sin\begin{pmatrix}113\end{pmatrix}}{19}\end{pmatrix}\]

To evaluate this we use our calculator. In doing so, and rounding to 3 significant figures, we find: \[x = 22.8^{\circ}\]


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.