RadfordMathematics.com

LABELLING SIDE LENGTHS in RIGHT ANGLE TRIANGLES

In this section we learn how to label side lengths in a right angle triangle.

Given a right angle triangle, like the one shown here, its sides are named either:

  • Hypotenuse,
  • Adjacent, or
  • Opposite

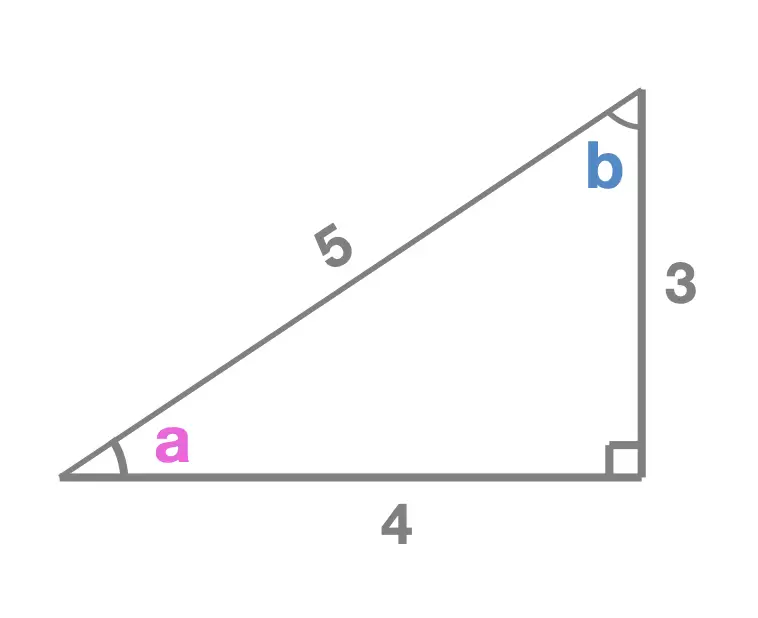
Like every right angle triangle, it has two acute interior angles, labelled \(a\) and \(b\).

Looking at the triangle we see here, we have no trouble in seeing that the hypotenuse is the side of length \(5\), the side length opposite the right angle.

On the other hand, the side we call adjacent and the side we call opposite depends entirely on whether we're focusing on angle \(a\) or \(b\).

Tutorial: Labelling Sides in Right Angle Triangles

In the following tutorial we learn how to label the sides in a right angle triangle.

HOW TO LABEL SIDE LENGTHS

  • HYPOTENUSE

    By definition the hypotenuse is the side opposite the right angle. Since there is only one right angle in a right angle triangle, the hypotenuse "never changes", regardless of whether we are focusing on interior angle \(a\) or \(b\) it will always be the side length opposite the right angle and is the longest side of the right angle triangle.

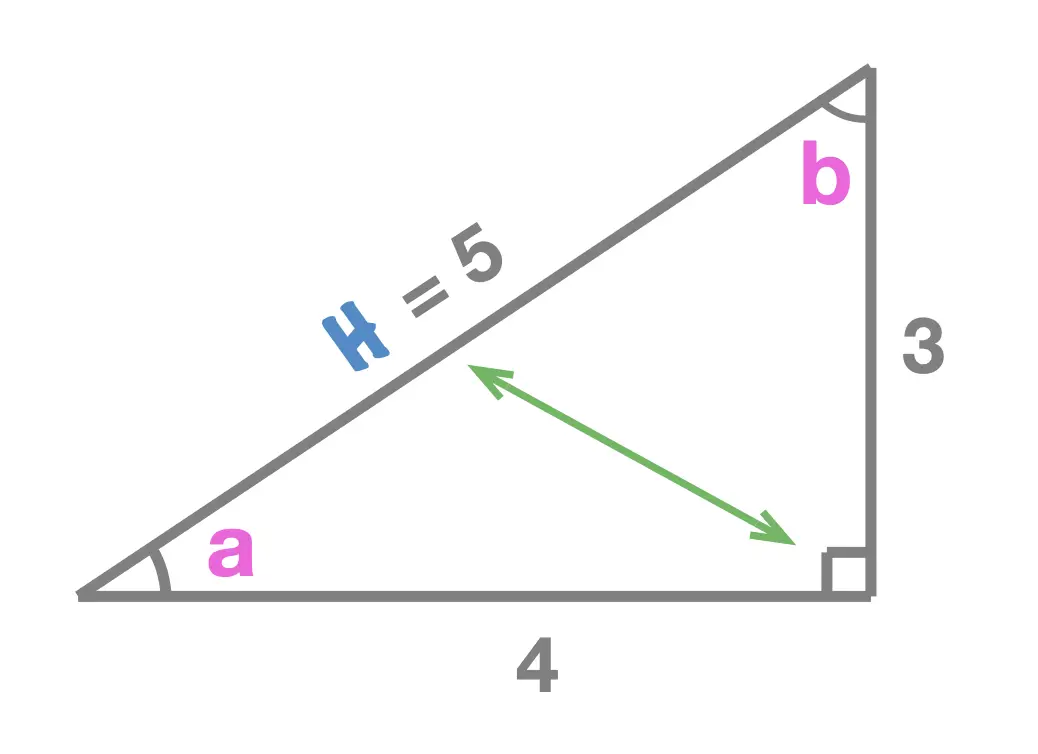
  • ADJACENT & OPPOSITE

    Unlike the hypotenuse, the adjacent and opposite side lengths depend on the interior angle we're focusing on. This is illustrated in the diagrams we see here:

    • relative to angle \(a\)

      We can see that the:
      • adjacent side is of length \(4\), \(A = 4\)
      • opposite side is of length \(3\), \(O = 3\)

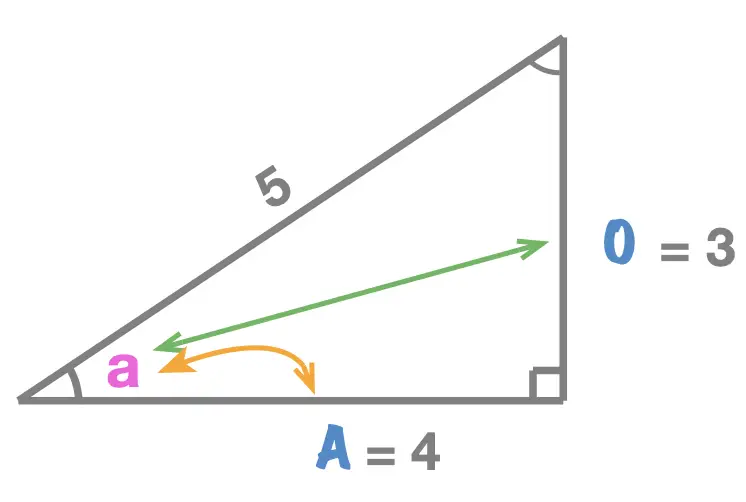
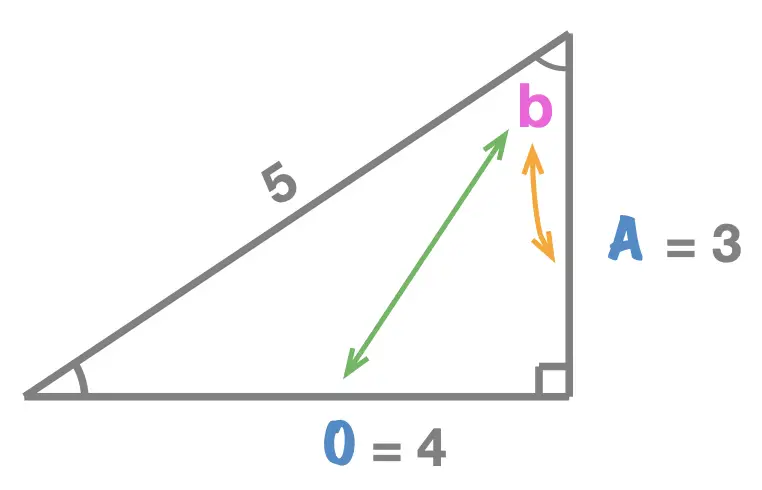
    • relative to angle \(b\)

      We can see that the:
      • adjacent side is of length \(3\), \(A = 3\)
      • opposite side is of length \(4\), \(O = 4\)

Exercise 1

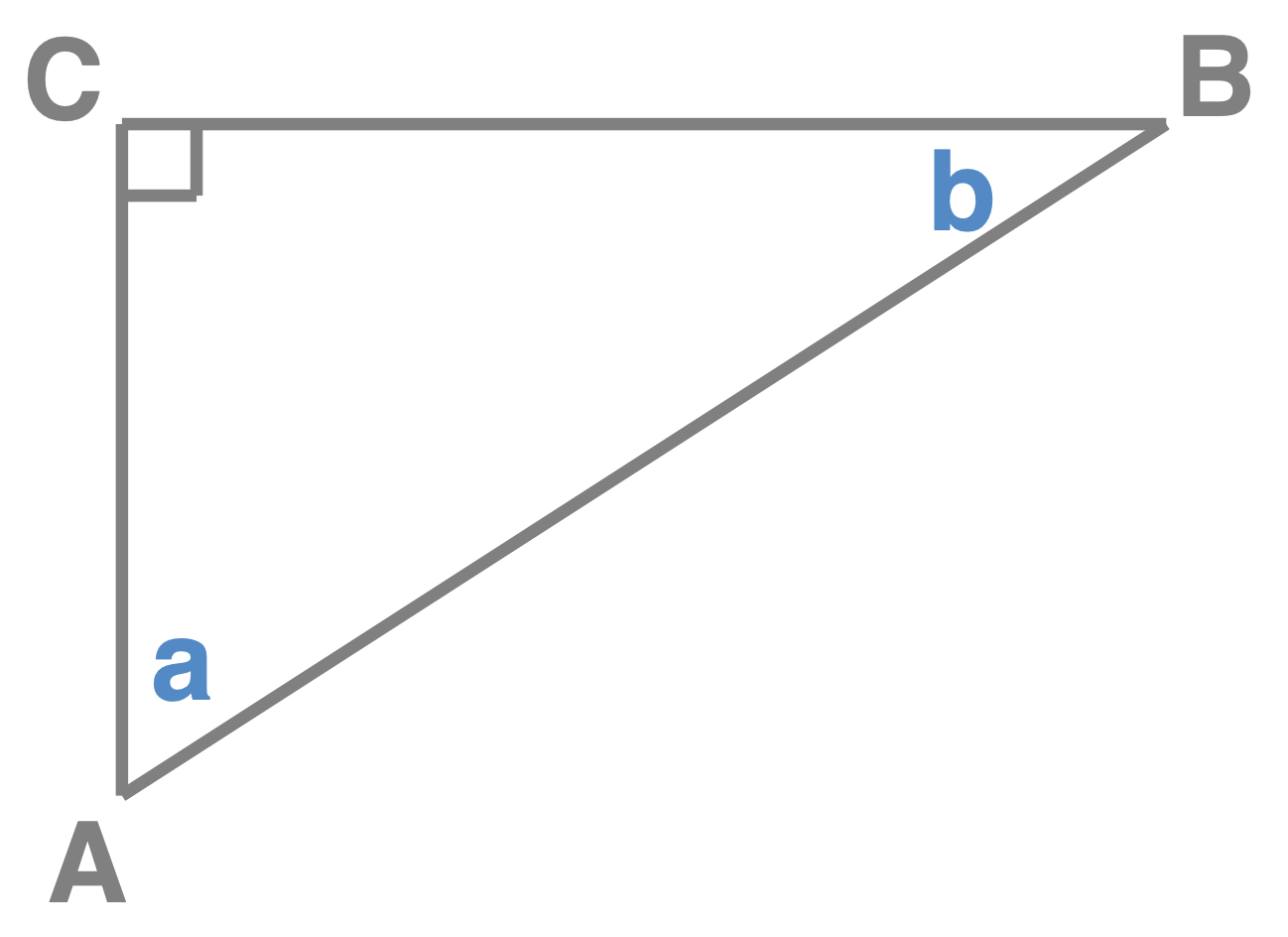
Given the right angle triangle \(ABC\) shown here, name the:

  1. Hypotenuse
  2. Adjacent side to \(b\)
  3. Opposite side to \(a\)
  4. Opposite side to \(b\)
  5. Adjacent side to \(a\)

Note: this exercise, as well as exercise 2, can be downloaded as a worksheet to practice with: Worksheet 1

Solution Without Working

  1. Hypotenuse is \(AB\).
  2. Adjacent side to \(b\) is \(BC\).
  3. Opposite side to \(a\) is \(BC\).
  4. Opposite side to \(b\) is \(AC\).
  5. Adjacent side to \(a\) is \(AC\)

Exercise 2

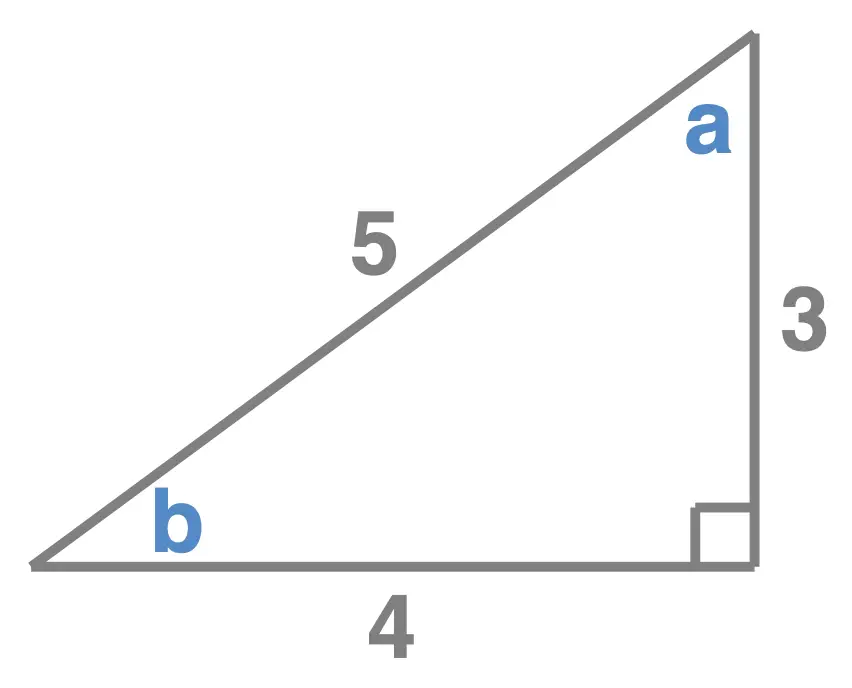
Given the right angle triangle shown here, state the length of:

  1. the side opposite angle \(a\)
  2. the side opposite angle \(b\)
  3. the hypotenuse
  4. the side adjacent to angle \(b\)
  5. the side adjacent to angle \(a\)

Note: this exercise, as well as exercise 1 can be downloaded as a worksheet to practice with: Worksheet 1

Solution Without Working

  1. the length of the opposite to \(a\) is \(4\)
  2. the length of the opposite to \(b\) is \(3\)
  3. the length of the hypotenuse \(5\)
  4. the length of the adjacent to \(b\) is \(4\)
  5. the length of the adjacent to \(a\) is \(3\)


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.