Unknown Side Lengths in Right Angle Triangles - SOH CAH TOA
(Trigonometric Ratios)
In this section we learn how to use SOH CAH TOA to find unknown side lengths in right angle triangles.
What You'll find here:
- We start this section by reminding ourselves of the meaning of SOH CAH TOA
- We write a three step method for finding the unknown side lengths, that will always work (do make a note of it).
- We learn how to use the three step method, notes and tutorials, for the two scenarios we can encounter when trying to find an unknown side length.
- Practice exercises, that can be downloaded as a .pdf worksheet.
Method
Given a right angle triangle, the method for finding an unknown side length, can be summarized in three steps:
- Step 1: Label the side lengths, relative to the given interior (acute) angle, using "A", "O" and "H" (label both the given side length as well as the one you're trying to find).
- Step 2: Using the labels, made in step 1, look for the only one of the words "SOH", "CAH", or "TOA" that contains both of the letters "O" and "H", or "A" and "H", or "O" and "A". Write the corresponding trigonometric ratio for the unknown angle; \(sin(a) = \frac{O}{H}\), \(cos(a) = \frac{A}{H}\), or \(tan(a) = \frac{O}{A}\).
- Step 3: replace the letters, "O" and "H", or "A" and "H", or "O" and "A", by their actual values and solve for \(x\).
Scenario 1: unknown side, \(x\), on the numerator
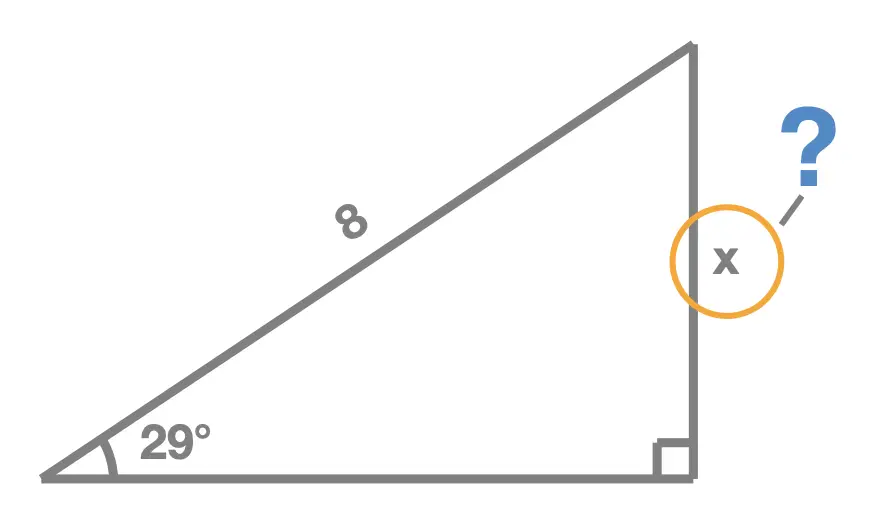
The first scenario we learn about is the one illsutrated here.
- Step 1: label the side lengths relative to the given interior (acute) angle. We can see that relative to the \(29^{\circ}\) the side lengths, \(x\) and \(8\), are the Opposite and the Hypotenuse. So we label them "O" and "H".
- Step 2: using the labels "O" and "H", that we found in step 1, we choose the only one of the three words, SOH CAH TOA, that contains both of those letters. We quickly see that corresponds to SOH, which tells us that: \[sin(29) = \frac{O}{H}\]
(\(x\) is on the numerator)
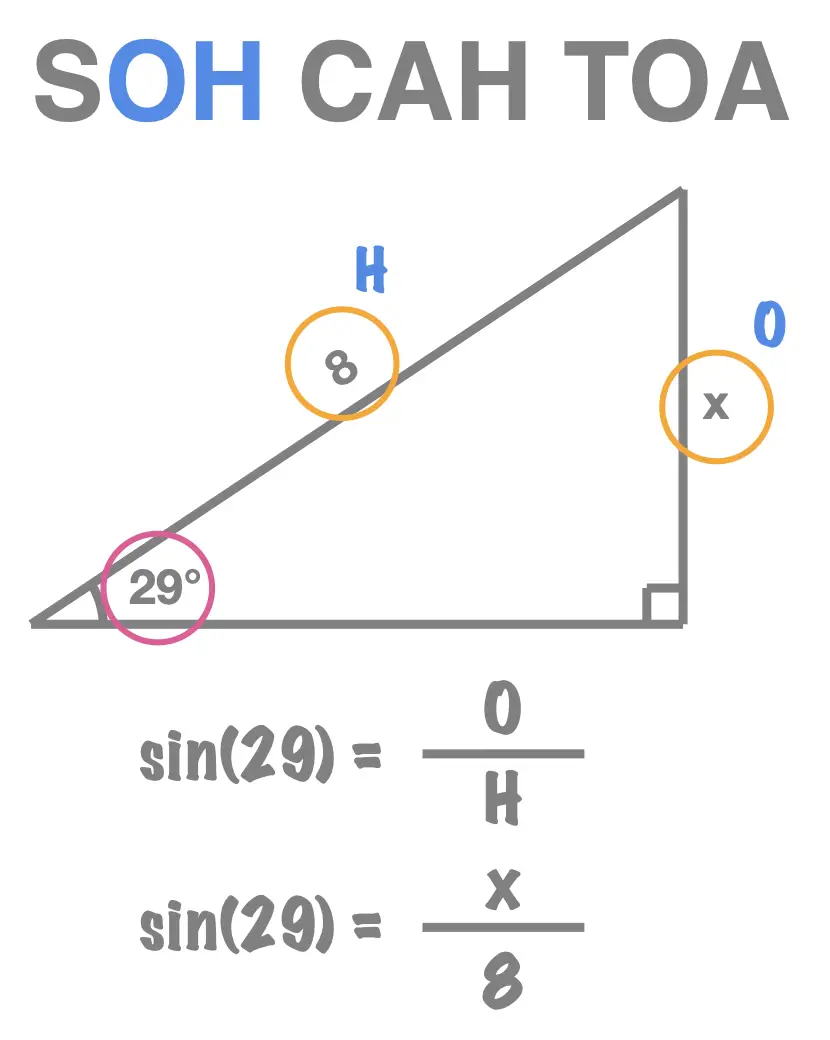
- Step 3: replace O and H by their respective values, \(x\) and \(8\), and solve for \(x\). We have \(sin(29) = \frac{O}{H}\), which becomes: \[sin(29) = \frac{x}{8}\] Multiplying both sides of this equation by \(8\) leads to: \[8\times sin(29) = x\] which can be read, and re-written, from right to left to write: \[x = 8\times sin(29)\] Finally, using a calculator to evaluate \(8\times sin(29)\), rounded to 2 decimal places, we find: \[x = 3.89\]
Tutorial 1:
In the following tutorial we learn how to deal with the simpler scenario in which the unknown side length ends-up on the trigonometric ratio's numerator.
This makes the required algebra, for finding \(x\), relatively simple (all we had to do was multiply by \(8\) to find an expression for \(x\)).
We'll be seeing, in scenario 2, that this won't always be the case. Indeed, in the more complicated cases: \(x\) will be on the denominator and it will require a little more algebra to find an expression for \(x\).
Scenario 2: unknown side, \(x\), on the denominator
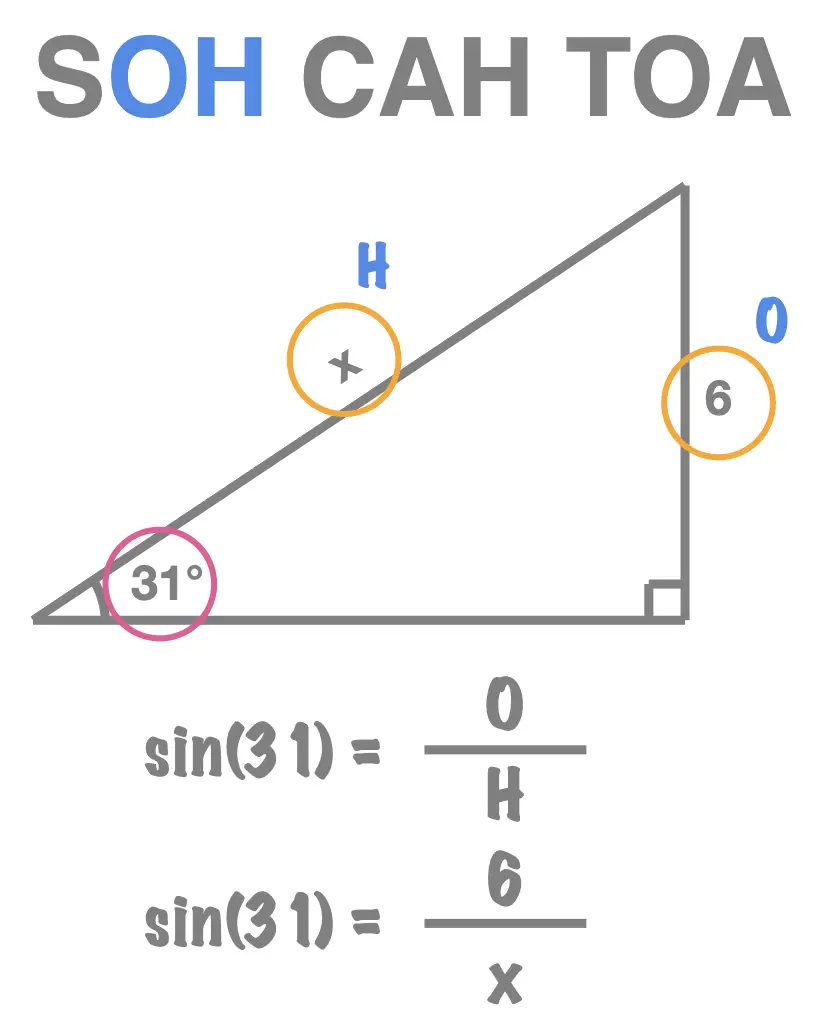
The second scenario we learn about is the one illsutrated here.
- Step 1: label the side lengths relative to the given interior (acute) angle. We can see that relative to the \(31^{\circ}\) the side lengths, \(6\) and \(x\), are the Opposite and the Hypotenuse. So we label them "O" and "H".
- Step 2: using the labels "O" and "H", that we found in step 1, we choose the only one of the three words, SOH CAH TOA, that contains both of those letters. We quickly see that corresponds to SOH, which tells us that: \[sin(31) = \frac{O}{H}\]
- Step 3: replace O and H by their respective values, \(x\) and \(8\), and solve for \(x\). We have \(sin(31) = \frac{O}{H}\), which becomes: \[sin(31) = \frac{6}{x}\] Multiplying both sides of this equation by \(x\) leads to: \[x.sin(31) = 6\] Now, dividing both sides of this equation by \(sin(31)\) leads to: \[x = \frac{6}{sin(31)}\] Finally, using a calculator to evaluate \(\frac{6}{sin(31)}\), rounded to 2 decimal places, we find: \[x = 11.65\]
This makes the required algebra, for finding \(x\), relatively simple (all we had to do was multiply by \(8\) to find an expression for \(x\)).
We'll be seeing, in scenario 2, that this won't always be the case. Indeed, in the more complicated cases: \(x\) will be on the denominator and it will require a little more algebra to find an expression for \(x\).
\(x\) is on the denominator
Tutorial 2:
In the following tutorial we learn how to deal with the simpler scenario in which the unknown side length ends-up on the trigonometric ratio's numerator.
If you feel confident to start working on exercises now, scroll down to work through the exercise further down.
Otherwise make sure to watch this "summary" tutorial, in which we review the two methods for finding uknown side lengths in right angle triangles.
Tutorial 3: Summary - Finding Unknown Side Lengths using SOH CAH TOA
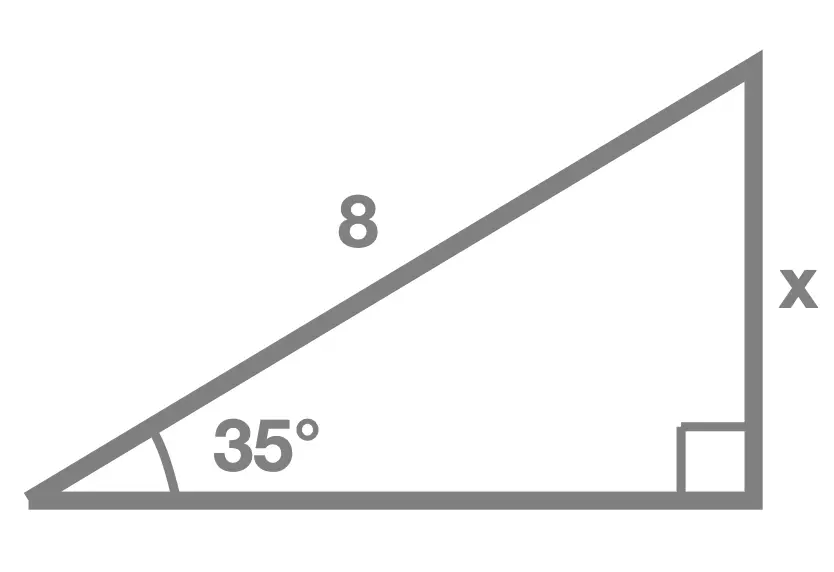
Exercise 1
In each of the following right angle triangles, find the unknown side length marked x:
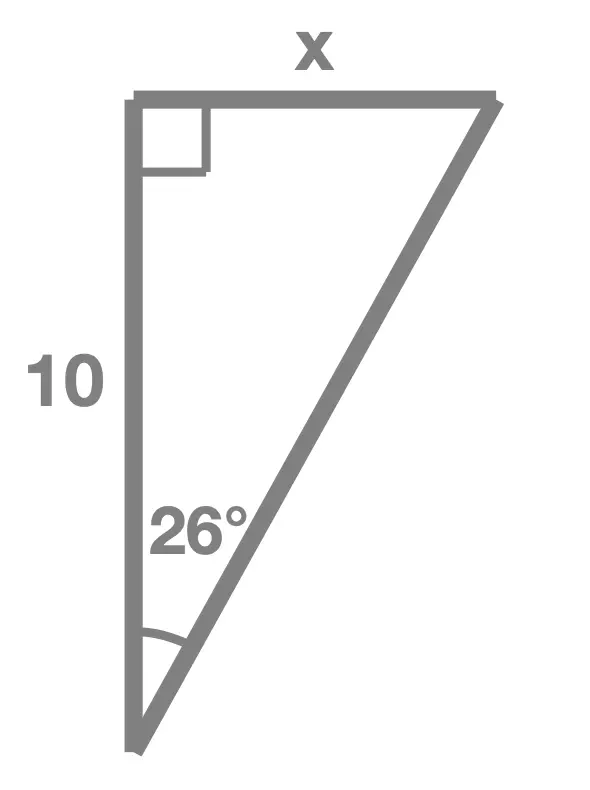
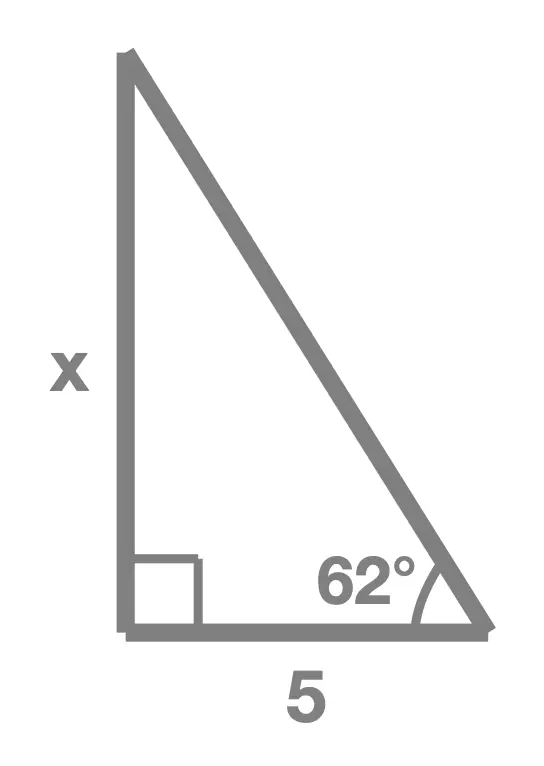
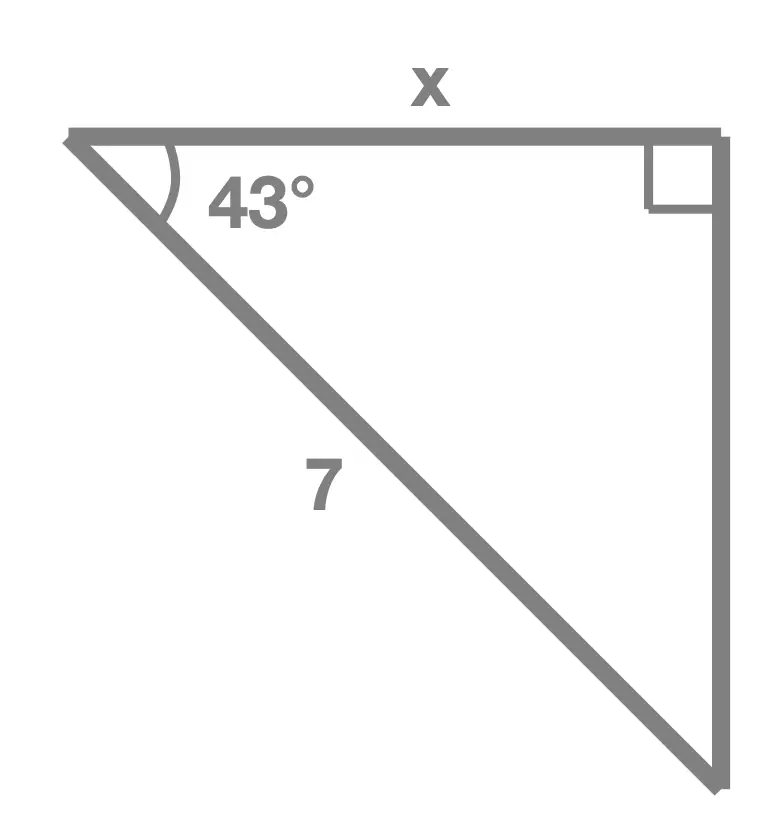
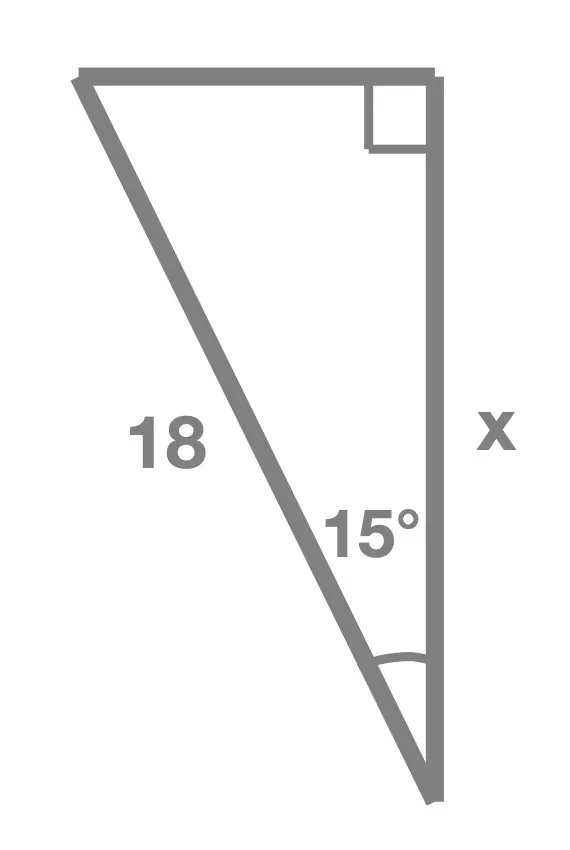
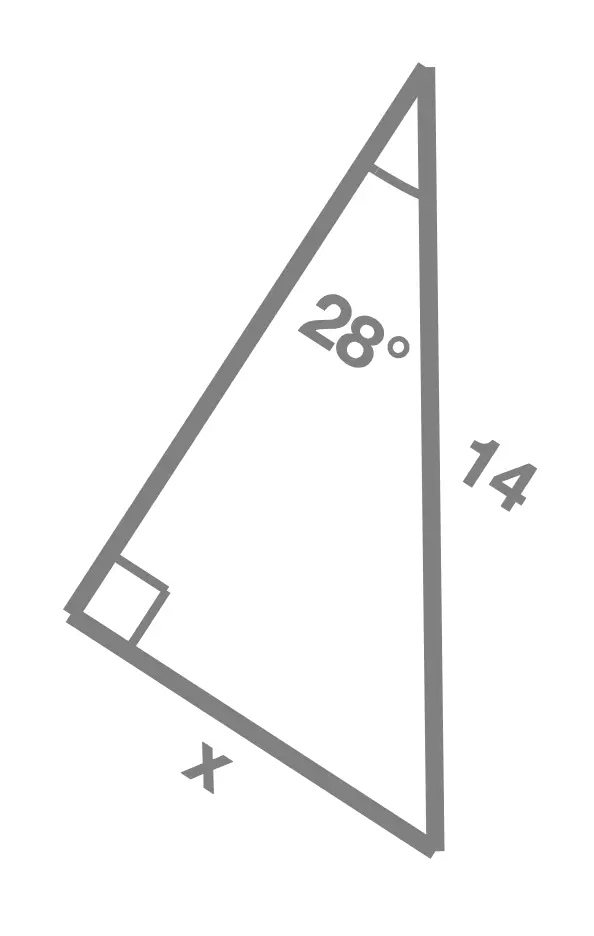
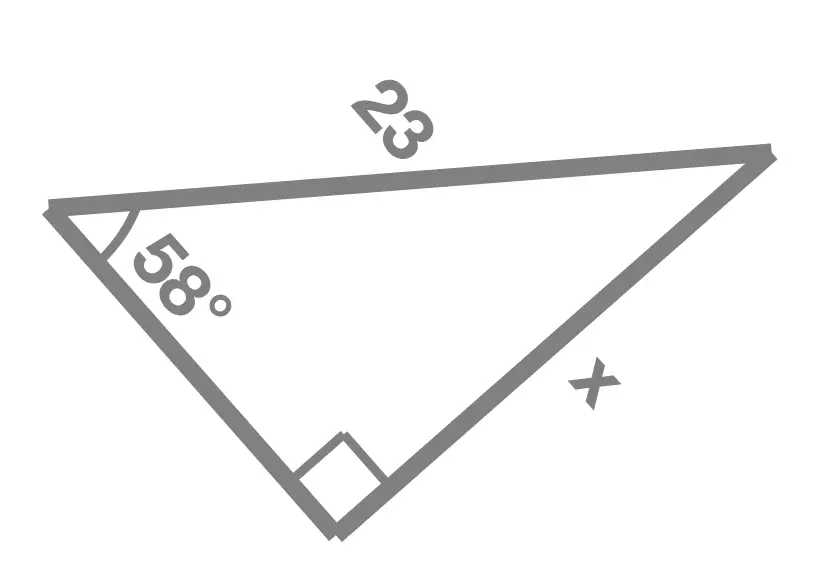
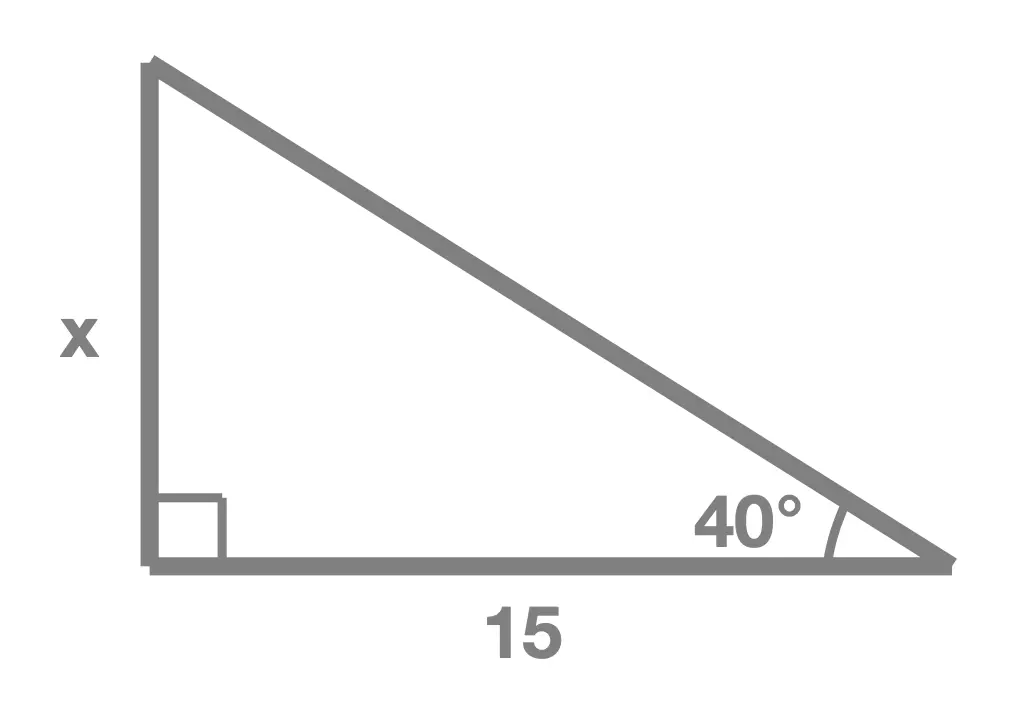
Solution Without Working
- \(x = 4.59\)
- \(x = 4.88\)
- \(x = 9.40\)
- \(x = 5.12\)
- \(x = 17.39\)
- \(x = 6.57\)
- \(x = 19.51\)
- \(x = 12.59\)
Tutorial 2: the "trickier scenario"
In the following tutorial we learn how to deal with the scenario in which the unknown side length ends-up on the trigonometric ratio's denominator.
Exercise 2
In each of the following right angle triangles, find the unknown side length marked x:
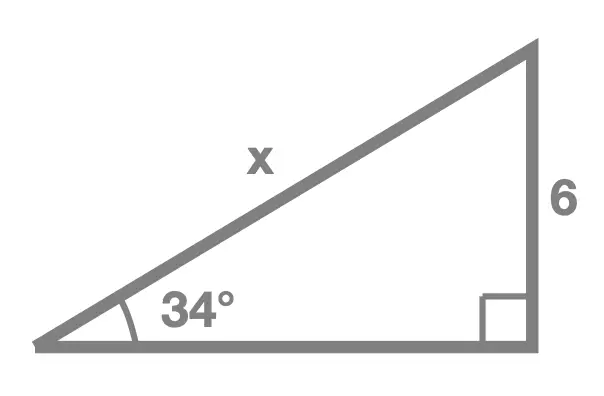
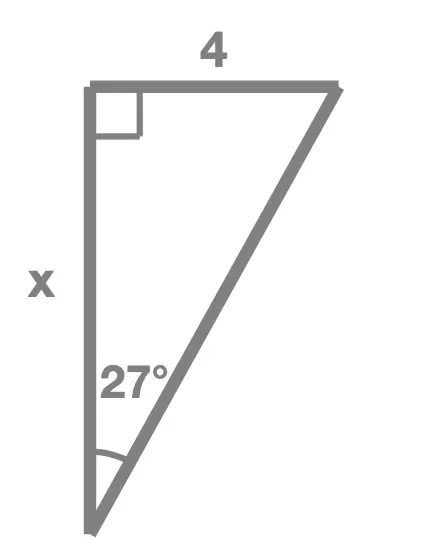
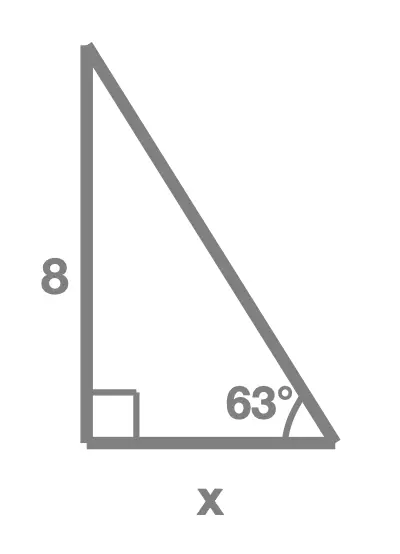
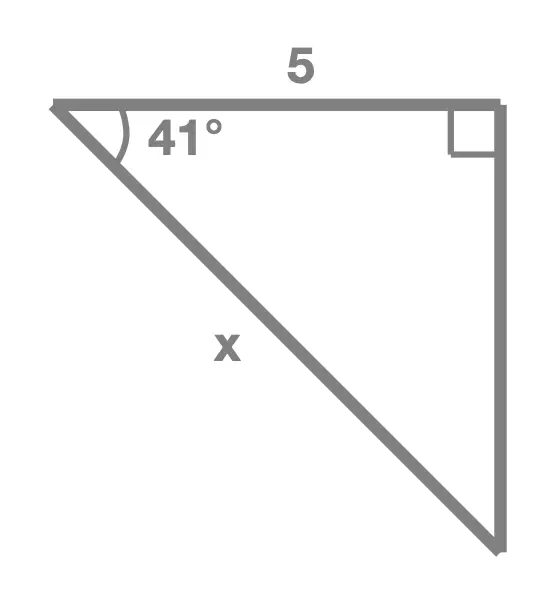
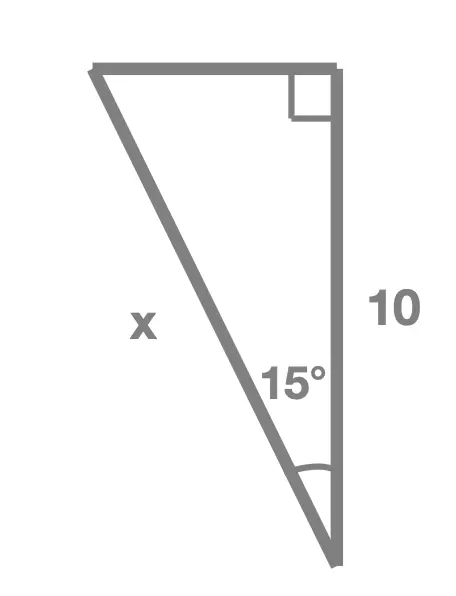
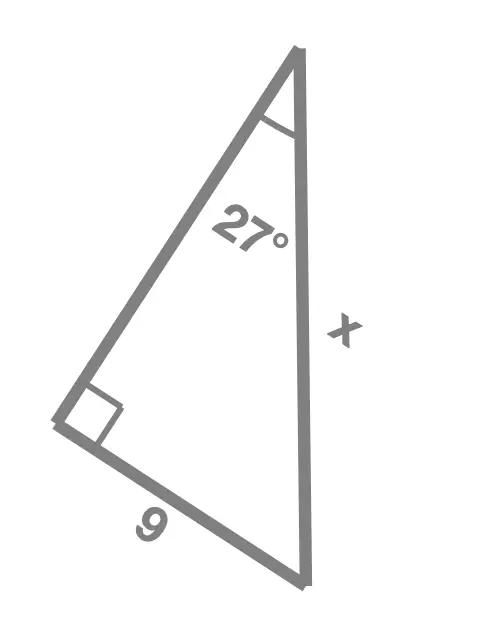
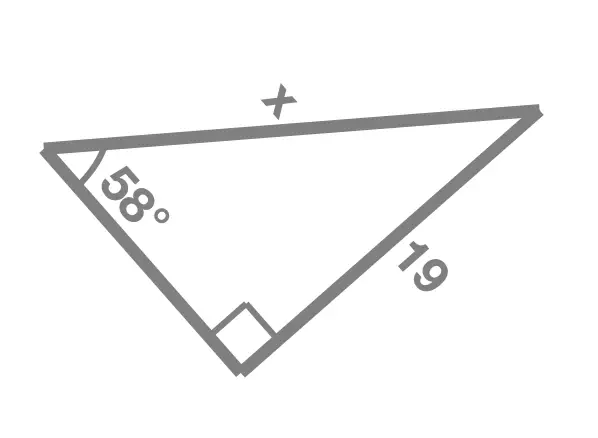
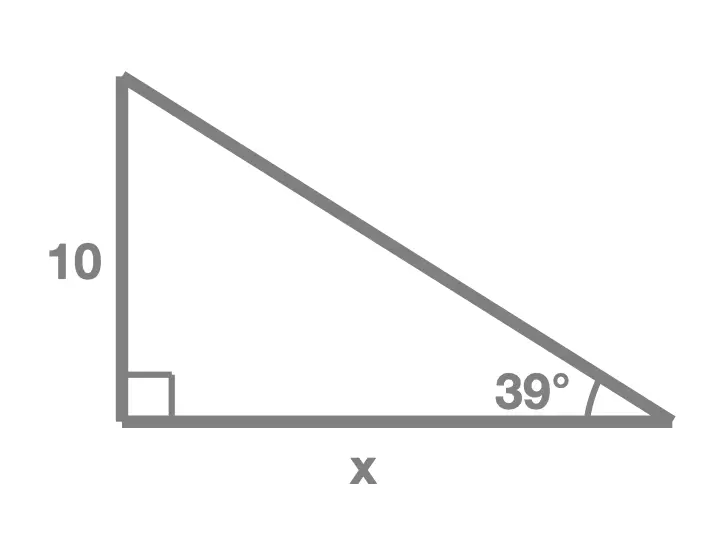
Solution Without Working
- \(x = 10.73\)
- \(x = 7.85\)
- \(x = 4.08\)
- \(x = 6.625\)
- \(x = 10.35\)
- \(x = 19.82\)
- \(x = 22.40\)
- \(x = 12.35\)
Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.