TRIGONOMETRIC RATIOS & SOH CAH TOA
In this section we learn about the trigonometric ratios as well as SOH CAH TOA, which is an acronym for memorizing the ratios.
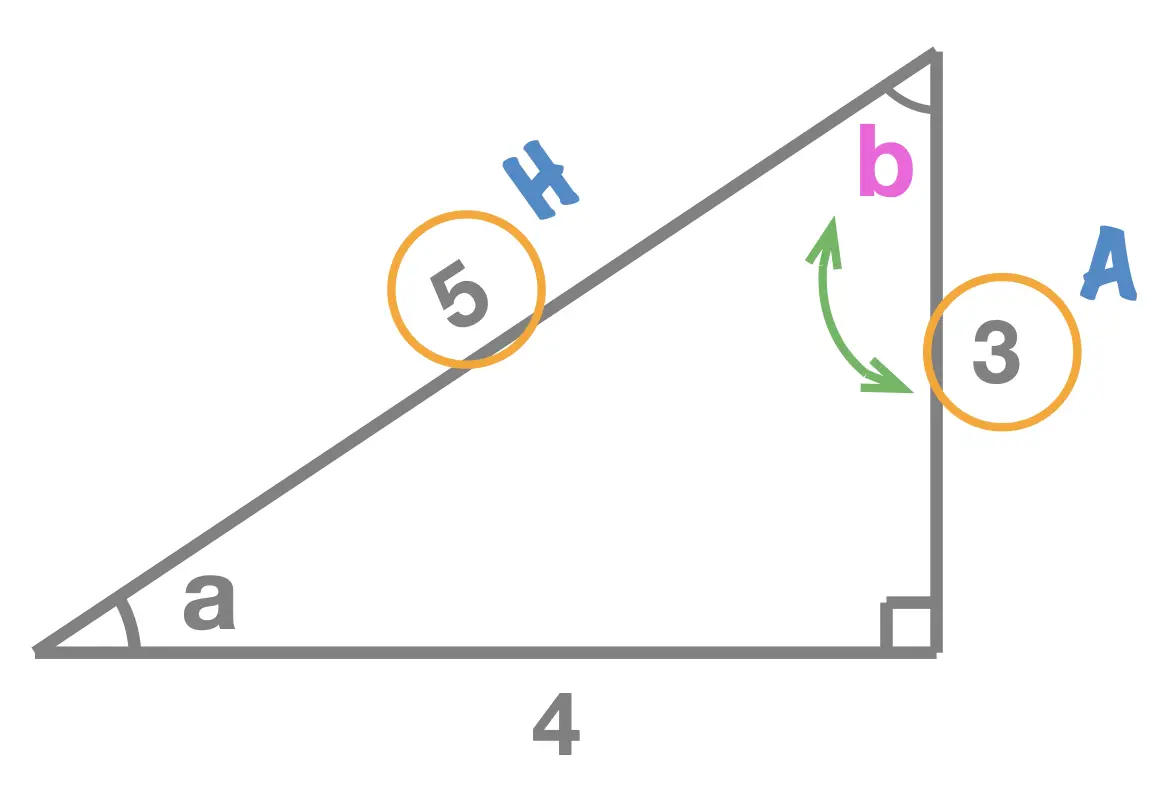
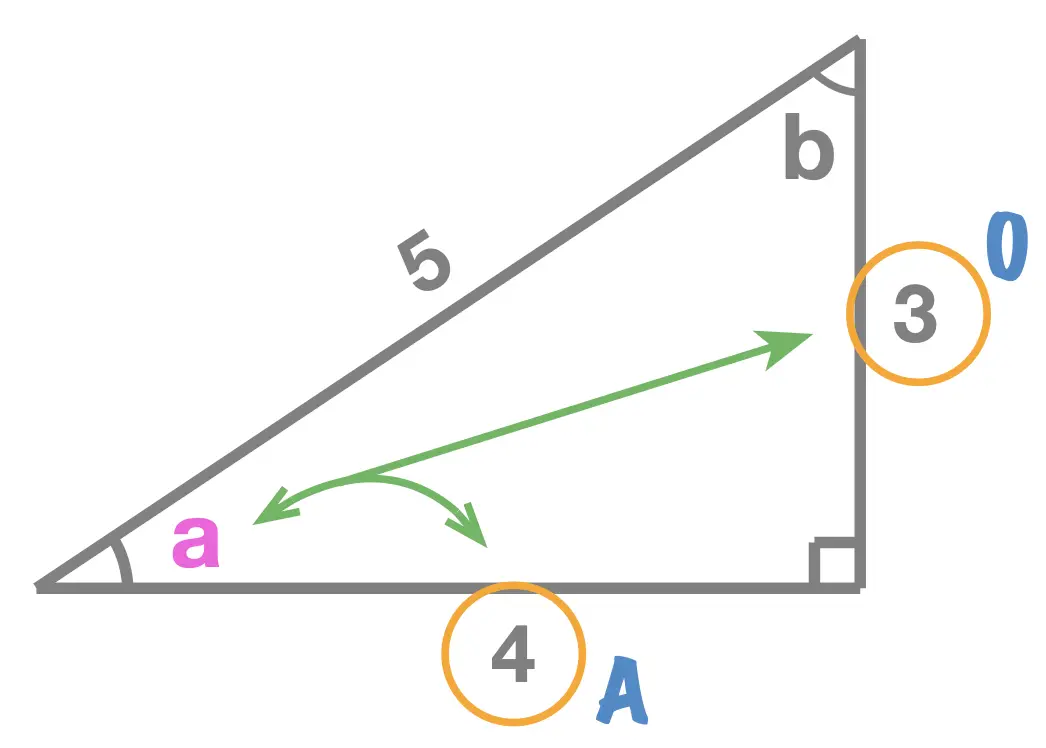
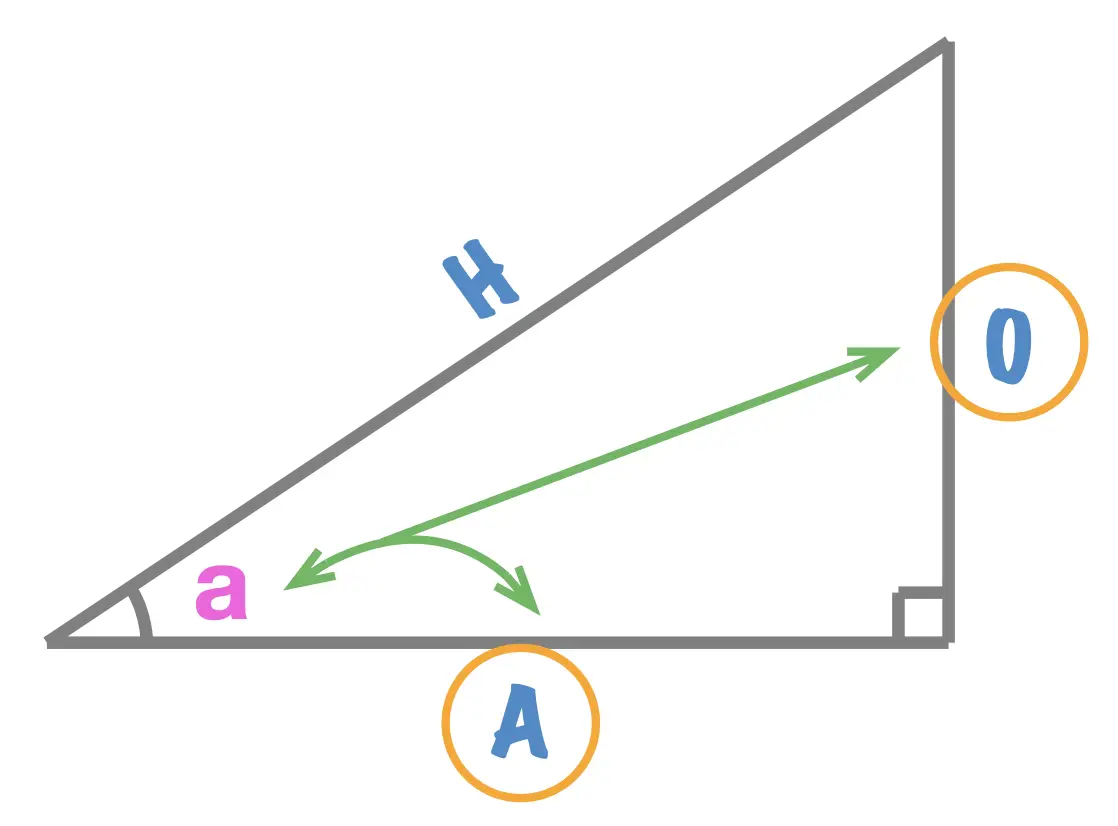
Each of the three trigonometric ratios is listed below. In each case we state the formula as well as illustrate it with two examples (one for each of the interior angles, \(a\) and \(b\), of the triangle). Make a note of each of the ratios and make sure to notice that the value of sine, cosine, tangent, depends on the interior angle that we're focusing on; we calculat the sine, cosine and tangent of an angle not of a triangle.
Tutorial: Trigonometric Ratios
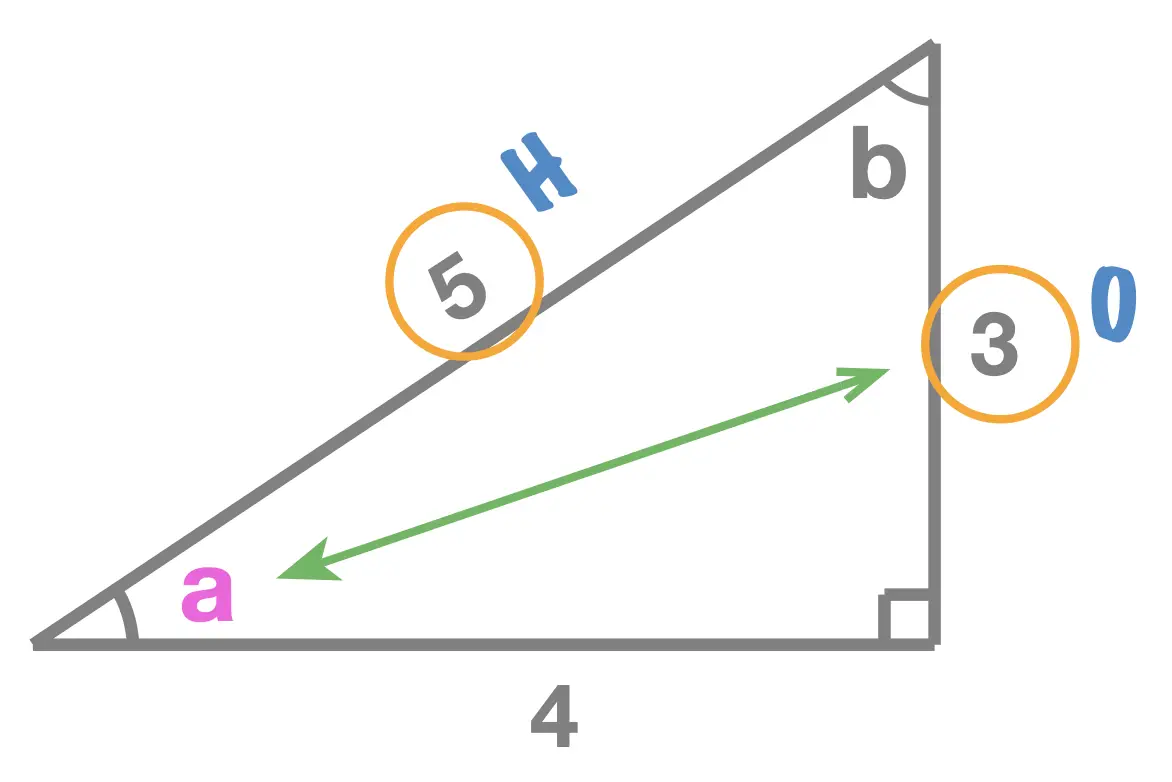
SINE = Opposite \(\div \) Hypotenuse
Given a right angle triangle and one of its interior angles \(a\), the sine of angle \(a\) equals to:
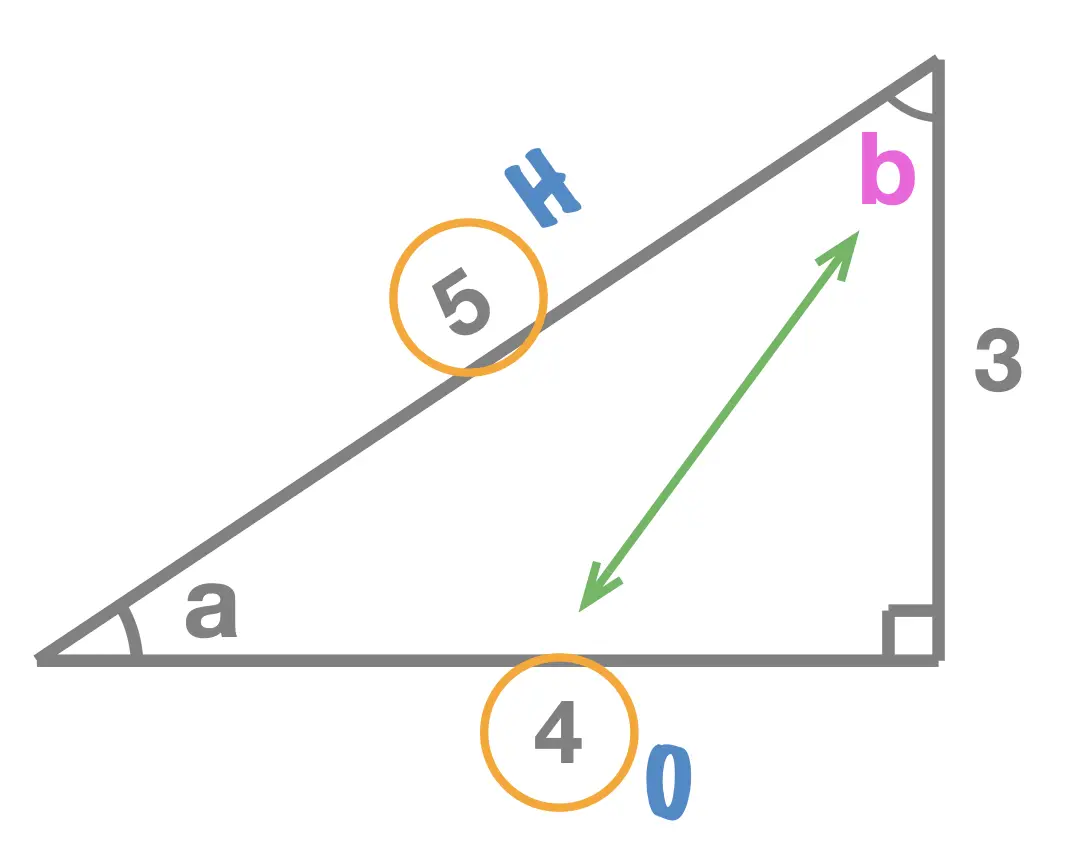
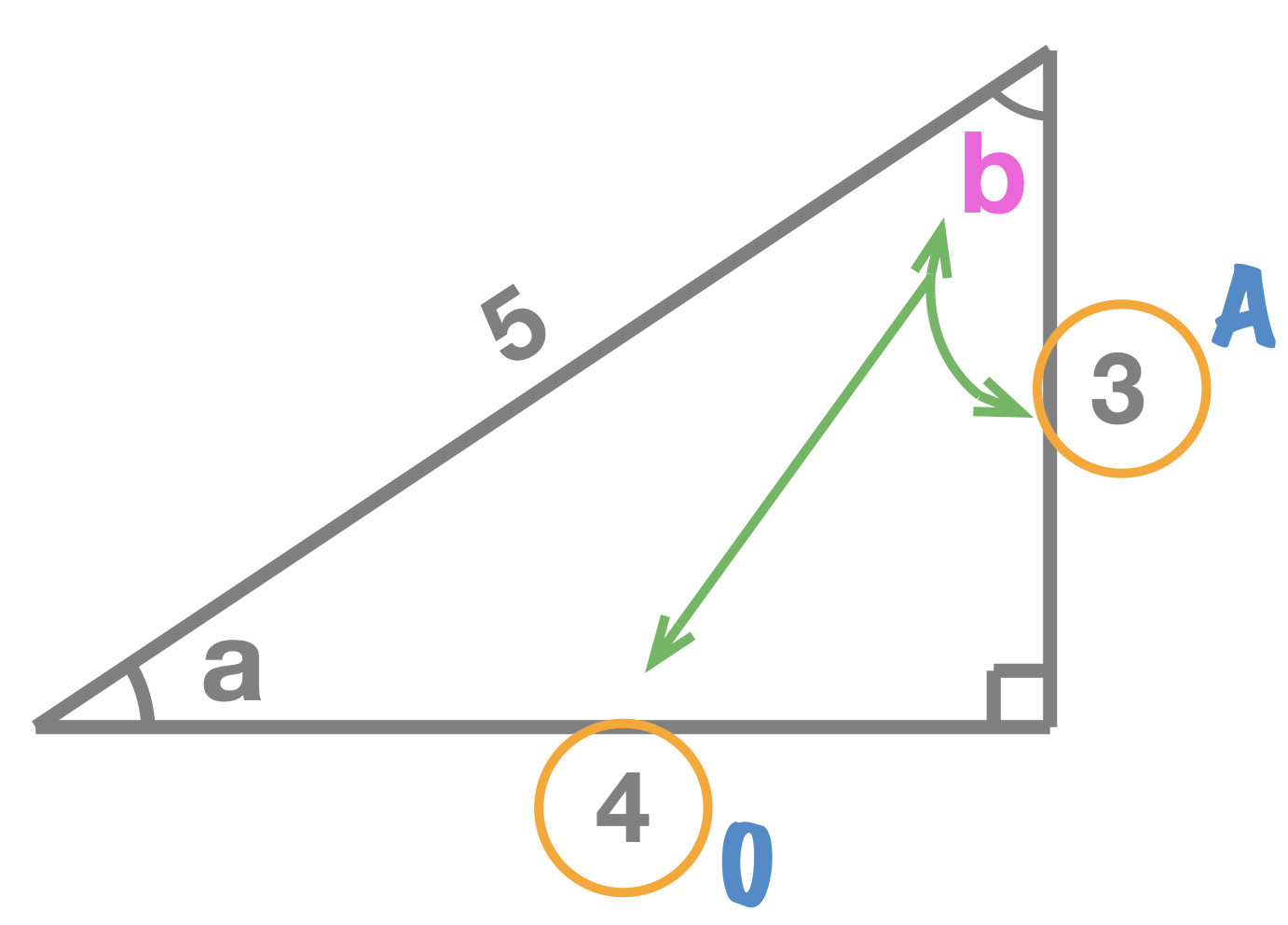
COSINE = Adjacent \(\div \) Hypotenuse
Given a right angle triangle and one of its interior angles \(a\), the sine of angle \(a\) equals to:
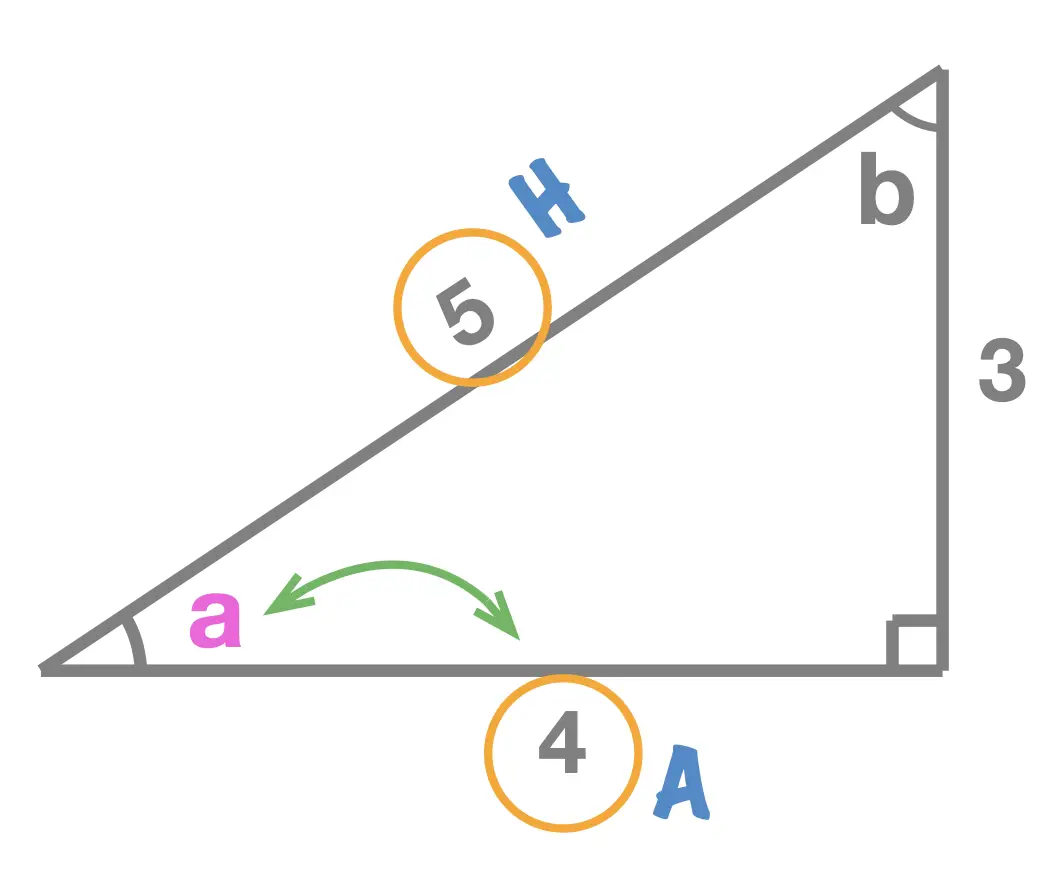
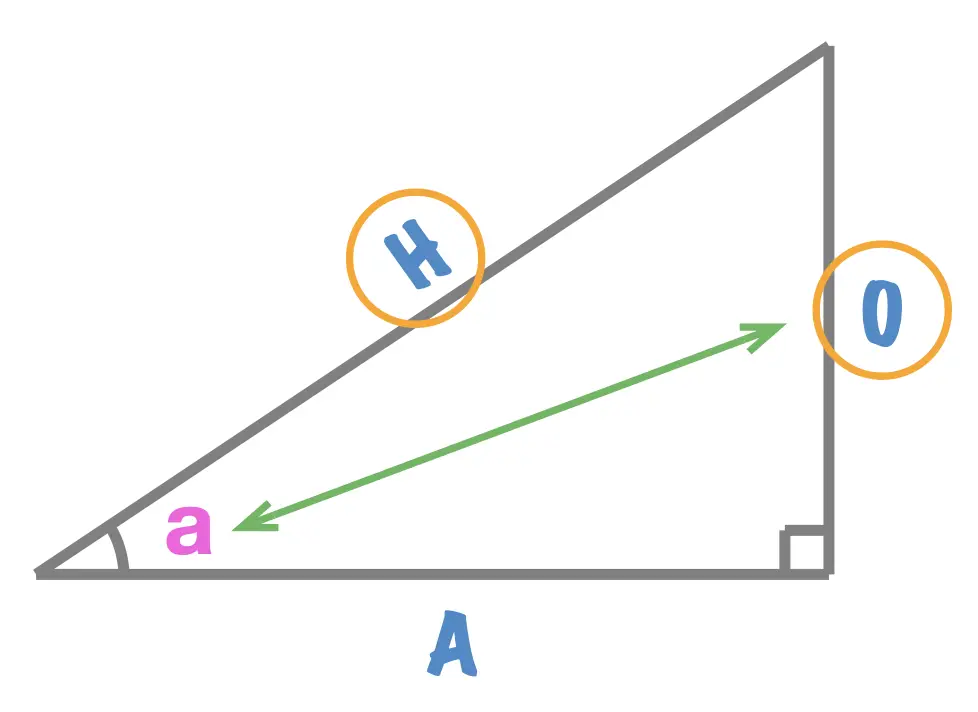
TANGENT = Opposite \(\div \) Adjacent
Given a right angle triangle and one of its interior angles \(a\), the tangent of angle \(a\), written \(tan(a)\), equals to:
Exercise 1
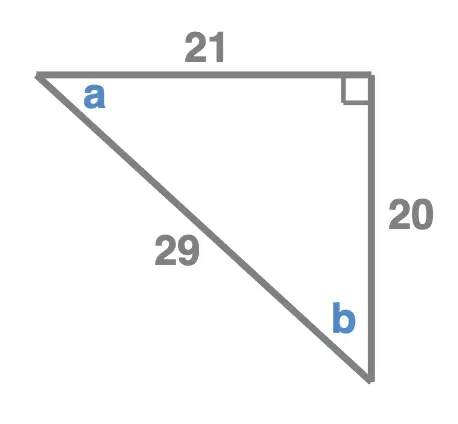
For each of the right angle triangles, below, calculate:
-
- \(sin(a)\)
- \(cos(a)\)
- \(tan(a)\)
-
- \(sin(b)\)
- \(cos(b)\)
- \(tan(b)\)
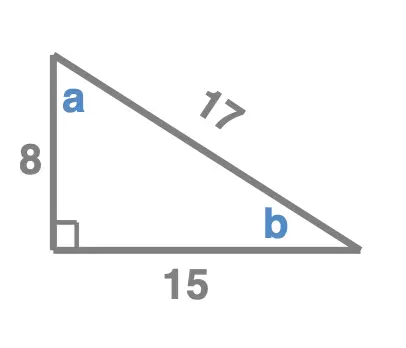
Triangle 1
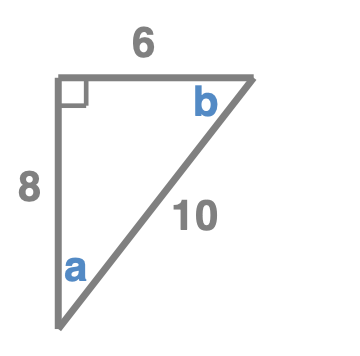
Triangle 2
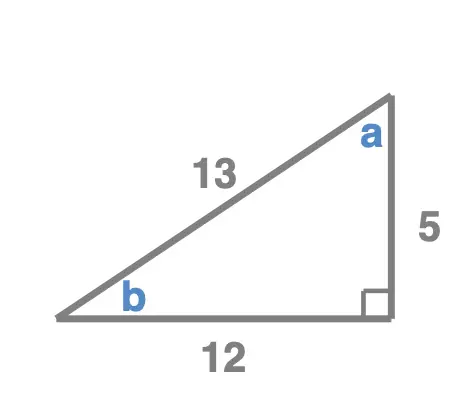
Triangle 3
Triangle 4
Solution Without Working
Triangle 1
-
- \(sin(a) = 0.882\)
- \(cos(a) = 0.471\)
- \(tan(a) = 1.88\)
-
- \(sin(b) = 0.471\)
- \(cos(b) = 0.882\)
- \(tan(b) = 0.533\)
Triangle 2
-
- \(sin(a) = 0.6\)
- \(cos(a) = 0.8\)
- \(tan(a) = 0.75\)
-
- \(sin(b) = 0.8\)
- \(cos(b) = 0.6\)
- \(tan(b) = 1.33\)
Triangle 3
-
- \(sin(a) = 0.923\)
- \(cos(a) = 0.385\)
- \(tan(a) = 2.4\)
-
- \(sin(b) = 0.385\)
- \(cos(b) = 0.923\)
- \(tan(b) = 0.417\)
Triangle 4
-
- \(sin(a) = 0.690\)
- \(cos(a) = 0.724\)
- \(tan(a) = 0.952\)
-
- \(sin(b) = 0.724\)
- \(cos(b) = 0.690\)
- \(tan(b) = 1.05\)
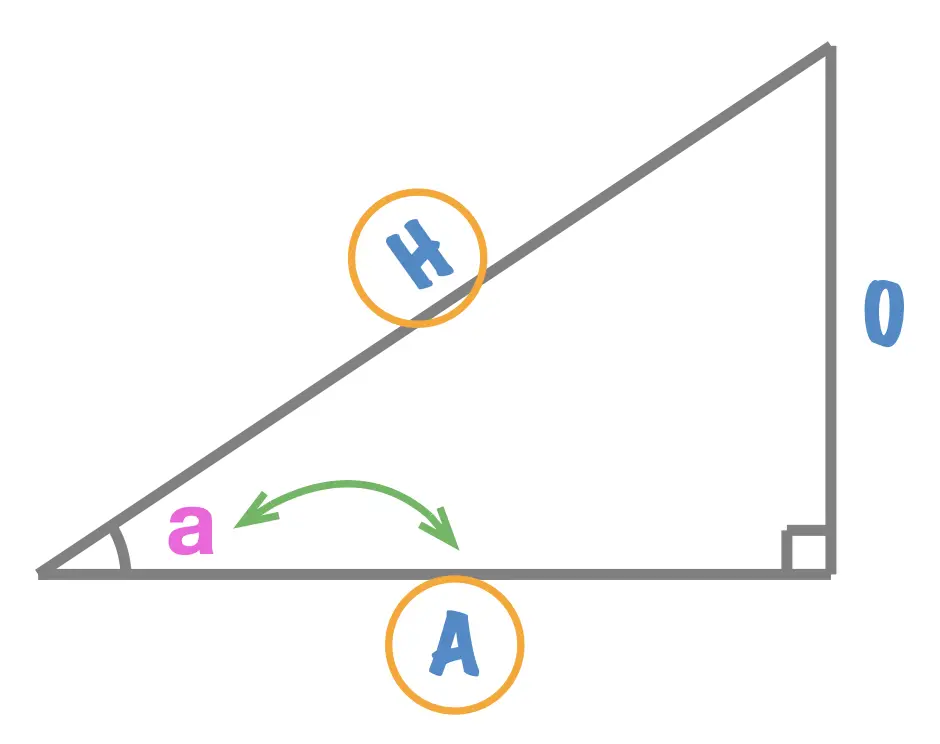
SOH CAH TOA
SOH CAH TOA is an acronym used to memorize the three trigonometric ratios.
Indeed simply say "SOH CAH TOA" a few times and you'll remember those "words".
Watch the following Tutorial to learn how to use it.
Tutorial: Using SOH-CAH-TOA
In the following tutorial we learn how to use SOH-CAH-TOA to find trigonometric ratios.
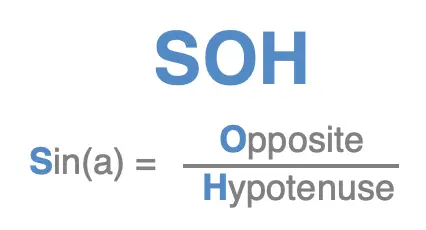
SOH
SOH gives us the first letter of each of words we need to know to remember the trigonometric ratio for the sine of an angle \(a\):
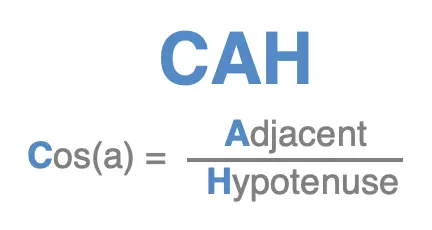
CAH
CAH gives us the first letter of each of words we need to know to remember the trigonometric ratio for the cosine of an angle \(a\):
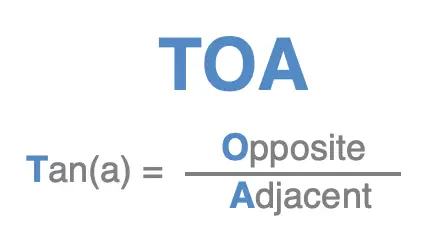
TOA
TOA gives us the first letter of each of words we need to know to remember the trigonometric ratio for the tangent of an angle \(a\):
Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.