RadfordMathematics.com

Binomial Distribution - Cumulative Distribution Function (CDF)

Given a discrete random variable \(X\), that follows a binomial distribution, its binomial cumulative distribution function, allows us to calculate the probability that the number of successes be less than, or equal to, a given value. That is it allows us to calculate: \[P\begin{pmatrix} X \leq k \end{pmatrix}, \quad 0 \leq k \leq n\]

Binomial Cumlative Distribution Function (CDF)

Given a discrete random variable \(X\) that follows a binomial distribution, the probability of \(r\) successes within \(n\) trials is given by: \[P\begin{pmatrix}X \leq k \end{pmatrix} = \sum_{r=0}^k P \begin{pmatrix} X = r \end{pmatrix}\] So that's: \[P\begin{pmatrix}X \leq k \end{pmatrix} = P \begin{pmatrix} X = 0 \end{pmatrix} + P \begin{pmatrix} X = 1 \end{pmatrix} + \dots + P \begin{pmatrix} X = k \end{pmatrix}\]

Typical Question

A biased coin has probability of flipping heads \(p=0.6\). The coin is flipped \(20\) times. What is the probability of flipping 4 heads or less ?

Comment

Define the discrete random variable \(X\) as "\(X\): the number of times we flip heads", it is clear that \(X\) follows a binomial distribution with \(20\) trials and a probability of success \(p=0.6\). Using the notation we saw in the previous section, we can therefore write \(X \sim B \begin{pmatrix}20,0.6 \end{pmatrix}\).

The probability of flipping 4 heads or less is therefore: \[P\begin{pmatrix} X \leq 4 \end{pmatrix}\] This is unlike what we saw in the previous section where we learnt how to calculate the probability that \(X\) take-on a specific value, \(P\begin{pmatrix}X = k\end{pmatrix}\). Instead we're now interested in learning how to calculate the probability that \(X\) be less than, or equal to, a specific value \(P\begin{pmatrix}X \leq k \end{pmatrix}\).

To calculate such probabilities we use the Cumulative Distribution Function, CDF defined next.

Binomial CDF on the Calculator

Most graphical calculators have the binomial cumulative distribution function, binomial CDF, preprogrammed.

  • Texas Intristruments calculators name this function binomCdf
  • Casio calculators name this function binomialCD

Here's how to reach the Binomial CDF function on 3 well-known calculators:

TI 84

From basic Calculator Press:
  • 2ND
  • VARS (to reach DISTR)
  • binomcdf

CASIO 35+

From Calculator Page, Press:
  • OPTN
  • STAT (F5)
  • DIST (F3)
  • BINM (F5)
  • Bcd (F2)

TI Nspire CX

From ScratchPad, Press:
  • Menu
  • Probability
  • Distributions
  • Binomial CDF
Say, for example, we were dealing with a discrete random variable \(X\) that follows a binomial distribution in 8 trials and a probability of a success, \(p=0.4\) and that we wanted to calculate \(p\begin{pmatrix}X\leq 3\end{pmatrix}\), then here's what we would type for each of these calculators:

TI 84

Input

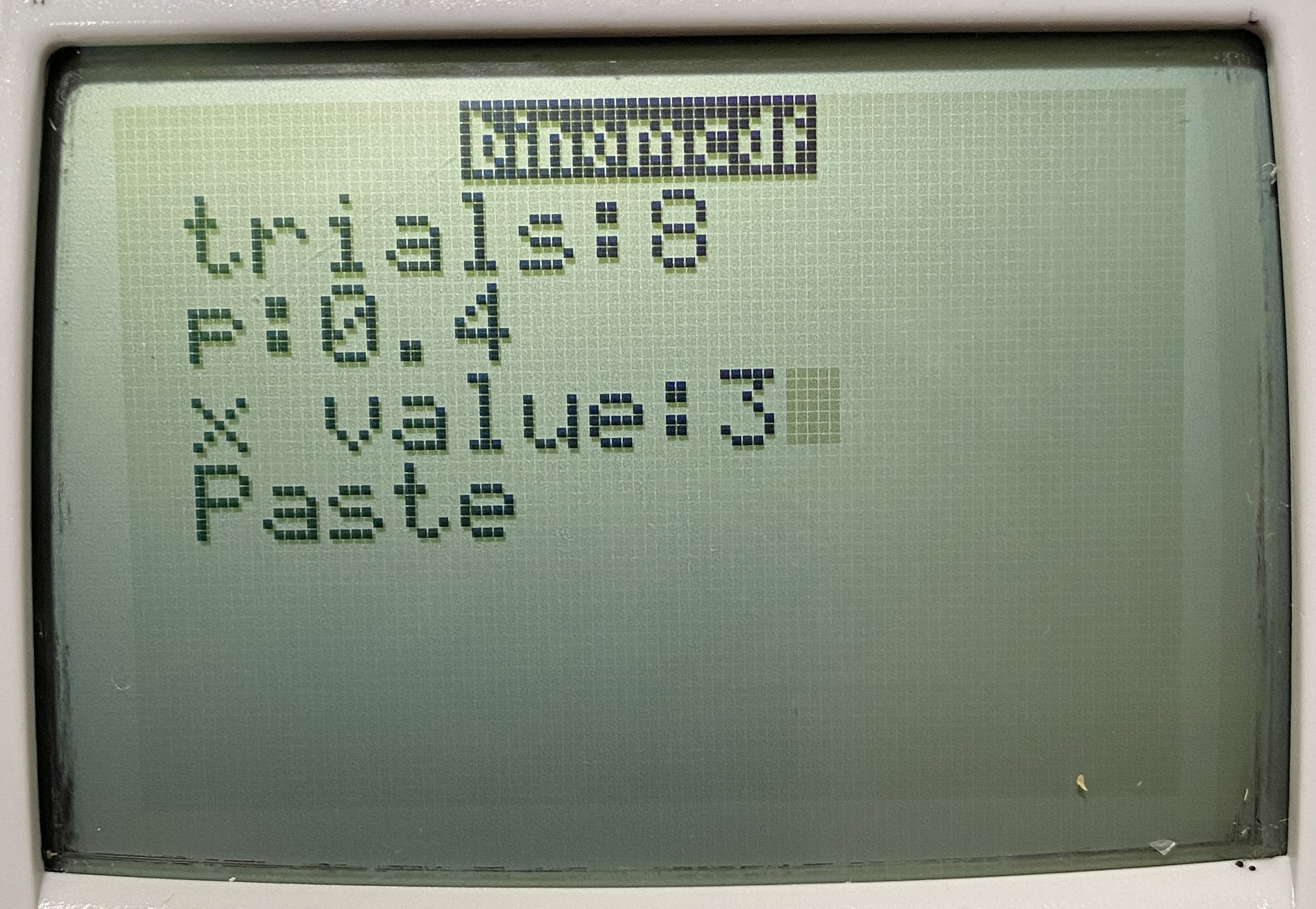
Output

CASIO 35+

Input

Output

TI Nspire CX

Input

Output

In all 3 cases, we find that \(p\begin{pmatrix}X\leq 3 \end{pmatrix} = 0.594\).

Notice that:

  • The CASIO 35+ requires us to know which order to enter the input values. Ineed we have to type (in order): the upper bound (3), the number of trials (8) and the probability of a success (0.4), separated by a comma.
  • The TI Nspire CX asks us to specify a lower bound, where as the other calculators only take an upper bound as an input. This will be a real avantage when we have to calculate probabilities of the type \(p\begin{pmatrix}a\leq X \leq b\end{pmatrix}\) or \(p\begin{pmatrix}X\geq k \end{pmatrix}\) as we'll see further down.

Binomial CDF : Lesson & Examples

In this tutorial we consider a continuous random variable that follows a normal distribution with mean \(\mu = 88\) and standard deviation \(\sigma = 19\).

Worked Example 1

A bag contains \(10\) marbles, \(6\) of which are blue and \(4\) are red. An experiment consists of picking a marble (at random) from the bag, making a note of its color and putting it back in the bag. This experiment is repeated \(5\) times.

What is the probability of picking \(3\) blue marbles or less?

Solution

We define the discrete random variable \(X\) as the "number of blue marbles picked". Since each trial is independent from the previous (the marble is replaced each time) we can say that \(X\) follows a binomial distribution, with parameters \(n=5\) and \(p=0.6\) (the probability of picking a blue marble). Or using the notation we learnt in the previous section we can write \(X\sim B \begin{pmatrix}5,0.6 \end{pmatrix}\).

Now, using the binomial cumulative probability distribution function with \(5\) trials, \(n = 5\), probability of a success \(p = 0.6\), for \(3\) successes, \(r = 3\), we find: \[\begin{aligned} P\begin{pmatrix} X \leq 3 \end{pmatrix} & = \sum_{r=0}^k P \begin{pmatrix} X = r \end{pmatrix} \\ & \text{that's:} \\ P\begin{pmatrix} X \leq 3 \end{pmatrix} &= P\begin{pmatrix} X = 0 \end{pmatrix} + P\begin{pmatrix} X = 1 \end{pmatrix} + P\begin{pmatrix} X = 2 \end{pmatrix} + P\begin{pmatrix} X = 3 \end{pmatrix} \end{aligned}\] To calculate each of the probabilities, \(P\begin{pmatrix}X = 0 \end{pmatrix}\), \(P\begin{pmatrix}X = 1 \end{pmatrix}\), ... we could use the binomial probability distribution function we learned in the previous section, which would mean calculating: \[P\begin{pmatrix} X \leq 3 \end{pmatrix} = \begin{pmatrix}5 \\ 0 \end{pmatrix}(0.6)^0\times (0.4)^5 + \begin{pmatrix}5 \\ 1 \end{pmatrix}(0.6)^1\times (0.4)^4 + \begin{pmatrix}5 \\ 2 \end{pmatrix}(0.6)^2\times (0.4)^3 + \begin{pmatrix}5 \\ 3 \end{pmatrix}(0.6)^3\times 0.4^2\] and would lead to: \[P \begin{pmatrix} X \leq 3 \end{pmatrix} = 0.66304\] But this would be a lot of work! Instead we use our calculator and the built-in binomial cdf function. This allows to simply write: \[\begin{aligned} p\begin{pmatrix}X\leq 3\end{pmatrix} & = \text{binomCdf}\begin{pmatrix}5,0.5,3\end{pmatrix} \\ & = 0.66304 \end{aligned}\]

Alongside having to calculate probabilities of the type \(p\begin{pmatrix}X\leq k \end{pmatrix}\), we'll often have to calculate the probability that \(X\) lie between 2 values, or that it be greater than a given value. For such probabilities we'll need the following important results.

Important Results

  1. To calculate \(p \begin{pmatrix} X < k \end{pmatrix}\), we use the following result: \[p\begin{pmatrix} X < k \end{pmatrix} = p\begin{pmatrix} X \leq k-1 \end{pmatrix}\]
  2. To calculate \(p\begin{pmatrix}a < X \leq b\end{pmatrix}\) and \(p\begin{pmatrix}a \leq X \leq b \end{pmatrix}\), we use: \[p\begin{pmatrix}a < X \leq b\end{pmatrix} = p\begin{pmatrix}X \leq b \end{pmatrix}-p\begin{pmatrix}X\leq a \end{pmatrix}\] and \[p\begin{pmatrix}a \leq X \leq b\end{pmatrix} = p\begin{pmatrix}X \leq b \end{pmatrix}-p\begin{pmatrix}X\leq a - 1 \end{pmatrix}\]
  3. To calculate \(p\begin{pmatrix}X \geq k \end{pmatrix}\) or \(p\begin{pmatrix}X > k \end{pmatrix}\), we use the following results: \[p\begin{pmatrix}X > k \end{pmatrix} = 1 - p\begin{pmatrix}X\leq k \end{pmatrix}\]
    and
    \[\begin{aligned} p\begin{pmatrix}X\geq k \end{pmatrix} & = 1 - p\begin{pmatrix}X < k \end{pmatrix}, \text{ and so:}\\ p\begin{pmatrix}X\geq k \end{pmatrix} & = 1 - p\begin{pmatrix}X\leq k-1 \end{pmatrix} \end{aligned}\]

Important to Know

  • In the 3rd result, for \(p\begin{pmatrix}X\geq k \end{pmatrix}\) and \(p\begin{pmatrix}X > k \end{pmatrix}\), we have to make use of the complement event. To read more about how this works, click HERE
  • If your calculator lets you enter a lower bound for the built-in Binomial CDF function then you won't have to use the complement event since you'll be able to calculate \(p\begin{pmatrix}X\geq k\end{pmatrix}\) and \(p\begin{pmatrix}a \leq X \leq b \end{pmatrix}\) directly.

    For example, if \(X\sim B\begin{pmatrix}8,0.) with the TI Nspire CX, to find \(p\begin{pmatrix}X\geq 3\end{pmatrix}\) and \(p\begin{pmatrix} 2 \leq X \leq 4\end{pmatrix}\)

Worked Example 2

A biased coin is such that the probability of flipping heads is \(p=0.7\). The coin is flipped \(20\) times. What is the probability of getting:

  1. Less than 12 heads?
  2. Anything from 12 to 14 heads?
  3. At least 8 heads?
flipping at least \(8\) heads?

Solution

We start by defining the discrete random variable \(X\) as "the number of heads obtained in \(20\) trials". Since each flip is independent from the previous it is clear that \(X\) follows a binomial distribution with parameters \(n = 20\) and \(p=0.7\) (the probability of a "success", flipping heads, for each trial). So we can write \(X\sim B\begin{pmatrix}20,0.7\end{pmatrix}\).

  1. Using the 1st important result (stated further-up), we can state: \[\begin{aligned} p\begin{pmatrix}X < 12 \end{pmatrix} & = p\begin{pmatrix} X \leq 11 \end{pmatrix} \\ & = p\begin{pmatrix} X = 0 \end{pmatrix} + \dots + p\begin{pmatrix} X = 11 \end{pmatrix} \\ & = \text{binomCdf}\begin{pmatrix}20,0.7,11 \end{pmatrix} \\ p\begin{pmatrix}X < 12 \end{pmatrix} & = 0.113 \end{aligned}\]
  2. Using the 2nd important result, we can state: \[\begin{aligned} p\begin{pmatrix}12 \leq X \leq 14 \end{pmatrix} & = p\begin{pmatrix} X = 12 \end{pmatrix} + \dots + p\begin{pmatrix} X = 14 \end{pmatrix} \\ & = p\begin{pmatrix} X \leq 14 \end{pmatrix} - p\begin{pmatrix} X \leq 11 \end{pmatrix} \\ & = \text{binomCdf}\begin{pmatrix}20,0.7,14\end{pmatrix} - \text{binomCdf}\begin{pmatrix}20,0.7,11\end{pmatrix} \\ p\begin{pmatrix}12 \leq X \leq 14 \end{pmatrix} & = 0.470 \end{aligned}\]
  3. Using the 3rd important result: \[\begin{aligned} p\begin{pmatrix} X \geq 8 \end{pmatrix} & = 1 - p\begin{pmatrix}X < 8 \end{pmatrix} \\ & = 1 - p\begin{pmatrix} X \leq 7 \end{pmatrix} \\ & = 1 - \begin{pmatrix} p\begin{pmatrix}X = 0 \end{pmatrix} + \dots + p\begin{pmatrix} X = 7 \end{pmatrix} \end{pmatrix} \\ & = 1 - \text{binomCdf}\begin{pmatrix}20,0.7,7\end{pmatrix} \\ & = 0.999 \end{aligned}\]

Exercise 1

A discrete random variable \(X\) follows a binomial distribution such that \(X\sim B\begin{pmatrix}10,0.2\end{pmatrix}\). Find each of the following probabilities:

  1. \(P\begin{pmatrix}X \leq 4\end{pmatrix}\)
  2. \(P\begin{pmatrix}X < 3\end{pmatrix}\)
  3. \(P\begin{pmatrix}2\leq X \leq 5\end{pmatrix}\)
  4. \(P\begin{pmatrix}2 < X < 5\end{pmatrix}\)
  1. \(P\begin{pmatrix}2 < X \leq 5\end{pmatrix}\)
  2. \(P\begin{pmatrix}2\leq X < 5\end{pmatrix}\)
  3. \(P\begin{pmatrix}X \geq 6\end{pmatrix}\)
  4. \(P\begin{pmatrix}X > 4\end{pmatrix}\)

Exercise 2

  1. Charlotte and Clara are planning a 7 day trip to Falkenberg, Sweden. The probability that it rains on any one of those days is 0.3. Find the probability that:
    1. it rains 3 days or less
    2. it rains less than 3 days
    3. it rains 5 days or more
    4. it rains between 3 and 5 days included
    5. it rains 3 or 5 days.
  2. 8 students sit a highly advanced mathematics test. The probability that a student scores above 80% is 0.1. Find the the probability that:
    1. no more than 2 students score above 80%
    2. at least 1 student scores above 80%
    3. 2 to 4 students, included, score more than 80%.
    4. less than 4 students score more than 80%.
  3. The process with which a famous smartphone company has its phones manufactured is such such that the probability of a phone being faulty is 0.03. In an hour 100 phones are manufactured. Find the probability that:
    1. 5 phones, or less, are faulty
    2. 2 phones or more are faulty
    3. at least 1 phone is faulty.
    4. 3 to 6 phones are faulty


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.