Discrete Random Variables & Probability Distribution Functions (PDF)
In this section we learn about discrete random variables and probability distribution functions, which allow us to calculate the probabilities associated to a discrete random variable.
We start by defining discrete random variables and then define their probability distribution functions (pdf) and learn how they are used to calculate probabilities.
Tutorial
In the following tutorial, we learn more about what discrete random variables and probability distribution functions are and how to use them. Watch it before carrying-on.
Definition: Discrete Random Variable
Discrete Variables
A discrete variable is a variable that can "only" take-on certain numbers on the number line.
We usually refer to discrete variables with capital letters:
\[X, \ Y, \ Z, \ \dots \]
A typical example would be a variable that can only be an integer, or a variable that can only by a positive whole number.
Discrete variables can either take-on an infinite number of values or they can be limited to a finite number of values.
For instance the number we obtain , when rolling a dice is a discrete variable, which is limited to a finite number of values:\(1, \ 2, \ 3, \ 4, \ 5, \) or \(6\).
An example of a discrete variable that can take-on an "infinite" number of values could be: the number of rain drops that fall over a square kilometer in Sweden on November 25th.
Note: although this quantity can technically not be infinite, it is common practice and acceptable to assume so.
Discrete Random Variables
A discrete variable is a discrete random variable if the sum of the probabilities of each of its possible values is equal to \(1\).
Example
When we roll a single dice, the possible outcomes are:
\[1, \ 2, \ 3, \ 4, \ 5, \ 6\]
The probability of each of these outcomes is \(\frac{1}{6}\).
If we define the discrete variable \(X\) as:
Probability Distribution Function (PDF)
Given a discrete random variable, \(X\), its probability distribution function, \(f(x)\), is a function that allows us to calculate the probability that \(X=x\).
In other words, \(f(x)\) is a probability calculator with which we can calculate the probability of each possible outcome (value) of \(X\).
\[P\begin{pmatrix}X = x \end{pmatrix} = f(x) \]
Example
A bag contains several balls numbered either: \(2\), \(4\) or \(6\) with only one number on each ball. A simple experiment consists of picking a ball, at random, out of the bag and looking at the number written on the ball.
Defining the discrete random variable \(X\) as:
- State the possible values that \(X\) can take.
- Calculate the probability of picking a ball with \(2\) on it.
- Calculate the probability of picking a ball with \(4\) on it.
Distribution Tables & Graphs
To illustrate the probabilities of each of the possible values a discrete random variable \(X\) can take, it will often be useful to showcase all the possible values of \(X\) alongside the corresponding probability.
This is usually done in either:
- a probability distribution table, or
- a bar chart.
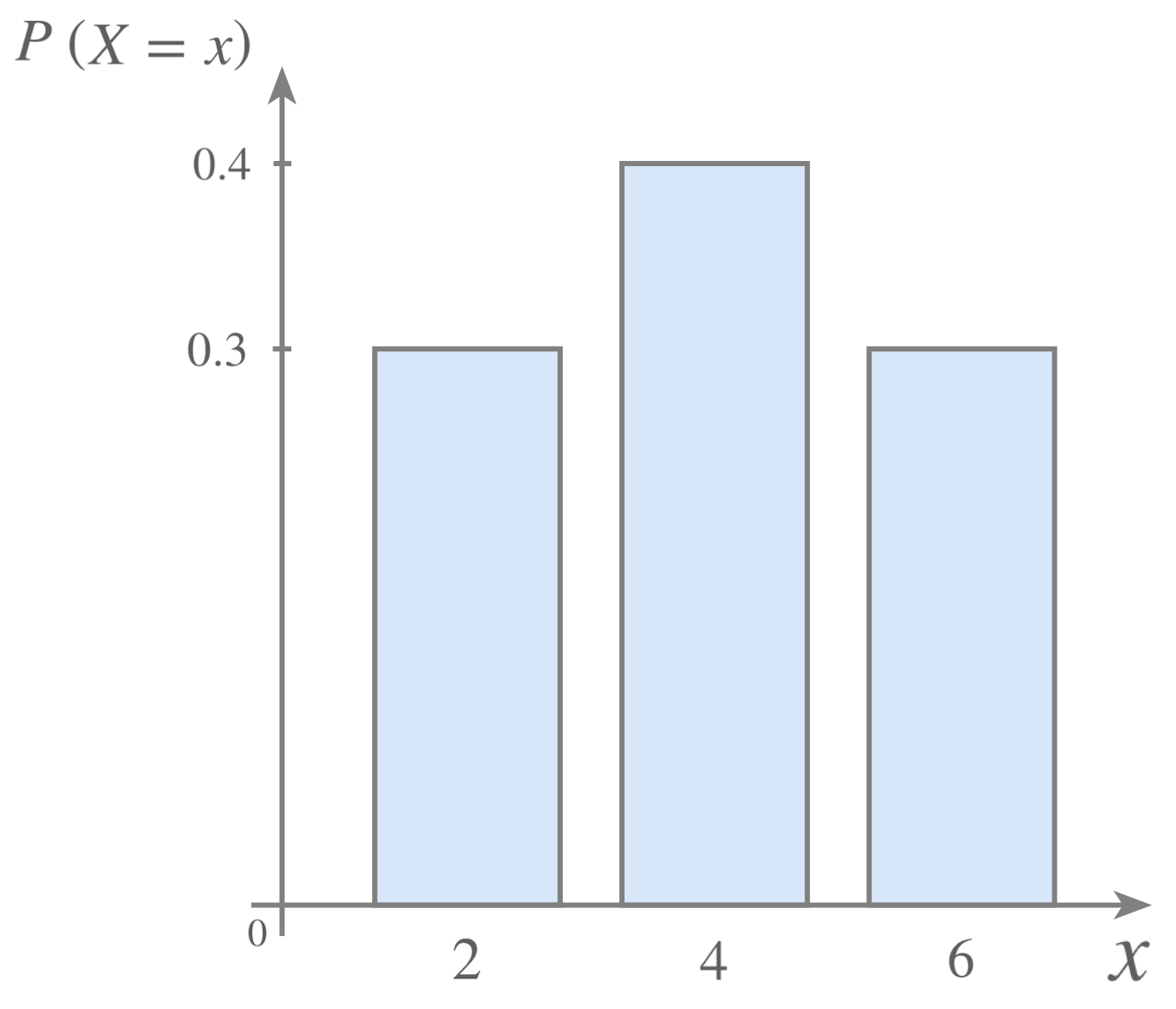
Example: Distribution Table & Graph
We'll stick to the example we saw further up:
A game of chance consists of picking, at random, a ball from a bag. Each ball is numbered either \(2\), \(4\) or \(6\). The discrete random variable is defined as:
The probability distribution function associated to the discrete random variable is: \[P\begin{pmatrix} X = x \end{pmatrix} = \frac{8x-x^2}{40}\]
- Construct a probability distribution table to illustrate this distribution.
- Draw a bar chart to illustrate this probability distribution.
- Use the distribution table and bar chart to determine which value the discrete random variable \(X\) is most likely to take.
Tutorial
In the following tutorial we learn how to construct probability distributions tables and their corresponding bar charts. Make sure to watch before working through the exercises below.
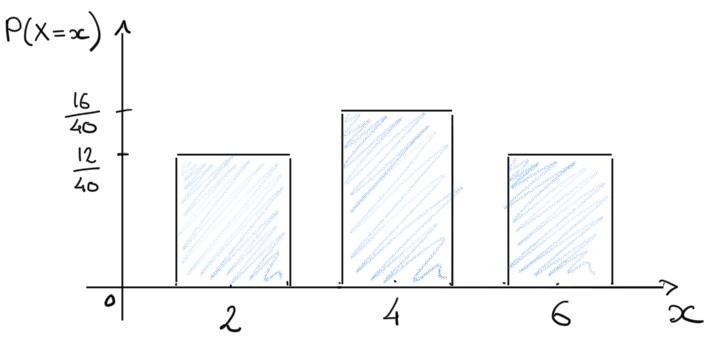
Exercise
A discrete random variable \(X\) can take either of the values: \[x = \left \{ 2, \ 4, \ 6 \right \}\] and has a probability distribution function (pdf) defined as: \[P\begin{pmatrix} X = x \end{pmatrix} = \frac{8x-x^2}{40}\]
- Construct a probability distribution table for \(X\).
- Illustrate this probability distribution with a bar chart.
- Using your previous answers, state which value the discrete random variable \(X\) most likely to take?
-
A discrete random variable \(X\) has a probability distribution function defined as:
\[P\begin{pmatrix} X = x \end{pmatrix} = kx^2\]
where: \(x = \left \{ 0, \ 1, \ 2, \ 3\right \}\).
- Find the value of \(k\).
- Calculate the probability that \(X = 2\).
-
A discrete random variable \(X\) has a probability distribution function defined as:
\[P \begin{pmatrix} X = x \end{pmatrix} = \frac{x}{k} \]
where: \(x = \left \{ 1, \ 2, \ 3, \ 4, \ 5 \right \}\).
- Find the value of \(k\).
- Illustrate this discrete probability distribution in a table.
-
A discrete random variable has a probability distribution function \(f(x)\), its distribution is shown in the following table:

- Find the value of \(k\) and draw the corresponding distribution table.
- Represent this distribution in a bar chart.
- Which value is the discrete random variable most likely to take?
Answers Without Working
-
- \(k = \frac{1}{14}\)
- \(P \begin{pmatrix} X = 2 \end{pmatrix} = \frac{2}{7}\) that's \(0.286\) (rounded to 3 significant figures).
-
- \(k = 15\)
-

-
-
\(k=-0.1\)
The probability distribution therefore becomes:

-
The graphical representation, of this distribution, is shown in the following bar chart:
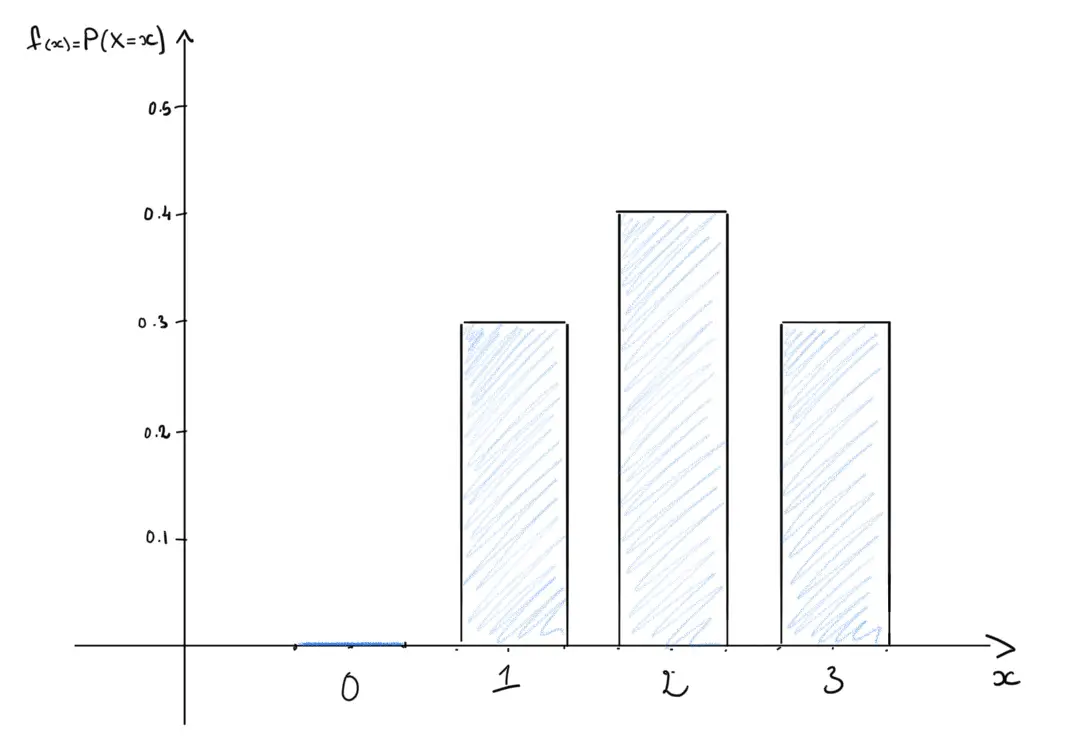
- The discrete random variable is most likely to take the value \(2\).
-
\(k=-0.1\)
Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.