Probability of A and B for Independent Events

(Combined Events Part 1)

In this section we learn how to calculate the probability of \(A\) and \(B\) occuring, that's when both events \(A\) and \(B\) happen at the same time and we learn the formula for independent events \(A\) and \(B\). Although we sometimes refer to this probability with the notation \(p\begin{pmatrix}A \ \text{and} \ B \end{pmatrix}\) we'll use the correct mathematical notation and write: \[p\begin{pmatrix}A \cap B \end{pmatrix}\] To be clear, \(p\begin{pmatrix}A \cap B \end{pmatrix}\) should be read "the probability of A and B occurring".

Venn Diagram for \(p\begin{pmatrix}A \cap B \end{pmatrix}\)

The Venn diagram shown here shows two sets \(A\) and \(B\), which correspond to two events \(A\) and \(B\). The two sets overlap, we say they intersect, thereby creating the set \(A\cap B\) (that's the event "\(A\) and \(B\)").

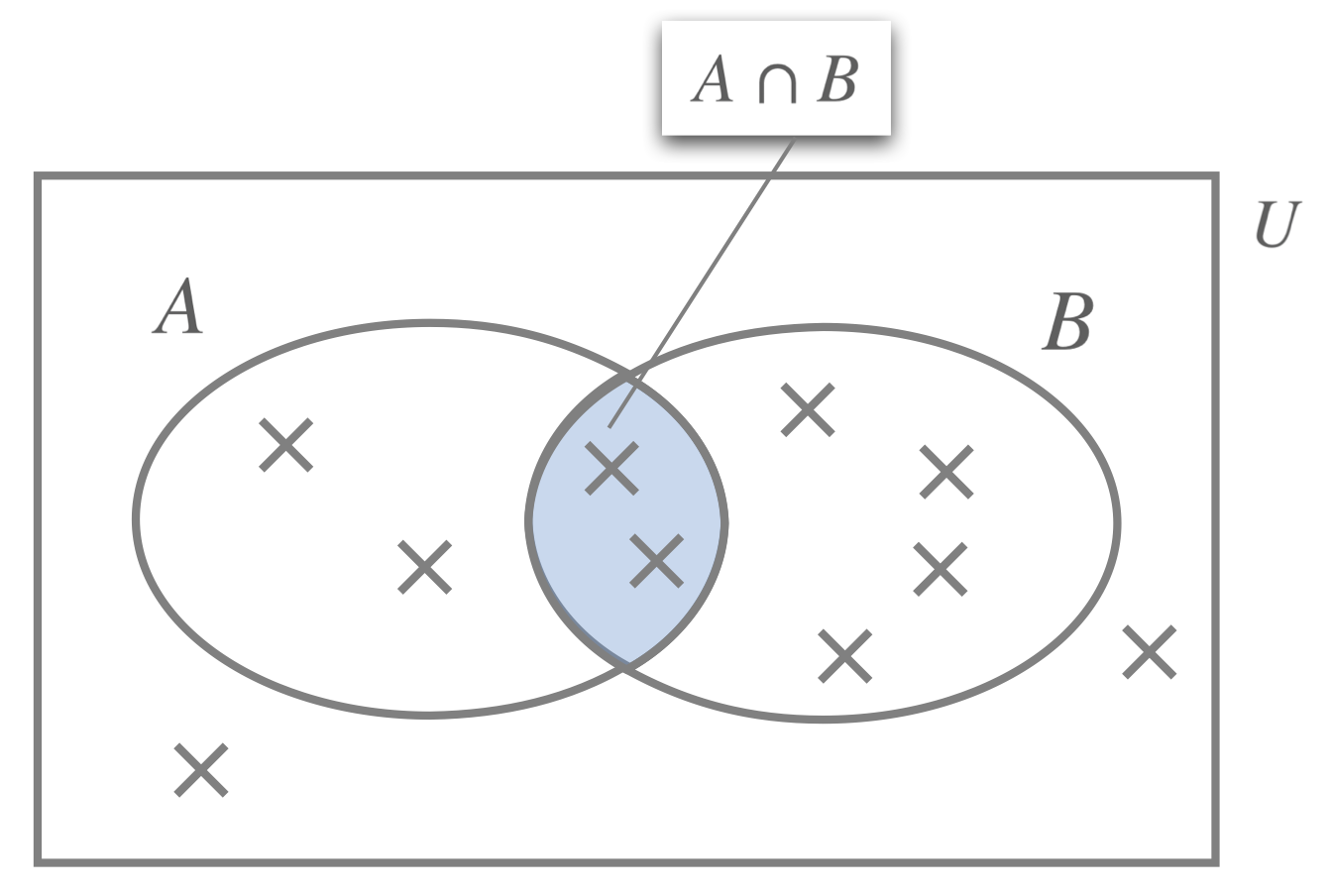
If we're given, or can find, how many elements are inside the set \(A \cap B\) and we know how many elements are inside the universal set \(U\), that's \(n\begin{pmatrix}U \end{pmatrix}\), then we can calculate \[p\begin{pmatrix}A \cap B \end{pmatrix} = \frac{n \begin{pmatrix} A \cap B \end{pmatrix}}{n \begin{pmatrix}U\end{pmatrix}}\] We frequently won't be given enough information to find both \(n\begin{pmatrix}A \cap B \end{pmatrix}\) and \(n\begin{pmatrix} U \end{pmatrix}\). Instead we'll "just" be given, or will be able to find the probabilities \(p\begin{pmatrix}A\end{pmatrix}\) and \(p\begin{pmatrix}B \end{pmatrix}\). In such cases we'll have to use the formula that we learn next.

Formula for \(p\begin{pmatrix} A \cap B\end{pmatrix}\) - Independent Events

The formula we learn here is for independent events. If you're not sure what independent events are then do make sure to click on the "Learn More" button below.

Given two events \(A\) and \(B\) that are independent, then provided we are given (or can find) the probabilities of both events, \(p\begin{pmatrix}A \end{pmatrix}\) and \(p\begin{pmatrix}B \end{pmatrix}\), we can calculate the probability \(p\begin{pmatrix}A\cap B \end{pmatrix}\) using the following formula

Formula - \(p\begin{pmatrix}A \cap B \end{pmatrix}\) for Independent Events

Given two independent events \(A\) and \(B\), the probability of the event "\(A\) and \(B\)" occurring is written \(p\begin{pmatrix}A \cap B \end{pmatrix}\) and is given by the formula: \[p\begin{pmatrix}A \cap B \end{pmatrix} = p\begin{pmatrix}A \end{pmatrix} \times p\begin{pmatrix}B \end{pmatrix}\]

Tutorial: Multiplication Rule for \(p\begin{pmatrix}A \cap B \end{pmatrix}\)

The following tutorial we see, through a couple of examples, how to use the multplcation rule for independent events.

Examples

Question: Two unbiased dice, both numbered \(1\) to \(6\), are rolled. What is the probability of rolling two \(4\)'s?

Answer: The events "rolling a 4 with the first die" and "rolling a 4 with the second die" are independent. Indeed, whatever the outcome of one die has no impact on the likelihood of rolling a 4 with the second die. We can therefore use the formula stated above to write: \[\begin{aligned} p\begin{pmatrix}\text{rolling two 4's} \end{pmatrix} & = p\begin{pmatrix} \text{rolling a 4 with one die} \end{pmatrix} \times p\begin{pmatrix} \text{rolling a 4 with the other die} \end{pmatrix} \\ & = \frac{1}{6} \times \frac{1}{6} \\ p\begin{pmatrix}\text{rolling two 4's} \end{pmatrix} & = \frac{1}{36} \end{aligned}\]

Question: A bag contains \(3\) orange marbles and \(4\) green marbles. A marble is picked at random and, once its color is noted, put bag in the bag. A second marble is then picked at random and its color noted as well. What is the probability of picking two orange marbles?
Answer: Since the first marble that is picked is put back in the back, whatever color marble is picked first will have no impact on what is picked second. The events "1st marble is orange" and "2nd marble is orange" are therefore independent and we can define those two events as:
- \(A\): picking an orange on the first draw.
- \(B\): picking an orange on the second draw.
Given there are \(3\) orange marbles and \(7\) marbles in total, we quickly see that \(p\begin{pmatrix}A\end{pmatrix} = \frac{3}{7}\) and \(p\begin{pmatrix}B\end{pmatrix} = \frac{3}{7}\). Finally, using the formula we saw further-up we can therefore calculate the probability of picking two orange marbles: \[\begin{aligned} p\begin{pmatrix}A \cap B \end{pmatrix} & = p\begin{pmatrix}A\end{pmatrix}\times p\begin{pmatrix}A\end{pmatrix} \\ & = \frac{3}{7} \times \frac{3}{7} \\ & = \frac{3\times 3}{7\times 7} \\ p\begin{pmatrix}A \cap B \end{pmatrix} & = \frac{9}{49} \end{aligned} \]

Exercise 1

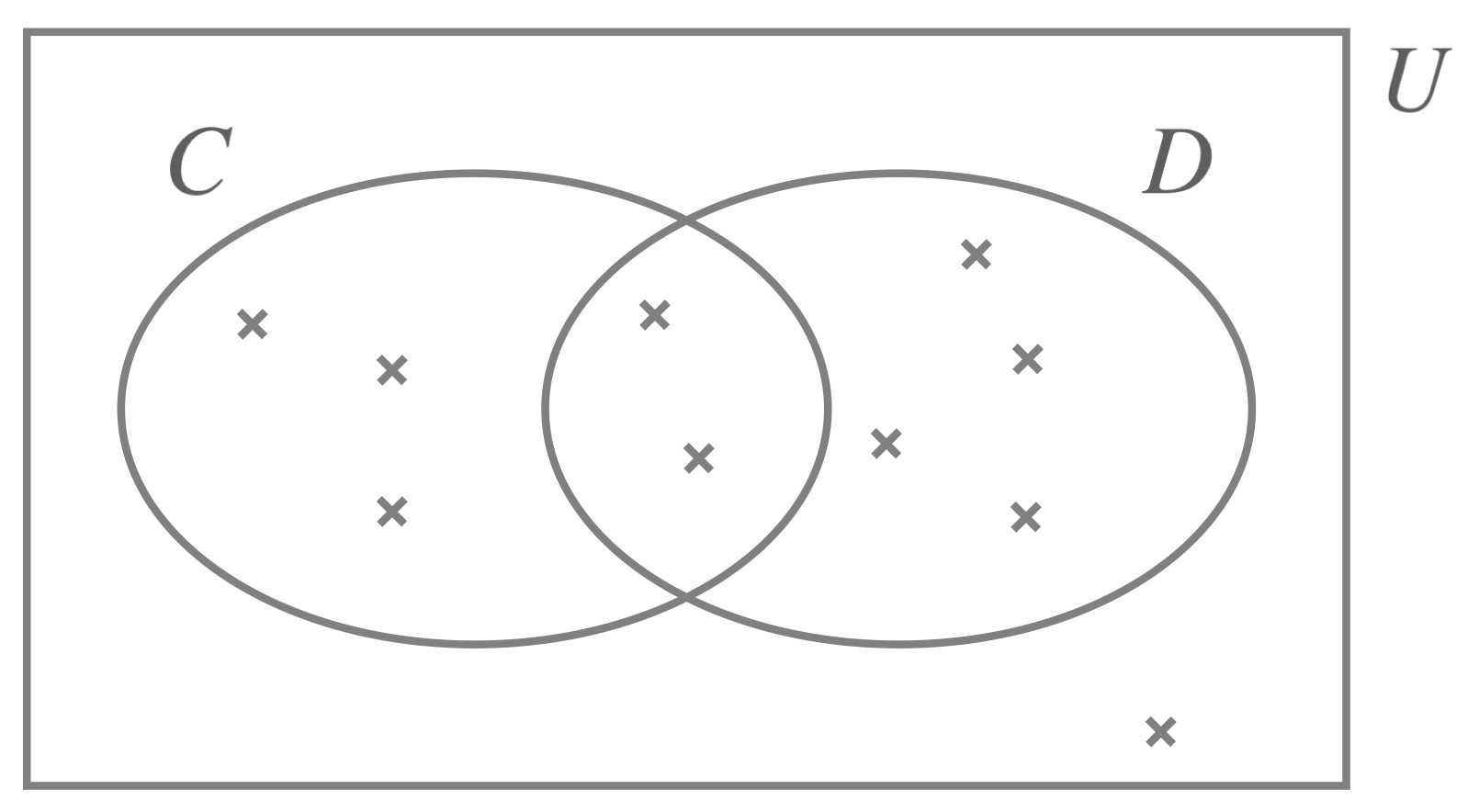
For a survey, a group of people, with pets at home, was asked whether they had a cat or a dog. The result is summarized in the Venn diagram, shown here.
1. How many people participated in the survey?
2. How many participants own a cat?
3. How many people own both a cat and a dog?
4. What is the probability that one of the people, participating in the survey, owns both a cat and a dog?

The probability that Helen do well at her Mathematics test is \(p\begin{pmatrix}M\end{pmatrix} = 0.8\). The probability that she do well at her French test is \(p\begin{pmatrix}F\end{pmatrix} = 0.7\).
1. What is the probability that Helen does well at both her Mathematics test and her French test?
2. What is the probability that Helen doesn't do well at her Mathematics test and does well at her French test?

Like every Sunday afternoon, Cathy and Jonathan play a game of darts. On any given turn, the probability that Cathy hits the center of the target is \(0.5\) and the probability that they both hit the center of the target is \(0.2\). What is the probability that Jonathan hit the center of the target?

A fair coin is tossed and an unbiased die is rolled. Find the probability of:
1. rolling an even number.
2. flipping tails.
3. rolling an even number and flipping tails.

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

1. The numbers of people who participated in the survery equals the total number of crosses we see on the Venn diagram. Since there are \(10\), we can state that the total number of outcomes equals \(10\), which we write: \[n\begin{pmatrix}U \end{pmatrix} = 10\]
2. The number of participants who own a cat is equal to the number of crosses inside the set labelled \(C\), which is \(5\). So we can write: \[n\begin{pmatrix}C \end{pmatrix} = 5\]
3. The people who own both a cat and a dog are represented by the crosses that are in both the set \(C\) and \(D\) (where the two sets overlap, we usually say where they "intersect"). We can see there are \(2\) crosses, so \(2\) people own both a cat and a dog. We write: \[n\begin{pmatrix}C \cap D \end{pmatrix} = 2\]
4. The probability that a person own both a cat and a dog is: \[\begin{aligned} p\begin{pmatrix}C \cap D \end{pmatrix} & = \frac{n \begin{pmatrix} C \cap D \end{pmatrix}}{n \begin{pmatrix}U \end{pmatrix}}\\ & = \frac{2}{10} \\ p\begin{pmatrix}C \cap D \end{pmatrix} & = 0.2 \end{aligned}\]

1. Assuming the two events \(M\) (doing well at her Math test) and \(F\) (doing well at her French test) are independent we can use the formula we saw \[\begin{aligned} p\begin{pmatrix} M \cap F \end{pmatrix} & = 0.8 \times 0.7 \\ p\begin{pmatrix} M \cap F \end{pmatrix} & = 0.56 \end{aligned}\]
2. We start by finding the probability that Helen doesn't do well at her Mathematics test. That's the complement of her doing well at her Mathematics test, so: \[\begin{aligned} p\begin{pmatrix}M'\end{pmatrix} & = 1 - p \begin{pmatrix} M \end{pmatrix} \\ & = 1 - 0.8 \\ p\begin{pmatrix}M'\end{pmatrix} & = 0.2 \end{aligned}\] We now use our formula to calculate \(p\begin{pmatrix} M' \cap F \end{pmatrix}\): \[p\begin{pmatrix} M' \cap F \end{pmatrix} = 0.2 \times 0.7 = 0.14 \]

Assuming that the two events \(C\): "Cathy hits the center of the target" and \(J\): "Jonathan hits the center of the target" are independent, we know that: \[p \begin{pmatrix} C \cap J \end{pmatrix} = p\begin{pmatrix} C \end{pmatrix} \times p\begin{pmatrix} J \end{pmatrix}\] Replacing \(p \begin{pmatrix} C \cap J \end{pmatrix}\) by \(0.2\) and \(p \begin{pmatrix} C \end{pmatrix}\) by \(0.5\) we obtain an equation for the unknown \(p \begin{pmatrix} J \end{pmatrix}\): \[0.2 = 0.5 \times p \begin{pmatrix} J \end{pmatrix}\] which leads to: \[\frac{0.2}{0.5} = p \begin{pmatrix} J \end{pmatrix}\] or \[p \begin{pmatrix} J \end{pmatrix} = \frac{0.2}{0.5} \] Finally, we find: \[p \begin{pmatrix} J \end{pmatrix} = 0.4 \]

1. We define the event \(E\): "rolling an even number" and: \[p \begin{pmatrix}E \end{pmatrix} = \frac{1}{2}\]
2. We define the event \(T\): "flipping tails" and: \[p \begin{pmatrix}T \end{pmatrix} = \frac{1}{2}\]
3. We find the probability of both rolling an even number and flipping tails, \(p\begin{pmatrix}E \cap T \end{pmatrix}\), using our formula for independent events: \[\begin{aligned} p\begin{pmatrix}E \cap T \end{pmatrix} & = p \begin{pmatrix}E \end{pmatrix} \times p\begin{pmatrix}T\end{pmatrix} \\ \frac{1}{2}\times \frac{1}{2} \\ p\begin{pmatrix}E \cap T \end{pmatrix} & = \frac{1}{4} \quad (=0.25) \end{aligned}\]

Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.

RadfordMathematics.com

Online Mathematics Book

Probability of A and B for Independent Events

(Combined Events Part 1)

Venn Diagram for \(p\begin{pmatrix}A \cap B \end{pmatrix}\)

Formula for \(p\begin{pmatrix} A \cap B\end{pmatrix}\) - Independent Events

Formula - \(p\begin{pmatrix}A \cap B \end{pmatrix}\) for Independent Events

Tutorial: Multiplication Rule for \(p\begin{pmatrix}A \cap B \end{pmatrix}\)

Examples

Exercise 1

RadfordMathematics.com

Online Mathematics Book

Probability of A and B for Independent Events

(Combined Events Part 1)

Venn Diagram for \(p\begin{pmatrix}A \cap B \end{pmatrix}\)

Formula for \(p\begin{pmatrix} A \cap B\end{pmatrix}\) - Independent Events

Independent Events, or Dependent Events?

Independent Events

Dependent Events (Conditional Probability)

Formula - \(p\begin{pmatrix}A \cap B \end{pmatrix}\) for Independent Events

Tutorial: Multiplication Rule for \(p\begin{pmatrix}A \cap B \end{pmatrix}\)

Examples

Exercise 1

Exercise 1 - Answer Key