Cross Product of Two Vectors - Multiplying Vectors
(Vector Product of Two Vectors)
The cross product, also called vector product of two vectors is written \(\vec{u}\times \vec{v}\) and is the second way to multiply two vectors together.
When we multiply two vectors using the cross product we obtain a new vector. This is unlike the scalar product (or dot product) of two vectors, for which the outcome is a scalar (a number, not a vector!).
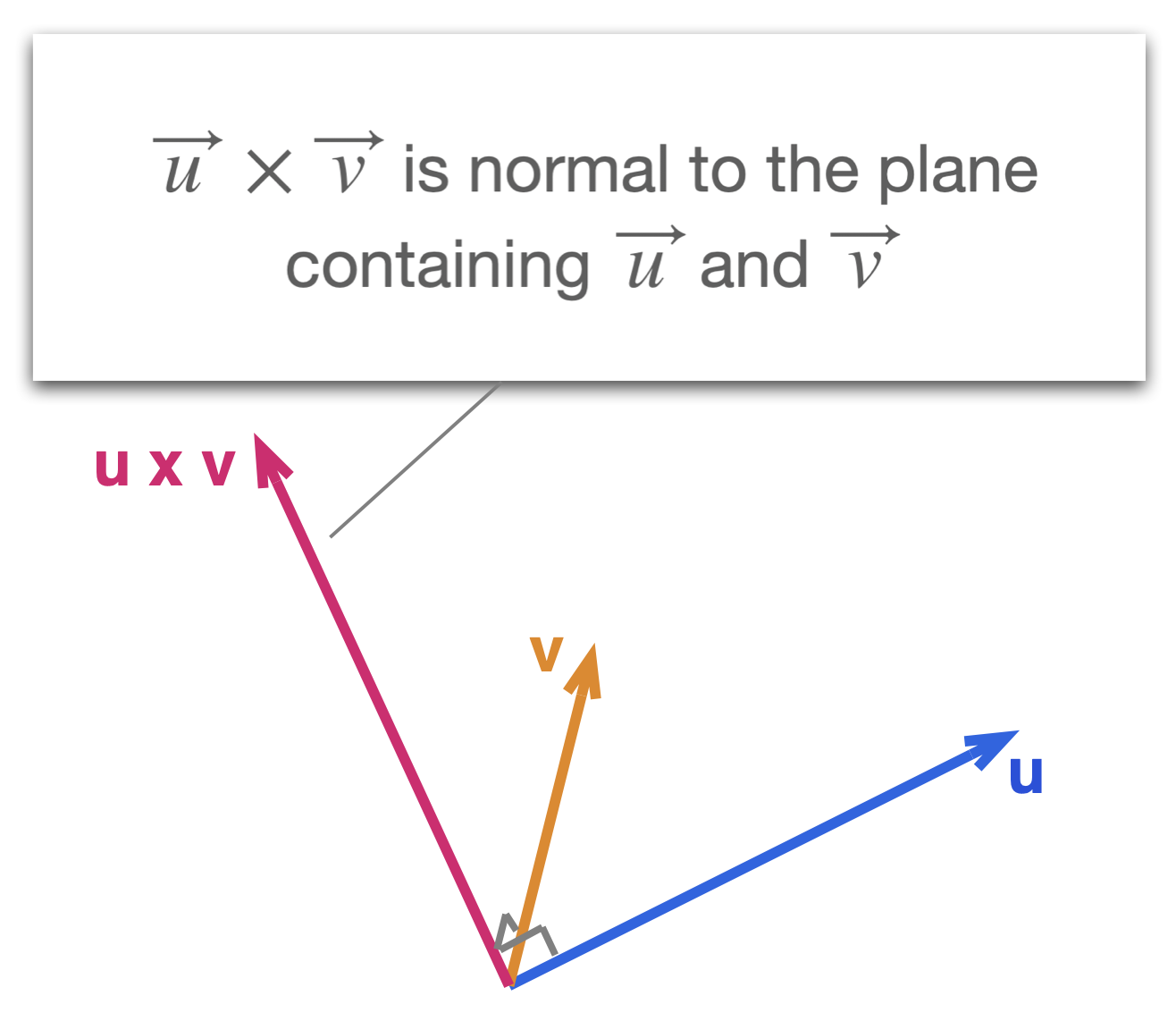
In fact, the cross product of two vectors \(\vec{u}\) and \(\vec{v}\) is a "new" vector that is perpendicular to both \(\vec{u}\) and \(\vec{v}\), we say that \(\vec{u}\times \vec{v}\) is normal to the plane containing \(\vec{u}\) and \(\vec{v}\).
How to Calculate the Cross Product
To calculate the vector product, or cross product, of two vectors we use either one of the following two options:
- Option 1: use the Formula (learn it off by heart)
- Option 2: use Matrix Algebra (recommended method)
Option 1 - The Formula: Vector Product \(\vec{u}\times \vec{v}\)
Given two vectors \(\vec{u} = \begin{pmatrix}u_1 \\ u_2 \\ u_3 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix}v_1 \\ v_2 \\ v_3 \end{pmatrix}\), the vector product, or cross product, \(\vec{u}\times \vec{v}\) can be calculated using the following formula: \[\vec{u} \times \vec{v} = \begin{pmatrix}u_2v_3 - v_2u_3\end{pmatrix} \vec{i} - \begin{pmatrix}u_1v_3 -v_1u_3\end{pmatrix} \vec{j} + \begin{pmatrix}u_1v_2 - v_1u_2\end{pmatrix} \vec{k}\] To avoid having the subtraction between the first and second term, some math courses (such as IB AA HL Mathematics) rewrite this formula as: \[\vec{u} \times \vec{v} = \begin{pmatrix}u_2v_3 - v_2u_3\end{pmatrix} \vec{i} + \begin{pmatrix} v_1u_3 - u_1v_3\end{pmatrix} \vec{j} + \begin{pmatrix}u_1v_2 - v_1u_2\end{pmatrix} \vec{k}\] Both formula are completely equivalent.
Example
Using the formula, stated above, find the cross product, \(\vec{u}\times \vec{v}\) of \(\vec{u} = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} 4 \\ 0 \\ 6 \end{pmatrix}\).
Solution
Using the second formula, stated above: \[\vec{u} \times \vec{v} = \begin{pmatrix}u_2v_3 - v_2u_3\end{pmatrix} \vec{i} + \begin{pmatrix} v_1u_3 - u_1v_3\end{pmatrix} \vec{j} + \begin{pmatrix}u_1v_2 - v_1u_2\end{pmatrix} \vec{k}\] With \(u_1 = 1\), \(u_2 = -3\), \(u_3 = 2\), \(v_1 = 4\), \(v_2 = 0\) and \(v_3 = 6\), we find: \[\begin{aligned} \vec{u}\times \vec{v} & = \begin{pmatrix}-3 \times 6 - 0 \times 2 \end{pmatrix}\vec{i} + \begin{pmatrix}4 \times 2 - 1 \times 6 \end{pmatrix}\vec{j} + \begin{pmatrix}1 \times 0 - 4 \times (-3)\end{pmatrix} \vec{k} \\ & = \begin{pmatrix}-18 -0\end{pmatrix}\vec{i} + \begin{pmatrix}8 - 6 \end{pmatrix} \vec{j} + \begin{pmatrix}0+12\end{pmatrix}\vec{k} \\ \vec{u}\times \vec{v} & = -18 \vec{i} + 2 \vec{j} + 12 \vec{k} \end{aligned} \]
Option 2: Matrix Algebra - Determinant of a 3 by 3 Matrix (recommended)
Given two vectors \(\vec{u} = \begin{pmatrix}u_1 \\ u_2 \\ u_3 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix}v_1 \\ v_2 \\ v_3 \end{pmatrix}\), the vector product, or cross product, \(\vec{u}\times \vec{v}\) equals to the following: \[ \vec{u}\times \vec{v} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \end{vmatrix}\] Notice that:
- the components in the first row consist of the unit base vectors \(\vec{i}\), \(\vec{j}\) and \(\vec{k}\) (this will always be the first row),
- the second row is the first vector in the product \(\vec{u}\times \vec{v}\), so in this case \(\vec{u}\),
- the third row is the second vector in the product \(\vec{u}\times \vec{v}\), so in this case \(\vec{v}\).
Tutorial: Cross Product - Determinant Method
Given the two vectors \(\vec{a} = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 5 \\ 0 \\ 4 \end{pmatrix}\), we learn how to calculate the cross product, \(\vec{a}\times \vec{b}\), using Matrix Algebra.
Example
Given \(\vec{u} = \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix}\), calculate their cross product \(\vec{u}\times \vec{v}\).
Solution
Using the method we just saw, we can state: \[\begin{aligned} \vec{u} \times \vec{v} & = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 2 & 1 & -3 \\ 4 & 0 & 5 \end{vmatrix} \\ & = \vec{i} \begin{vmatrix} 1 & -3 \\ 0 & 5 \end{vmatrix} - \vec{j} \begin{vmatrix} 2 & -3 \\ 4 & 5\end{vmatrix} + \vec{k} \begin{vmatrix} 2 & 1 \\ 4 & 0 \end{vmatrix} \\ & = \vec{i} \begin{pmatrix} 1 \times 5 - 0 \times (-3)\end{pmatrix} - \vec{j} \begin{pmatrix} 2\times 5 - 4 \times (-3) \end{pmatrix} + \vec{k} \begin{pmatrix} 2\times 0 - 4 \times 1 \end{pmatrix} \\ & = \vec{i}\begin{pmatrix} 5 - 0\end{pmatrix} - \vec{j} \begin{pmatrix} 10 - (-12)\end{pmatrix} + \vec{k} \begin{pmatrix} 0 - 4 \end{pmatrix} \\ & = \vec{i} \begin{pmatrix} 5 \end{pmatrix} - \vec{j}\begin{pmatrix} 10+12 \end{pmatrix} + \vec{k} \begin{pmatrix} - 4 \end{pmatrix} \\ \vec{u} \times \vec{v} & = 5 \vec{i} - 22 \vec{j} - 4 \vec{k} \end{aligned}\] That's our final answer, we can now state that \(\vec{u} \times \vec{v} = 5 \vec{i} - 22 \vec{j} - 4 \vec{k} \).
Exercise 1
- Find \(\vec{a} \times \vec{b}\), given \(\vec{a} = \begin{pmatrix}2 \\ 3 \\ 4 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 5 \\ -2 \\ 1 \end{pmatrix}\).
- Find \(\vec{c}\times \vec{d}\), given \(\vec{c} = 3 \vec{i} + 5 \vec{j} - \vec{k}\) and \(\vec{d} = \vec{i} -4 \vec{j} +2 \vec{k}\).
- Find \(\vec{u}\times \vec{v}\), given \(\vec{u} = 6 \vec{i} - 3 \vec{k}\) and \(\vec{v} = -2 \vec{i} + \vec{j} + 5 \vec{k}\).
- Find \(\vec{a} \times \vec{b}\), given \(\vec{a} = \begin{pmatrix}-2 \\ 0 \\ 6 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 4 \\ 1 \\ 3 \end{pmatrix}\).
- Find \(\vec{m}\times \vec{n}\), given \(\vec{m} = -3\vec{i} + 5 \vec{j} - \vec{k}\) and \(\vec{n} = 4\vec{j} + 7 \vec{k}\).
- Find \(\vec{u}\times \vec{v}\), given \(\vec{u} = \begin{pmatrix}8 \\ - 1 \\ -2 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix}-3 \\ - 2 \\ -4 \end{pmatrix}\).
- Find \(\vec{a}\times \vec{b}\), given \(\vec{a} = 3 \vec{i} - 2 \vec{j}\) and \(\vec{b} = 5 \vec{i} + \vec{j}\).
- Find \(\vec{c}\times \vec{d}\), given \(\vec{c} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}\) and \(\vec{d} = \begin{pmatrix} 0 \\ 3 \\ 5 \end{pmatrix}\).
AREAS OF PARALLELOGRAMS & TRIANGLES
The vector product, or cross product, of two vectors can be used to calculate the area of a parallelogram as well as the area of a triangle.
AREA of a PARALLELOGRAM
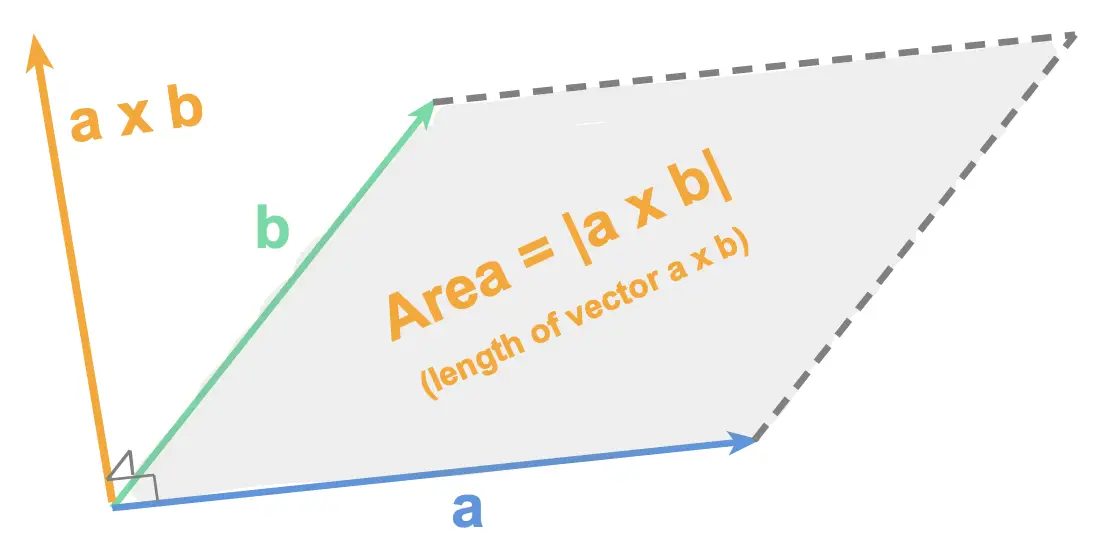
Given a parallelogram, whose sides are defined by two vectors \(\vec{a}\) and \(\vec{b}\), its area is given by: \[\text{Area} = \begin{vmatrix} \vec{a}\times \vec{b}\end{vmatrix}\] that is: the area of the parallelogram is equal to the magnitude of the cross product.
Note : the area of the parallelogram is equal to the length of the vector \(\vec{a}\times \vec{b}\):
Example
A parallelogram has sides lengths defined by the vectors \(\vec{a} = \begin{pmatrix} 6 \\ -1 \\ 3 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 1 \\ 5 \\ 4 \end{pmatrix}\).
Find this parallelogram's area.
Solution
Using the formula, stated above, we can write: \[\text{Area} = \begin{vmatrix} \vec{a}\times \vec{b}\end{vmatrix}\] Where: \[\begin{aligned} \vec{a}\times \vec{b} & = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 6 & -1 & 3 \\ 1 & 5 & 4 \end{vmatrix} \\ & = \vec{i} \begin{vmatrix} - 1 & 3 \\ 5 & 4 \end{vmatrix} - \vec{j} \begin{vmatrix} 6 & 3 \\ 1 & 4 \end{vmatrix} + \vec{k} \begin{vmatrix} 6 & -1 \\ 1 & 5 \end{vmatrix} \\ & = \vec{i} \begin{pmatrix} -1 \times 4 - 5 \times 3 \end{pmatrix} - \vec{j} \begin{pmatrix} 6 \times 4 - 1 \times 3 \end{pmatrix} + \vec{k} \begin{pmatrix} 6 \times 5 - 1 \times (-1)\end{pmatrix} \\ & = \vec{i} \begin{pmatrix} - 4 - 15 \end{pmatrix} - \vec{j} \begin{pmatrix} 24 - 3 \end{pmatrix} + \vec{k} \begin{pmatrix} 30 - (-1) \end{pmatrix} \\ & = \vec{i}(-19) - \vec{j}(21) + \vec{k}(31)\\ \vec{a}\times \vec{b} & = - 19\vec{i} - 21 \vec{j} + 31 \vec{k} \end{aligned}\] The parallelogram's area is therefore: \[\begin{aligned} \text{Area} & = \begin{vmatrix} \vec{a}\times \vec{b}\end{vmatrix} \\ & = \sqrt{(-19)^2 + (-21)^2 + 31^2} \\ & = \sqrt{1763} \\ \text{Area} & = 42.0 \quad \text{(3 s.f.)} \end{aligned}\] Rounding the answer to 3 significant figures, the area is \(42.0\) units of area.
AREA of a TRIANGLE
Given a triangle, whose sides are defined by two vectors \(\vec{a}\) and \(\vec{b}\), its area is given by: \[\text{Area} = \frac{1}{2} \begin{vmatrix} \vec{a}\times \vec{b}\end{vmatrix}\] Note : this is half of the area of the parallelogram whose sides are \(vec{a}\) and \(\vec{b}\).
Example
A triangle has two sides defined by the vectors \(\vec{a} = \begin{pmatrix} -1 \\ 7 \\ 1 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 1 \\ 4 \\ 3 \end{pmatrix}\).
Find this triangle's area.
Solution
Using the formula, stated above, we can write: \[\text{Area} = \frac{1}{2}\begin{vmatrix} \vec{a}\times \vec{b}\end{vmatrix}\] Where: \[\begin{aligned} \vec{a}\times \vec{b} & = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 6 & -1 & 7 \\ 1 & 4 & 3 \end{vmatrix} \\ & = \vec{i} \begin{vmatrix} 7 & 1 \\ 4 & 3 \end{vmatrix} - \vec{j} \begin{vmatrix} -1 & 1 \\ 1 & 3 \end{vmatrix} + \vec{k} \begin{vmatrix} -1 & 7 \\ 1 & 4 \end{vmatrix} \\ & = \vec{i} \begin{pmatrix} 7 \times 3 - 4 \times 1 \end{pmatrix} - \vec{j} \begin{pmatrix} -1\times 3 - 1\times 1 \end{pmatrix} + \vec{k} \begin{pmatrix} -1 \times 4 - 1 \times 7 \end{pmatrix} \\ & = \vec{i} \begin{pmatrix} 21 - 4 \end{pmatrix} - \vec{j} \begin{pmatrix} -3 - 1 \end{pmatrix} + \vec{k} \begin{pmatrix} -4 - 7 \end{pmatrix} \\ & = \vec{i}(17) - \vec{j}(-4) + \vec{k}(-11)\\ \vec{a}\times \vec{b} & = 17\vec{i} +4 \vec{j} -11 \vec{k} \end{aligned}\] The triangle's area is therefore: \[\begin{aligned} \text{Area} & = \frac{1}{2}\begin{vmatrix} \vec{a}\times \vec{b}\end{vmatrix} \\ & = \sqrt{17^2 + 4^2 + (-11)^2} \\ & = \sqrt{426} \\ \text{Area} & = 20.6 \quad \text{(3 s.f.)} \end{aligned}\] Rounding the answer to 3 significant figures, the area is \(20.6\) units of area.
Exercise 2 (Exam Style Questions)
- The vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) satisfy the equation \(\vec{a}+\vec{b} + \vec{c} = \vec{0}\). Show that \(\vec{a}\times \vec{b} = \vec{b}\times \vec{c} = \vec{c}\times \vec{a}\).
Scan this QR-Code with your phone/tablet and view this page on your preferred device.
 Subscribe to Our Channel
Subscribe to Our Channel
Subscribe Now and view all of our playlists & tutorials.