RadfordMathematics.com

Scalar Product - Dot Product - Vectors

(Vector Product of Two Vectors)

The dot product, also called scalar product of two vectors is one of the two ways we learn how to multiply two vectors together, the other way being the cross product, also called vector product.

When we multiply two vectors using the dot product we obtain a scalar (a number, not another vector!.

Notation

Given two vectors \(\vec{u}\) and \(\vec{v}\) we refer to the scalar product by writing:

\[\vec{u}\bullet \vec{v}\]

In other words by writing a dot between the two vectors, which explains why we also call it the dot product.

Scalar Product: using the components of the vectors

2D Vectors

Given two vectors \(\vec{u} = \begin{pmatrix} u_1 \\ u_2 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}\) their scalar product is: \[\vec{u} \bullet \vec{v} = u_1v_1 + u_2v_2 \]

3D Vectors

Given two vectors \(\vec{u} = \begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix}\) their scalar product is: \[\vec{u} \bullet \vec{v} = u_1v_1 + u_2v_2 + u_3v_3 \]

Tutorial: How to Calculate the Scalar Product

In this tutorial we learn how to calculate the scalar product of \(2\) vectors, using their components. We do this for both 2D and 3D vectors.

Example (2D Vectors)

Given \(\vec{a} = \begin{pmatrix} 2 \\ - 5 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 1 \\ -3 \end{pmatrix}\), we can calculate their scalar product \(\vec{a}\bullet \vec{b}\) as follows: \[\begin{aligned} \vec{a}\bullet \vec{b} & = 2 \times 1 + (-5)\times (-3) \\ & = 2 + 15 \\ \vec{a}\bullet \vec{b} & = 17 \end{aligned}\]

Example (3D Vectors)

Given \(\vec{u} = \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix}\), we can calculate their cross product \(\vec{u}\bullet \vec{v}\) as follows: \[\begin{aligned} \vec{u} \bullet \vec{v} & = 2\times 4 + 1\times 0 + (-3)\times 5 \\ & = 8 + 0 - 15 \\ \vec{u} \bullet \vec{v} & = -7 \end{aligned}\]

Scalar Product: using the magnitudes and angle

Given two vectors \(\vec{u}\) and \(\vec{v}\), in 2D or in 3D, their scalar product (or dot product) can be calculated using the formula: \[\vec{u} \bullet \vec{v} = \begin{vmatrix}\vec{u} \end{vmatrix}.\begin{vmatrix}\vec{v} \end{vmatrix}cos \theta\] where \(\theta \) is the angle between \(\vec{u}\) and \(\vec{v}\)

Example

Given two vectors \(\vec{a}\) and \(\vec{b}\) such that \(\begin{vmatrix} \vec{a}\end{vmatrix} = 4\), \(\begin{vmatrix} \vec{b}\end{vmatrix} = 5\) and the angle between them is \(\theta = 60^{\circ}\).

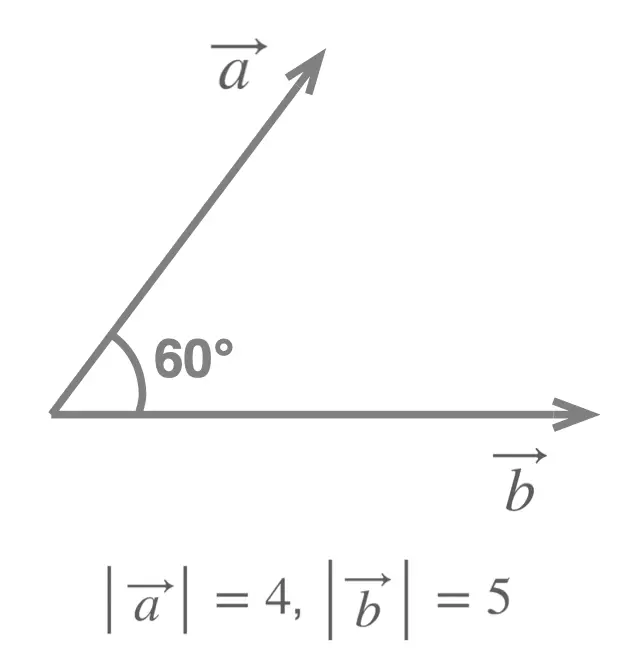The scenario we're dealing with is illustrated here. Using the formula we just saw, we can state: \[\begin{aligned} \vec{a} \cdot \vec{b} &= \begin{vmatrix} \vec{a}\end{vmatrix}. \begin{vmatrix} \vec{b}\end{vmatrix} \times cos \theta \\ & = 4\times 5 \times cos\begin{pmatrix}60^{\circ} \end{pmatrix} \\ & = 20\times 0.5 \\ \vec{a}\cdot {b} & = 10 \end{aligned} \] The scalar product of these two vectors equals \(10\).

The Role of the interior angle \(\theta \)

The angle \(\theta \) between two vectors \(\vec{u}\) and \(\vec{v}\) plays an important role on the sign of the dot product.

This is due to the fact that \(cos \theta \) changes from positive to zero to negative as \(\theta \) goes from acute, to right angle, to obtuse.

Looking at the formula \(\vec{u} \bullet \vec{v} = \begin{vmatrix}\vec{u} \end{vmatrix}.\begin{vmatrix}\vec{v} \end{vmatrix}cos \theta\) it is clear that the magnitudes \(\begin{vmatrix} \vec{u} \end{vmatrix}\) and \(\begin{vmatrix} \vec{u} \end{vmatrix}\) are always positive so \(cos \theta \) and therefore \(\theta \) is the parameter that dictaes the sign of the result.

The 3 scenarios that must be known are shown here:

When \(\theta \) is Acute

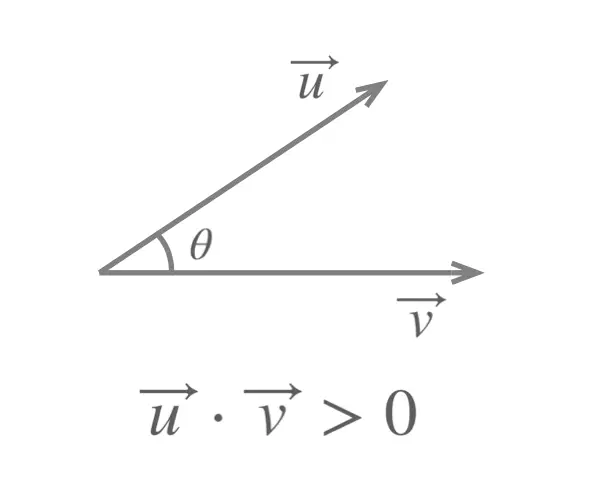
When the angle \(\theta \) between the vectors \(\vec{u}\) and \(\vec{v}\) is acute the dot product is positive: \[\vec{u} \cdot \vec{v} > 0\]

When \(\theta \) is Obtuse

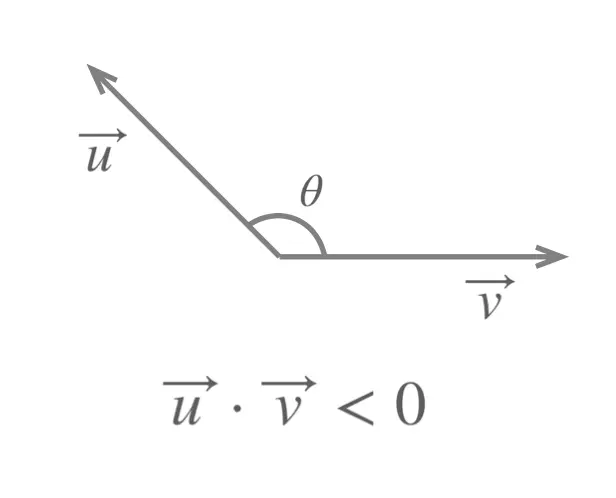
When the angle \(\theta \) between the vectors \(\vec{u}\) and \(\vec{v}\) is obtuse the dot product is negative: \[\vec{u} \cdot \vec{v} < 0\]

When \(\theta = 90^{\circ }\)

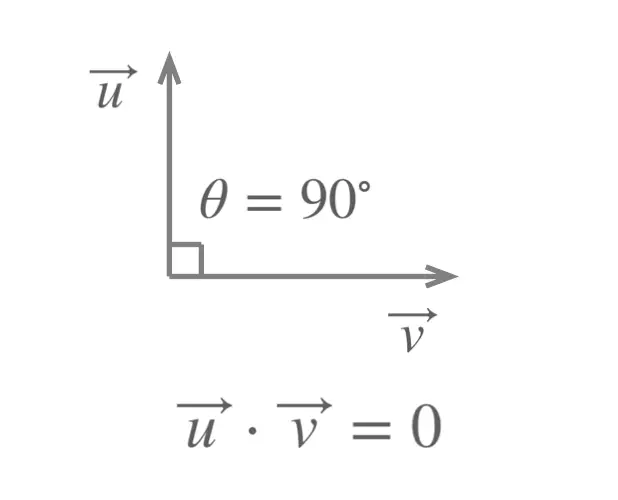
When the angle \(\theta \) between the vectors \(\vec{u}\) and \(\vec{v}\) is a right angle the dot product is equal to zero: \[\vec{u} \cdot \vec{v} = 0\]

TEST for PERPENDICULAR VECTORS

Given two vectors \(\vec{u}\) and \(\vec{v}\) (in 2D or 3D) they are perpendicular if and only if: \[\vec{u} \cdot \vec{v} = 0\]

This provides with a very useful way for checking whether two vectors are perpendicular.

Example

State whether the following pairs of vectors are perpendicular:

  1. \(\vec{u} = \begin{pmatrix} 3 \\ -2 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix}-4 \\ -6\end{pmatrix}\)
  2. \(\vec{a} = \begin{pmatrix}-5 \\ 2 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix}1 \\ 3 \end{pmatrix}\)
  3. \(\vec{a}= \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix}4 \\ -2 \\ -3\end{pmatrix}\)
  4. \(\vec{u} = \begin{pmatrix}2 \\ - 1 \\ 5 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix}-3 \\ 4 \\ 2 \end{pmatrix}\)

SEE SOLUTIONS +

  1. We find: \[\begin{aligned} \vec{u} \cdot \vec{v} & = \begin{pmatrix}3 \\ -2 \end{pmatrix} \cdot \begin{pmatrix}-4 \\ -6 \end{pmatrix}\\ & = 3\times (-4) + (-2)\times (-6) \\ & = -12 + 12 \\ \vec{u} \cdot \vec{v} & = 0 \end{aligned}\] Since \(\vec{u} \cdot \vec{v} = 0\) these two are perpendicular.
  2. We find: \[\begin{aligned} \vec{a} \cdot \vec{b} & = \begin{pmatrix} -5 \\ 2 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 3 \end{pmatrix} \\ & = -5\times 1 + 2 \times 3 \\ & = -5 + 6 \\ \vec{a} \cdot \vec{b} & = 1 \end{aligned}\] Since \(\vec{a} \cdot \vec{b} \neq 0\) they are not perpendicular.
  3. We find: \[\begin{aligned} \vec{a}\cdot \vec{b} & = \begin{pmatrix} 1 \\ 3 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ -2 \\ -3 \end{pmatrix} \\ & = 2\times 4 + 3\times (-2) + 1 \times (-3) \\ & = 8 + (-6) + (-3) \\ \vec{a}\cdot \vec{b} & = -1 \end{aligned}\] Since \(\vec{a}\cdot \vec{b} \neq 0\) vectors \(\vec{a}\) and \(\vec{b}\) are not perpendicular.
  4. We find: \[\begin{aligned} \vec{u} \cdot \vec{v} & = \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix} \cdot \begin{pmatrix} -3 \\ 4 \\ 2 \end{pmatrix} \\ & = 2\times (-3) + (-1)\times 4 + 5\times 2 \\ & = -6 + (-4) + 10 \\ & = -6 - 4 + 10 \\ \vec{u} \cdot \vec{v} & = 0 \end{aligned}\] Since \(\vec{u} \cdot \vec{v} =0\) these two vectors are perpendicular.

Tutorial: Exam Style Question

We work through a typical exam style question, seen several times in exams (although with different numbers).

Given the vectors \(\vec{u} = \begin{pmatrix} 0 \\ 5 \\ q \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} 0 \\ 10 \\ 14 \end{pmatrix}\) find the value of \(q\) for which \(\vec{u}\) and \(\vec{v}\) are:

  1. Parallel
  2. Perpendicular

Properties of the Scalar Product

For any vectors such as \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\)

  • The scalar product is commutative: \(\vec{u}\bullet \vec{v} = \vec{v}\bullet \vec{u}\)
  • The scalar product follows the "usual" laws of distributivity \(\vec{u}\bullet \begin{pmatrix} \vec{v} + \vec{v}\end{pmatrix} = \vec{u}\bullet \vec{v} + \vec{u}\bullet \vec{w}\)
  • \(\vec{u} \bullet \vec{u} = \begin{vmatrix} \vec{u} \end{vmatrix}^2\)
  • Given a vector \(\vec{u}\) and a scalar \(k\in\mathbb{R}\): \(\begin{vmatrix} k.\vec{u}\end{vmatrix} = \begin{vmatrix} k\end{vmatrix}.\begin{vmatrix} \vec{u}\end{vmatrix}\)

Example 1

Given the two vectors \(\vec{a} = \begin{pmatrix}1 \\ 4 \\ -3\end{pmatrix}\) and \(\vec{b} = \begin{pmatrix}2 \\ 7 \\ 5\end{pmatrix}\), we can show that \(\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \):

\[\begin{aligned} \vec{a} \cdot \vec{b} & = 1 \times 2 + 4 \times 7 + (-3)\times 5 \\ & = 2 + 28 +(-15) \\ & = 30 - 15 \\ \vec{a} \cdot \vec{b} & = 15 \end{aligned}\]
\[\begin{aligned} \vec{b} \cdot \vec{a} & = 2 \times 1 + 7 \times 4 + 5 \times (-3) \\ & = 2 + 28 +(-15) \\ & = 30 - 15 \\ \vec{b} \cdot \vec{a} & = 15 \end{aligned}\]
we can clearly see that \(\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}\).

Example 2

Given the two vectors \(\vec{u} = \begin{pmatrix} 2 \\ 6 \\ 3\end{pmatrix}\), \( \vec{v} = \begin{pmatrix} 5 \\ 1 \\ -3\end{pmatrix} \) and \( \vec{w} = \begin{pmatrix} 4 \\ -1 \\ 2\end{pmatrix} \) we can verify that \(\vec{u} \cdot \begin{pmatrix} \vec{v} + \vec{w} \end{pmatrix}\) as follows:

\[\begin{aligned} \vec{u} \cdot \begin{pmatrix} \vec{v} + \vec{w} \end{pmatrix} & = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w} \\ & = \begin{pmatrix} 2 \\ 6 \\ 3\end{pmatrix} \cdot \begin{pmatrix} 5 \\ 1 \\ -3\end{pmatrix} + \begin{pmatrix} 2 \\ 6 \\ 3\end{pmatrix} \cdot \begin{pmatrix} 4 \\ -1 \\ 2\end{pmatrix} \\ & = \underbrace{2 \times 5 + 6 \times 1 +3 \times (-3)}_{\vec{u}\cdot \vec{v}} + \underbrace{2\times 4 + 6 \times (-1) + 3\times 2}_{\vec{u}\cdot \vec{w}} \\ & = 10 + 6 + (-9) + 8 + (-6)+ 6 \\ & = 10 + 6 - 9 + 8 - 6 + 6 \\ & = 16 - 9 + 8 - 6 + 6 \\ & = 7 + 8 - 6 + 6 \\ & = 15 - 6 + 6 \\ & = 9 + 6 \\ \vec{u} \cdot \begin{pmatrix} \vec{v} + \vec{w} \end{pmatrix} & = 15 \end{aligned}\]
\[\begin{aligned} \vec{u} \cdot \begin{pmatrix} \vec{v} + \vec{w} \end{pmatrix} & = \begin{pmatrix} 2 \\ 6 \\ 3\end{pmatrix} \cdot \begin{pmatrix} \begin{pmatrix} 5 \\ 1 \\ -3\end{pmatrix} + \begin{pmatrix} 4 \\ -1 \\ 2\end{pmatrix} \end{pmatrix} \\ & = \begin{pmatrix} 2 \\ 6 \\ 3\end{pmatrix} \cdot \begin{pmatrix} \begin{pmatrix} 5+4 \\ 1 + (-1) \\ -3 + 2 \end{pmatrix} \end{pmatrix} \\ & = \begin{pmatrix} 2 \\ 6 \\ 3\end{pmatrix} \cdot \begin{pmatrix} 9 \\ 0 \\ -1 \end{pmatrix} \\ & = 2\times 9 + 6 \times 0 + 3 \times (-1) \\ & = 18 + 0 + (-3) \\ & = 18 - 3 \\ \vec{u} \cdot \begin{pmatrix} \vec{v} + \vec{w} \end{pmatrix} & = 15 \end{aligned}\]
We can see that both results are equal and that the scalar product obeys the "usual" laws of distibutivity.

Exercise 1

  1. Calculate the dot product of each of the following pairs of vectors:
    1. \(\vec{a} = \begin{pmatrix} -2 \\ 1 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 3 \\ 7 \end{pmatrix}\)
    2. \(\vec{u} = 3 \vec{i} - 2 \vec{j} + \vec{k}\) and \(\vec{v} = - \vec{i} + 4 \vec{j} + 2 \vec{k}\)
    3. \(\vec{c} = \begin{pmatrix} 2 \\ 0 \\ - 5\end{pmatrix}\) and \(\vec{d} = \begin{pmatrix} 1 \\ - 3 \\ 4 \end{pmatrix}\)
  2. Given the vectors \(\vec{a} = \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix}1 \\ -2 \\ p \end{pmatrix}\), find the value of \(p\) for which \(\vec{a}\) and \(\vec{b}\) are perpendicular.
  3. Given the vectors \(\vec{u} = \begin{pmatrix} 0 \\ 5 \\ q \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} 0 \\ 10 \\ 14 \end{pmatrix}\), find the value of \(q\) for which \(\vec{u}\) and \(\vec{v}\) are:
    1. parallel
    2. perpendicular
  4. Show that triangle ABC, where the vertices \(A\), \(B\) and \(C\) have coordinates \(A(0,-3,9)\), \(B(5,-10,10)\) and \(C(2,-4,6)\) is right angled at \(C\).
  5. Given \(\vec{u} = \begin{pmatrix} 2k \\ - 1 \\ 1 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} k \\ k \\ -1 \end{pmatrix}\) are perpendicular and \(k >0\), find the value of \(k\).

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.