RadfordMathematics.com

Vectors - Addition, Subtraction & Multiplication by a Scalar

(Operations with Vectors - Component and Graphical Methods)

In this section we start learning about operations with vectors. In particular, we learn how to add, and subtract, with vectors as well as how to multiply a vector by a scalar. We start by watching a tutorial, beneath which we'll find the lesson notes that go with it. Finally we'll work through an exercise.

"Simple" Operations with Vectors

Given the two vectors \(\vec{a} = \begin{pmatrix} 1 \\ 5 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 6 \\ 3 \end{pmatrix}\), we learn add and subtract with vectors, by finding \(\vec{a}+ \vec{b}\) and \(\vec{a}- \vec{b}\). We also learn how to multiply a vector by a scalar by finding \(3.\vec{a}\).

Addition & Subtraction with Vectors

Given two vectors in component form, \(\vec{u} = \begin{pmatrix}x \\ y \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix}x' \\ y' \end{pmatrix}\), we can add them together or subtract one from the other as follows:

Addition

\[\begin{aligned} \vec{u} + \vec{v} & = \begin{pmatrix}x \\ y \end{pmatrix} + \begin{pmatrix}x' \\ y' \end{pmatrix} \\ & = \begin{pmatrix} x + x' \\ y + y'\end{pmatrix} \end{aligned}\]

Subtraction

\[\begin{aligned} \vec{u} - \vec{v} & = \begin{pmatrix}x \\ y \end{pmatrix} - \begin{pmatrix}x' \\ y' \end{pmatrix} \\ & = \begin{pmatrix} x - x' \\ y - y'\end{pmatrix} \end{aligned}\]

Example 1

Given the two vectors \(\vec{a} = \begin{pmatrix}1 \\ 4 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix}2 \\ 7 \end{pmatrix}\), we calculate \(\vec{a}+ \vec{b}\) as follows: \[\begin{aligned} \vec{a}+ \vec{b} & = \begin{pmatrix} 1 \\ 4 \end{pmatrix} + \begin{pmatrix}2 \\ 7 \end{pmatrix} \\ & = \begin{pmatrix} 1 + 2 \\ 4 + 7 \end{pmatrix} \\ \vec{a}+ \vec{b} & = \begin{pmatrix} 3 \\ 11 \end{pmatrix} \end{aligned}\]

Example 2

Given the two vectors \(\vec{u} = \begin{pmatrix} 2 \\ 6 \end{pmatrix}\) and \( \vec{v} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} \) we can subract \(\vec{v}\) from \(\vec{u}\) as follows: \[\begin{aligned} \vec{u} - \vec{v} & = \begin{pmatrix} 2 \\ 6 \end{pmatrix} - \begin{pmatrix} 5 \\ 1 \end{pmatrix} \\ & = \begin{pmatrix} 2 - 5 \\ 6 - 1 \end{pmatrix} \\ \vec{u} - \vec{v} & = \begin{pmatrix} - 3 \\ 5 \end{pmatrix} \end{aligned}\]

GRAPHICAL ADDITION & SUBTRACTION

ADDITION

To add two vectors graphically, we'll use either-one of the following two methods:

  • The Tail-to-Head Method
  • The Parallelogram Rule

Tutorial : Graphical Addition of Vectors

The two methods we learn about for adding vectors graohically are shown/explained here.

METHOD 1: TAIL-to-HEAD METHOD for ADDING VECTORS

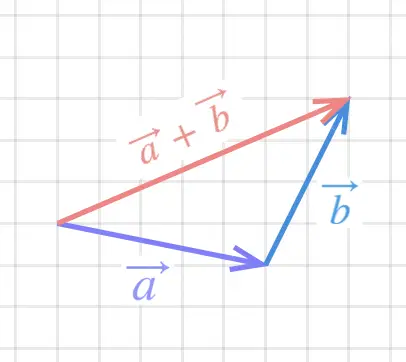Given two vectors, such as \(\vec{a}\) and \(\vec{b}\) shown here, to add these two vectors using the Tail-to-Head Method we can follow 3 steps:

  • Step 1: draw vector \(\vec{a}\)
  • Step 2: Starting from the head of vector \(\vec{a}\), draw vector \(\vec{b}\).
  • Step 3: Draw the resultant vector, \(\vec{a}+\vec{b}\), going from the tail of \(\vec{a}\) to the head of \(\vec{b}\).

Worked Example

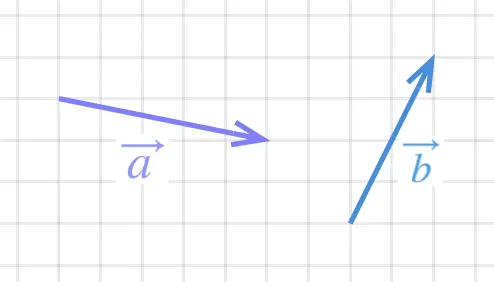Given the vectors shown here, draw the resultant vector \(\vec{a} + \vec{b}\).

Note: for this example we can find the vectors' components by reading-off the graph paper. Indeed we can see that \(\vec{a} = \begin{pmatrix} 5 \\ -1 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 2 \\ 4 \end{pmatrix}\). So, following what we learnt above, we now that: \[\vec{a}+\vec{b} = \begin{pmatrix}5 \\ -1 \end{pmatrix} + \begin{pmatrix} 2 \\ 4 \end{pmatrix}\] Which leads us to the resultant vector: \[\vec{a}+\vec{b} = \begin{pmatrix}7 \\ 3 \end{pmatrix}\] Now we can show this graphically:

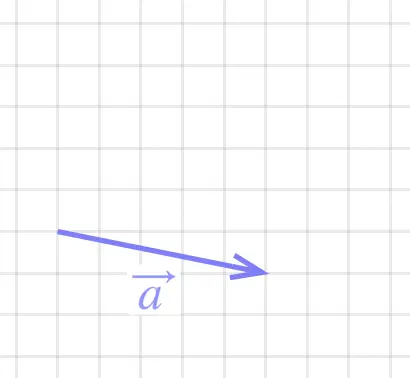
Step 1: Draw \(\vec{a}\)

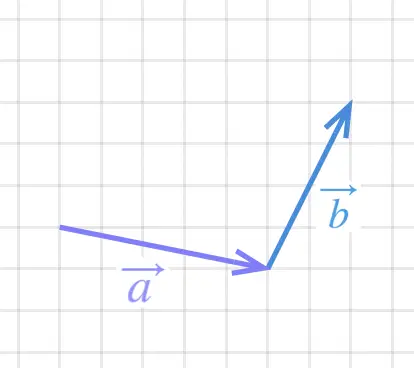
Step 2: Draw \(\vec{b}\) Starting From the Head of \(\vec{a}\)

Step 3: Draw the Resultant Vector \(\vec{a}+\vec{b}\) by joining the Tail of \(\vec{a}\) to the Head of \(\vec{b}\)

METHOD 2: The PARALLELOGRAM RULE

Given two vectors \(\vec{a}\) and \(\vec{b}\), if we draw \(\vec{a}\) and \(\vec{b}\) from the same starting point and let them form two adjacent sides of a parallelogram then the resultant vector, \(\vec{a}+\vec{b}\), is the parallelogram's diagonal that leaves the same point as \(\vec{a}\) and \(\vec{n}\).

This method is illustrated further down and summarized with the following 3 steps:

  • Step 1: draw the two vectors \(\vec{a}\) and \(\vec{b}\) from the same starting point.
  • Step 2: draw (or visualise) the parallelogram formed by the two vectors drawn in step 1.
  • Step 3: draw the resultant vector, \(\vec{a}+\vec{b}\), along the parallelogram's diagonal with the same starting point as \(\vec{a}\) and \(\vec{b}\).

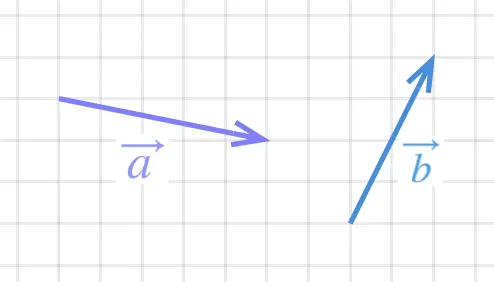Worked Example

Given the vectors shown here, use the parallelogral rule to draw the resultant vector \(\vec{a} + \vec{b}\).

Note: for the sake of comparison, we'll use the same vectors as we did for the Head-to-Tail Method.

Solution

Step 1

: draw the two vectors \(\vec{a}\) and \(\vec{b}\) from the same starting point.

Step 2

: draw (or visualise) the parallelogram formed by the two vectors drawn in step 1.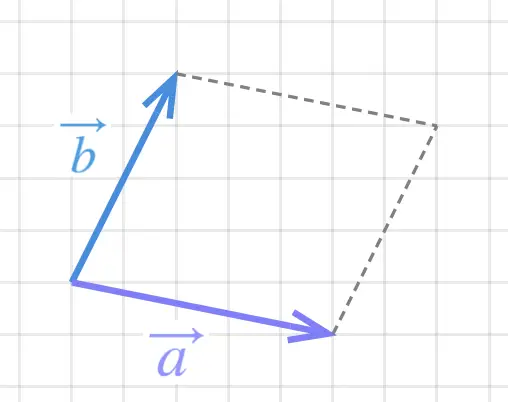

Step 3

: draw the resultant vector, \(\vec{a}+\vec{b}\), along the parallelogram's diagonal with the same starting point as \(\vec{a}\) and \(\vec{b}\).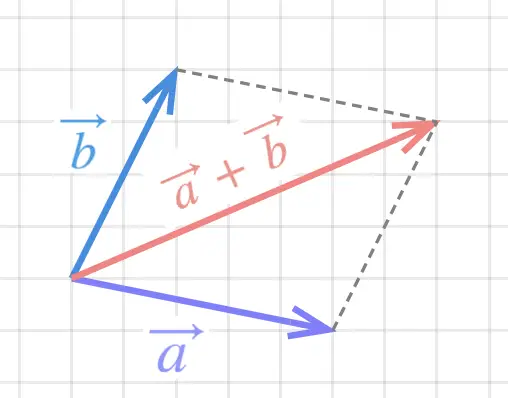

Multiplication by a Scalar (Algebraic Method)

Given a vector \(\vec{u} = \begin{pmatrix} x \\ y \end{pmatrix}\) and a scalar \(k \in \mathbb{R}\) (in this context, scalar is just another word for number). We can multiply the vector \(\vec{u}\) by \(k\), by multiplying each of its components by \(k\) as follows: \[ k.\vec{u} = k.\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} kx \\ ky \end{pmatrix} \]

Example 3

Given the vector \(\vec{u} = \begin{pmatrix} 2 \\ 5 \end{pmatrix}\) we define the vector \(3.\vec{u}\) as follows: \[\begin{aligned} 3.\vec{u} & = 3.\begin{pmatrix} 2 \\ 5 \end{pmatrix} \\ & = \begin{pmatrix} 3\times 2 \\ 3\times 5 \end{pmatrix} \\ \vec{u} & = \begin{pmatrix} 6 \\ 15 \end{pmatrix} \end{aligned} \]

Multiplication by a Scalar (Graphical Method)

Given a vector \(\vec{v}\), when we multiply this by a scalar \(k\in \mathbb{R}\), the new vector \(k.\vec{v}\) will:

  • be parallel to vector \(\vec{v}\)
  • point in a direction that depends on the sign of \(k\):
    • if \(k>0\): then \(k.\vec{v}\) will point in the same direction as \(\vec{v}\)
    • if \(k<0\): then \(k.\vec{v}\) will point in the opposite direction as \(\vec{v}\)
  • have length \(\begin{vmatrix}k\end{vmatrix} \times \text{(the length of vector \(\vec{v}\))}\) in terms of the magnitude of the vector \(\vec{v}\) that's: \(\lVert k.\vec{v} \rVert = \begin{vmatrix}k\end{vmatrix}. \lVert \vec{v} \rVert \), where \(\begin{vmatrix} k \end{vmatrix}\) is the absolute value of \(k\).

Example

Given the vector \(\vec{v} = \begin{pmatrix} 3 \\ 5 \end{pmatrix}\), the following vectors can be seen on the graph paper shown here:

  • \(2\vec{v}\)
  • \(-3\vec{v}\)
  • \(0.5\vec{v}\)

Looking at this the four vectors we notice:

  • they are all parallel, we also say the vectors are colinear
  • the vectors \(\vec{v}\), \(2\vec{v}\) and \(0.5\vec{v}\) all point in the same direction
  • the vector \(-3\vec{v}\) points in the opposite direction.
  • the vectors length's (and therefore magnitudes) are such that:
    • \(2\vec{v}\) is 2 times longer than \(\vec{v}\) so \(\lVert 2\vec{v} \rVert = 2. \lVert \vec{v} \rVert \)
    • \(-3\vec{v}\) is 3 times longer than \(\vec{v}\) so \(\lVert -3\vec{v} \rVert = 3. \lVert \vec{v} \rVert \)
    • \(0.5\vec{v}\) is half as long as \(\vec{v}\) so \(\lVert 0.5\vec{v} \rVert = 0.5 \lVert \vec{v} \rVert \)

Exercise 1

  1. Find \(\vec{a}+ \vec{b}\) where \(\vec{a} = \begin{pmatrix}1 \\ 4 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix}2 \\ 5 \end{pmatrix}\).
  2. Find \(\vec{c} - \vec{d}\) where \(\vec{c} = \begin{pmatrix}4 \\ 2 \end{pmatrix}\) and \(\vec{d} = \begin{pmatrix}1 \\ 5 \end{pmatrix}\).
  3. Find \(3\vec{u}\) where \(\vec{u} = \begin{pmatrix} -2 \\ 7 \end{pmatrix}\).
  4. Find \(2\vec{a} + \vec{b}\) where \(\vec{a} = \begin{pmatrix} -1 \\ 3 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 4 \\ 6 \end{pmatrix}\).
  5. Find \(\vec{u} - 2\vec{v}\) where \(\vec{u} = \begin{pmatrix} 5 \\ 0 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} 2 \\ -3 \end{pmatrix}\).
  6. Find \(4\vec{b} + 2\vec{c}\) where \(\vec{b} = \begin{pmatrix} 3 \\ 4 \end{pmatrix}\) and \(\vec{c} = \begin{pmatrix} -1 \\ 5 \end{pmatrix}\).
  7. Find \(-2\vec{a} + \vec{b}\) where \(\vec{a} = \begin{pmatrix} 3 \\ 7 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 6 \\ -2 \end{pmatrix}\).
  8. Find \(\vec{a} - 2\vec{b}\) where \(\vec{a} = \begin{pmatrix} 3 \\ 4 \end{pmatrix}\) and \(\vec{b} = \begin{pmatrix} 1 \\ 3 \end{pmatrix}\).
  9. Find \(4\vec{u} - 3\vec{v}\) where \(\vec{u} = \begin{pmatrix} 4 \\ 5 \end{pmatrix}\) and \(\vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\).
  10. Find \(\vec{a} + \vec{b} + \vec{c}\) where \(\vec{a} = \begin{pmatrix} -2 \\ 3 \end{pmatrix}\), \(\vec{b} = \begin{pmatrix} 4 \\ 5 \end{pmatrix}\) and \(\vec{c} = \begin{pmatrix} 6 \\ -7 \end{pmatrix}\).
  11. Find \(2\vec{u} + \vec{v} - 3\vec{w}\) where \(\vec{u} = \begin{pmatrix} 4 \\ 3 \end{pmatrix}\), \(\vec{v} = \begin{pmatrix} 0 \\ -1 \end{pmatrix}\) and \(\vec{w} = \begin{pmatrix} 2 \\ 2 \end{pmatrix}\).
  12. Find \(\vec{a} + 2\vec{b} - 3\vec{c}\) where \(\vec{a} = \begin{pmatrix} 25 \\ 22 \end{pmatrix}\), \(\vec{b} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}\) and \(\vec{c} = \begin{pmatrix} 4 \\ 5 \end{pmatrix}\).

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

Solution Without Working

  1. We find \(\vec{a}+ \vec{b} = \begin{pmatrix}3 \\ 9 \end{pmatrix}\).
  2. We find \(\vec{c} - \vec{d} = \begin{pmatrix} 3 \\ -3 \end{pmatrix}\).
  3. We find \(3\vec{u} = \begin{pmatrix} -6 \\ 21 \end{pmatrix}\).
  4. We find \(2\vec{a} + \vec{b} = \begin{pmatrix} 2 \\ 12 \end{pmatrix}\).
  5. We find \(\vec{u} - 2\vec{v} = \begin{pmatrix} 1 \\ 6 \end{pmatrix} \).
  6. We find \(4\vec{b} + 2\vec{c} = \begin{pmatrix} 10 \\ 26 \end{pmatrix}\).
  7. We find \(-2\vec{a} + \vec{b} = \begin{pmatrix} 0 \\ -16 \end{pmatrix} \).
  8. We find \(\vec{a} - 2\vec{b} = \begin{pmatrix} 1 \\ -2 \end{pmatrix}\).
  9. We find \(4\vec{u} - 3\vec{v} = \begin{pmatrix} 10 \\ 11 \end{pmatrix} \).
  10. We find \(\vec{a} + \vec{b} + \vec{c} = \begin{pmatrix} 8 \\ 1 \end{pmatrix}\).
  11. We find \(2\vec{u} + \vec{v} - 3\vec{w} = \begin{pmatrix} 2 \\ -1 \end{pmatrix}\).
  12. Find \(\vec{a} - 2\vec{b} - 3\vec{c} = \begin{pmatrix} 9 \\ 1 \end{pmatrix} \).


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.